数据结构--图 Graph

文章目录

- 1. 概念
- 2. 存储方法
- - 2.1 邻接矩阵 Adjacency Matrix
  - 2.2 邻接表 Adjacency List
- 3. 图的遍历
- - 3.1 广度优先搜索BFS（Breadth First Search）
  - 3.2 BFS代码（基于邻接表）
  - 3.3 深度优先搜索DFS（Depth First Search）
  - 3.4 DFS代码（基于邻接表）
  - 3.5 BFS代码（基于邻接矩阵）
  - 3.6 DFS代码（基于邻接矩阵）

1. 概念

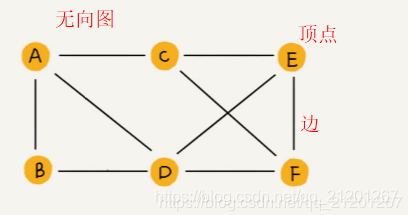
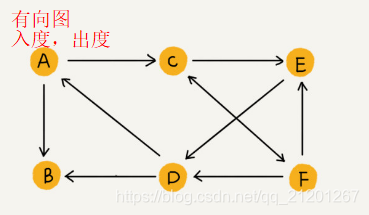
在这里插入图片描述

顶点的入度，表示有多少条边指向这个顶点；
顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点。

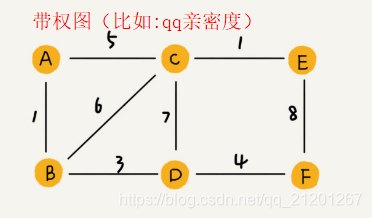
2. 存储方法

2.1 邻接矩阵 Adjacency Matrix

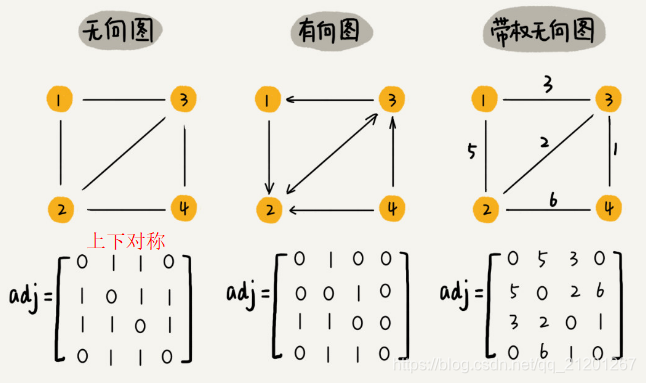
在这里插入图片描述
存储比较浪费，有的顶点很多，但是边很少（微信用户很多，每个用户的好友只百个），用邻接矩阵存储，其中大部分都是0，浪费。

邻接矩阵优点。

首先，邻接矩阵的存储方式简单、直接，因为基于数组，所以在获取两个顶点的关系时，就非常高效。
其次，用邻接矩阵存储图的另外一个好处是方便计算（矩阵运算）。

2.2 邻接表 Adjacency List

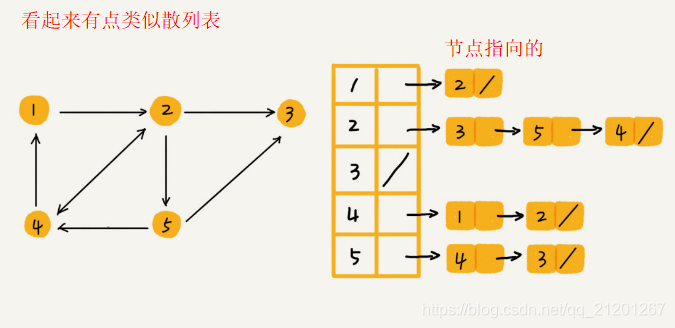
在这里插入图片描述
邻接表节省内存，但是查找起来需要遍历链表，可以将链表改造成红黑树、跳表、散列表、有序动态数组（二分查找）等。

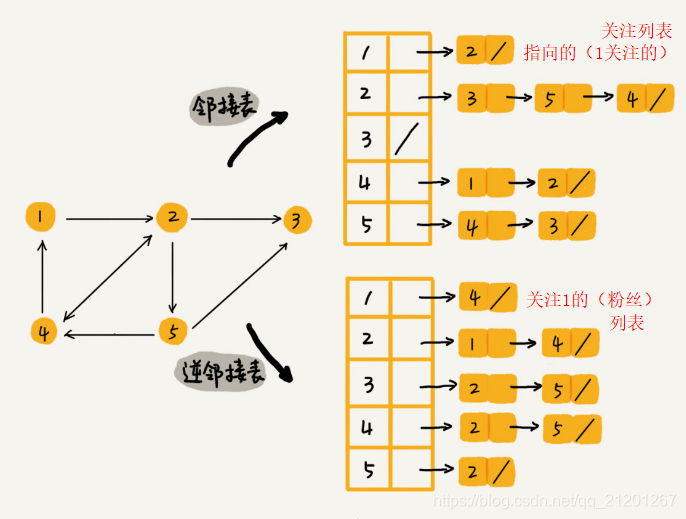
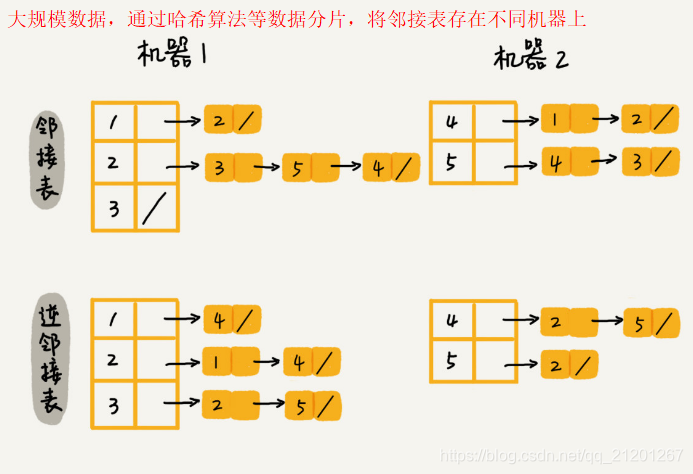
3. 图的遍历

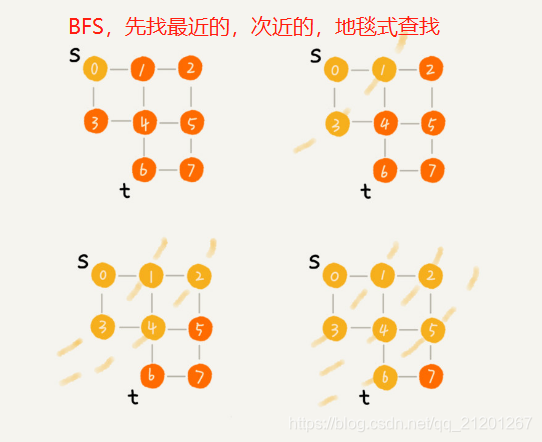
3.1 广度优先搜索BFS（Breadth First Search）

在这里插入图片描述

3.2 BFS代码（基于邻接表）

广度优先搜索找到的是最短路径

/*** @description: BFS* @author: michael ming* @date: 2019/6/4 23:05* @modified by: */
#include <list>
#include <queue>
#include <iostream>
#include <memory.h>
using namespace std;
class graph
{int v;//顶点个数list<int> *adj;//邻接表
public:graph(int numofvertex){v = numofvertex;adj = new list<int> [v];}~graph(){delete [] adj;}void insertEdge(int s, int t)   //无向图，一次存两边{s--;t--;adj[s].push_back(t);adj[t].push_back(s);}void print(){for(int i = 0; i < v; ++i){cout << "邻接表，节点 " << i << " is \n";for(auto it = adj[i].begin(); it != adj[i].end();++it){cout << *it << " ";}cout << endl;}}void bfs(int s)//从s开始遍历全部{bool *visited = new bool [v];memset(visited,false, sizeof(bool)*(v));visited[s] = true;//visited存储已经访问的节点，避免重复访问list<int> q;//q.push_back(s);list<int>::iterator it;cout << "从" << s << "开始广度搜索的结果是:" << endl;while(!q.empty()){int w = q.front();cout << w << " ";q.pop_front();for(it = adj[w].begin(); it != adj[w].end();++it){if(visited[*it]==false){visited[*it] = true;q.push_back(*it);}}}delete [] visited;}void bfs(int s, int t)//从s开始,搜索t{if(s == t)return;bool *visited = new bool [v];memset(visited,false, sizeof(bool)*(v));visited[s] = true;//visited存储已经访问的节点，避免重复访问list<int> q;q.push_back(s);int *prev = new int [v];//记录搜索的路径for(int i = 0; i < v; ++i)prev[i] = -1;list<int>::iterator it;cout << "从" << s << "开始搜索" << t << "的结果是:" << endl;while(!q.empty()){int w = q.front();q.pop_front();for(it = adj[w].begin(); it != adj[w].end();++it){if(visited[*it]==false){prev[*it] = w;//从w找到了it位置，记录下来if(*it == t){printPath(prev, s, t);//递归打印路径delete [] visited;delete [] prev;return;}visited[*it] = true;q.push_back(*it);}}}delete [] visited;delete [] prev;}void printPath(int *prev, int s, int t){if(prev[t] != -1 && t != s){printPath(prev, s, prev[t]);//递归打印路径}cout << t << " ";}
};int main()
{graph gp(8);gp.insertEdge(1,2);gp.insertEdge(2,3);gp.insertEdge(1,4);gp.insertEdge(2,5);gp.insertEdge(3,6);gp.insertEdge(4,5);gp.insertEdge(5,6);gp.insertEdge(5,7);gp.insertEdge(6,8);gp.insertEdge(7,8);gp.print();gp.bfs(7);cout << endl;gp.bfs(7,1);return 0;
}

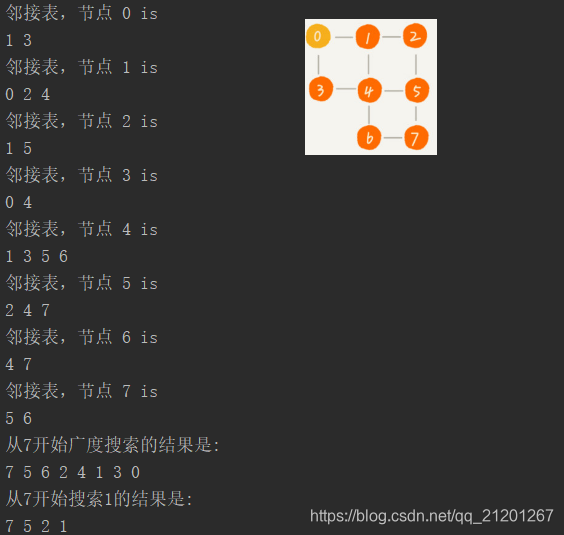
在这里插入图片描述
最坏情况，起终点很远，所有点都要进出队列，每个边也被访问一次，时间复杂度O(V+E)，对于所有顶点都是联通的，E边大于等于V-1，可简写O(E)；
空间复杂度O(V)，存储的空间不会超过顶点个数

3.3 深度优先搜索DFS（Depth First Search）

一条路走到底，发现都访问过了，还没找到，返回到上一个岔路口，继续查找。

3.4 DFS代码（基于邻接表）

void dfs_r(int s)//从s开始递归法深度搜索遍历
{cout << "从" << s << "开始深度搜索的结果是（递归）:" << endl;bool *visited = new bool [v];memset(visited,false, sizeof(bool)*(v));dfs_recu(visited, s);delete [] visited;
}
void dfs_recu(bool *visited, int s)
{list<int>::iterator it;visited[s] = true;cout << s << " ";for(it = adj[s].begin(); it != adj[s].end();++it){if(!visited[*it])dfs_recu(visited, *it);}
}
void dfs_r(int s, int t)//从s开始递归法深度遍历搜索t
{bool found = false;cout << "从" << s << "开始深度搜索" << t << "的结果是（递归）:" << endl;bool *visited = new bool [v];memset(visited,false, sizeof(bool)*(v));int *prev = new int [v];//记录搜索的路径for(int i = 0; i < v; ++i)prev[i] = -1;dfs_recu(visited, prev, found, s, t);printPath(prev, s, t);delete [] visited;delete [] prev;
}
void dfs_recu(bool *visited, int *prev, bool &found, int s, int t)
{if(found == true)//如果已经找到了，for循环剩余的不执行（优化）return;visited[s] = true;if(s == t){found = true;return;}for(auto it = adj[s].begin(); it != adj[s].end();++it){if(!visited[*it]){prev[*it] = s;dfs_recu(visited, prev, found, *it, t);}}
}
void dfs(int s)//从s开始，非递归深度遍历
{bool *visited = new bool [v];memset(visited,false, sizeof(bool)*(v));visited[s] = true;//visited存储已经访问的节点，避免重复访问stack<int> q;q.push(s);list<int>::iterator it;cout << "从" << s << "开始深度搜索的结果是（非递归）:" << endl;while(!q.empty()){int w = q.top();q.pop();if(visited[w] == true){cout << w << " ";for(it = adj[w].begin(); it != adj[w].end();++it){if(visited[*it]==false){visited[*it] = true;q.push(*it);}}}}delete [] visited;
}
void dfs(int s, int t)//从s开始，非递归深度遍历搜索t
{if(s == t)return;bool *visited = new bool [v];memset(visited,false, sizeof(bool)*(v));visited[s] = true;//visited存储已经访问的节点，避免重复访问stack<int> q;q.push(s);int *prev = new int [v];//记录搜索的路径for(int i = 0; i < v; ++i)prev[i] = -1;list<int>::iterator it;cout << "从" << s << "开始深度搜索" << t << "的结果是（非递归）:" << endl;while(!q.empty()){int w = q.top();q.pop();if(visited[w] == true){for(it = adj[w].begin(); it != adj[w].end();++it){if(visited[*it]==false){prev[*it] = w;if(*it == t){printPath(prev, s, t);//递归打印路径delete [] visited;delete [] prev;return;}visited[*it] = true;q.push(*it);}}}}delete [] visited;delete [] prev;
}

gp.dfs_r(6);    cout << endl;
gp.dfs(6);      cout << endl;
gp.dfs_r(5,3);  cout << endl;
gp.dfs(5,3);

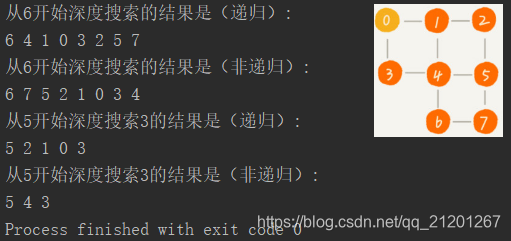
在这里插入图片描述
深度优先和广度优先搜索的时间复杂度都是O(E)，空间复杂度是 O(V)。
基于邻接表的 BFS&DFS 完整代码：https://github.com/hitskyer/course/blob/master/dataAlgorithm/chenmingming/graph/BFS_DFS.cpp

3.5 BFS代码（基于邻接矩阵）

/*** @description: 基于邻接矩阵的无向图* @author: michael ming* @date: 2019/6/11 21:50* @modified by: */
#include <iostream>
#include <queue>
#include <stack>
using namespace std;
#define MaxNum 20   //最大顶点数
#define MaxValue 65535  //最大值(标记矩阵空位)
class arrGraph  //邻接矩阵图
{
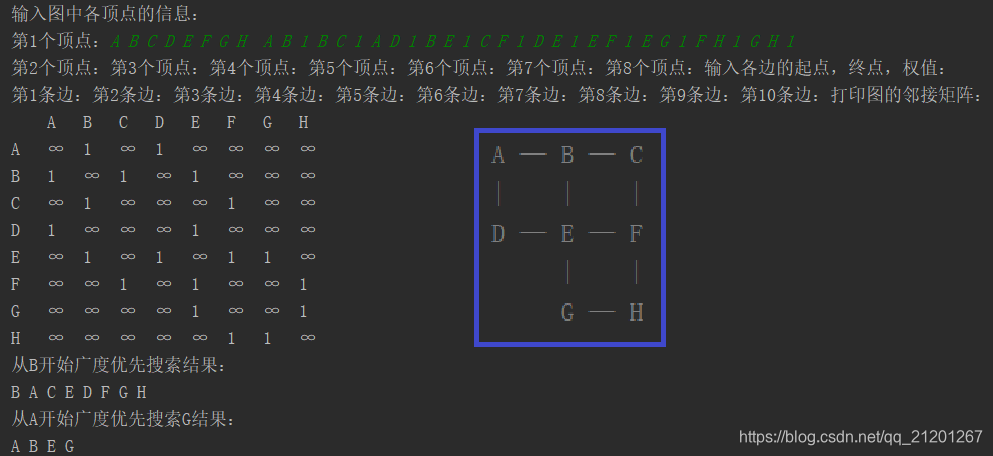
public:char vertex[MaxNum];    //顶点信息int GType;              //图的类型（0无向图，1有向图）int v;                  //顶点个数int e;                  //边数量int ew[MaxNum][MaxNum]; //边的权重int visited[MaxNum];    //访问标志arrGraph(int vertexNum, int edgeNum, int gt = 0){v = vertexNum;e = edgeNum;GType = gt;clearGraph();}void creatGraph(){int i, j, k;//循环用计数器int weight;//权重char startV, endV;//边的起始终止点cout << "输入图中各顶点的信息：" << endl;for(i = 0; i < v; ++i){cout << "第" << i+1 << "个顶点：";cin >> vertex[i];}cout << "输入各边的起点，终点，权值：" << endl;for(k = 0; k < e; ++k){cout << "第" << k+1 << "条边：";cin >> startV >> endV >> weight;for(i = 0; startV != vertex[i]; ++i);   //查找起点for(j = 0; endV != vertex[j]; ++j);     //终点ew[i][j] = weight;                      //权值，一条边 i->jif(GType == 0)ew[j][i] = weight;  //无向图，对称位置一样的权}}void clearGraph(){int i, j;for(i = 0; i < v; ++i)for(j = 0; j < v; ++j)ew[i][j] = MaxValue;    //清空矩阵（每个值置为MaxValue）}void printArrOfGraph(){int i, j;for(j = 0; j < v; ++j)cout << "\t" << vertex[j];//第1行顶点信息cout << endl;for(i = 0; i < v; ++i){cout << vertex[i];for(j = 0; j < v; ++j){if(ew[i][j] == MaxValue)cout << "\t∞";elsecout << "\t" << ew[i][j];}cout << endl;}}int findPos(char ch){int i;for(i = 0; i < v && ch != vertex[i]; ++i);//找到ch的位置ireturn i;}void bfs(char s)//从字符s开始广度遍历{int i, k;for(i = 0; i < v; ++i)visited[i] = 0;//访问标志置0i = findPos(s);if(i >= v)return;visited[i] = 1;queue<char> q;q.push(s);cout << "从 " << s << " 开始广度优先遍历结果：" << endl;while(!q.empty()){char w = q.front();cout << w << " ";q.pop();k = findPos(w);for(i = 0; i < v; ++i){if(ew[k][i] != MaxValue && !visited[i]){visited[i] = 1;q.push(vertex[i]);}}}cout << endl;}void bfs(char s, char t)//从字符s开始广度优先搜索t{if(s == t)return;int i, k;k = findPos(s);if(k >= v)return;//s不存在for(i = 0; i < v; ++i)visited[i] = 0;//访问标志置0visited[k] = 1;//访问s，存入队列queue<char> q;q.push(s);char *prev = new char [v];//记录搜索的路径for(i = 0; i < v; ++i)prev[i] = '*';cout << "从 " << s << " 开始广度优先搜索 " << t << " 路径：" << endl;while(!q.empty()){char w = q.front();q.pop();k = findPos(w);for(i = 0; i < v; ++i){if(ew[k][i] != MaxValue && !visited[i]){prev[i] = vertex[k];    //从k处找到了i位置，记录下来if(vertex[i] == t){printPath(prev, s, t, i);//递归打印路径cout << t << endl;delete [] prev;return;}visited[i] = 1;q.push(vertex[i]);}}}delete [] prev;cout << endl;}void printPath(char *prev, char s, char t, int i){int k = findPos(prev[i]);if(prev[k] != '*' && t != s){printPath(prev, s, prev[k], k);//递归打印路径}cout << prev[i] << " ";}
};int main()
{arrGraph ag(8,10);    //8个顶点，10条边，默认生成无向图ag.creatGraph();
//    A — B — C
//    |   |   |
//    D — E — F
//        |   |
//        G — H
//请输入A B C D E F G H  A B 1 B C 1 A D 1 B E 1 C F 1 D E 1 E F 1 E G 1 F H 1 G H 1cout << "打印图的邻接矩阵：" << endl;ag.printArrOfGraph();ag.bfs('B');ag.bfs('A','G');
}

在这里插入图片描述

3.6 DFS代码（基于邻接矩阵）

void dfs_r(char s)//从字符s开始递归深度优先遍历
{int i, j;i = findPos(s);if(i >= v)return;j = i;//j存储了开始字符s的位置for(i = 0; i < v; ++i)visited[i] = 0;//访问标志置0cout << "从 " << s << " 开始深度优先遍历结果（递归）：" << endl;for(i = 0; i < v; ++i,++j){if(j == v)j = 0;if(!visited[j])//没有访问dfs_recu(j);}cout << endl;
}
void dfs_recu(int k)
{visited[k] = 1;cout << vertex[k] << " ";for(int i = 0; i < v; ++i){if(ew[k][i] != MaxValue && !visited[i])dfs_recu(i);}
}void dfs_r(char s, char t)//从字符 s 开始递归深度优先搜索 t
{cout << "从 " << s << " 开始深度优先搜索 " << t << " 路径（递归）：" << endl;bool found = false;int i, j;char *prev = new char [v];//记录搜索的路径for(i = 0; i < v; ++i)prev[i] = '*';i = findPos(s);j = i;//j存储了开始字符s的位置if(i >= v)return;if(s == t)return;for(i = 0; i < v; ++i)visited[i] = 0;//访问标志置0for(i = 0; i < v; ++i,++j){if(j == v)j = 0;if(!visited[j])//没有访问dfs_recu(j, prev, found, s, t);}i = findPos(t);printPath(prev, s, t, i);//递归打印路径cout << t << endl;delete [] prev;
}
void dfs_recu(int k, char *prev, bool &found, char s, char t)
{if(found == true)//如果已经找到了，for循环剩余的不执行（优化）return;visited[k] = 1;if(s == t){found = true;return;}for(int i = 0; i < v; ++i){if(ew[k][i] != MaxValue && !visited[i]){prev[i] = vertex[k];    //从k处找到了i位置，记录下来dfs_recu(i, prev, found, vertex[k], t);}}
}void dfs(char s)//从字符s开始深度优先遍历（非递归）
{int i, k;i = findPos(s);if(i >= v)return;k = i;//k存储了开始字符s的位置for(i = 0; i < v; ++i)visited[i] = 0;//访问标志置0cout << "从 " << s << " 开始深度优先遍历结果（非递归）：" << endl;stack<char> q;q.push(s);visited[k] = 1;while(!q.empty()){char w = q.top();q.pop();k = findPos(w);if(visited[k])//访问过了{cout << w << " ";for(i = 0; i < v; ++i){if(ew[k][i] != MaxValue && !visited[i]){visited[i] = 1;q.push(vertex[i]);}}}}cout << endl;
}void dfs(char s, char t)//从字符s开始深度优先搜索t（非递归）
{cout << "从 " << s << " 开始深度优先搜索 " << t << " 路径（非递归）：" << endl;if(s == t)return;int i, k;i = findPos(s);k = i;//k存储了开始字符s的位置if(i >= v)return;for(i = 0; i < v; ++i)visited[i] = 0;//访问标志置0char *prev = new char [v];//记录搜索的路径for(i = 0; i < v; ++i)prev[i] = '*';stack<char> q;q.push(s);visited[k] = 1;while(!q.empty()){char w = q.top();q.pop();k = findPos(w);if(visited[k])//访问过了{for(i = 0; i < v; ++i){if(ew[k][i] != MaxValue && !visited[i]){prev[i] = vertex[k];    //从k处找到了i位置，记录下来if(vertex[i] == t){printPath(prev, s, t, i);//递归打印路径cout << t << endl;delete [] prev;return;}visited[i] = 1;q.push(vertex[i]);}}}}delete [] prev;cout << endl;
}

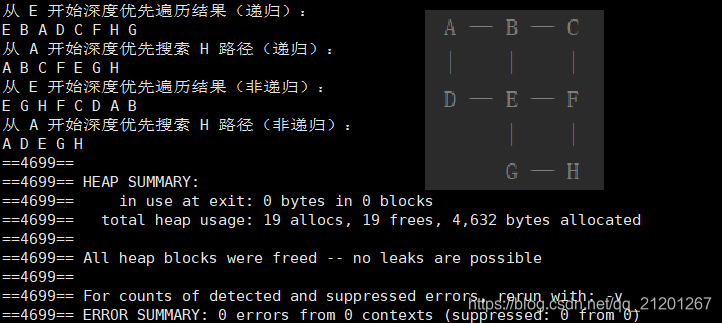
测试

	ag.dfs_r('E');ag.dfs_r('A','H');ag.dfs('E');//非递归版本dfs貌似路径不太合理,// 如 B E G H F D C A && E G H F C D A B//可能非递归版的dfs就不叫dfs了，我瞎说的ag.dfs('A','H');

在这里插入图片描述

基于邻接矩阵的 BFS&DFS 完整代码：https://github.com/hitskyer/course/blob/master/dataAlgorithm/chenmingming/graph/arrayGraph.cpp