原文地址:
<di:https://blog.csdn.net/weixin_44696674/article/details/88231922iv id=“article_content” class=“article_content clearfix” data-track-view="{“mod”:“popu_307”,“con”:",https://blog.csdn.net/weixin_44696674/article/details/88231922,"}" data-track-click="{“mod”:“popu_307”,“con”:",https://blog.csdn.net/weixin_44696674/article/details/88231922"}">
数据共41188条,选自UCI机器学习库中的「银行营销数据集(Bank Marketing Data Set)」,这些数据与葡萄牙银行机构的营销活动相关。这些营销活动以电话为基础,一般,银行的客服人员需要联系客户至少一次,以此确认客户是否将认购该银行的产品(定期存款)。
通过与葡萄牙银行机构的直销活动(电话)有关的一些数据,预测客户是否会订阅定期存款(变量Y)。这对于实际生产有着巨大作用,可以通过这个预测结果对未来的工作进行一个初步规划,同时也可以对某些用户是否会订阅定期存款提供一个参照等;
数据说明
客户信息:
Age:年龄
Job:工作,工作类型(分类:“行政管理”、“蓝领”、“企业家”、“女佣”、“管理”、 “退休”、“个体户”、“服务”、“学生”、“技术员”、“失业”、“未知”)
Marital:婚姻,婚姻状况(分类:离婚,已婚,单身,未知)(注:“离婚”指离婚或丧偶)
Education:教育(分类:‘基本.4y’,‘Basy.6y’,‘Basy.9y’’,‘Health.学校’,‘文盲’,‘专业’课程,‘大学学位’,‘未知’)
Default:违约,信用违约吗?(分类:“不”,“是”,“不知道”)
Housing:房,有住房贷款吗?(分类:“不”,“是”,“不知道”)
Loan:贷款,有个人贷款吗?((分类:“不”,“是”,“不知道”)
预测相关的其他数据:
Contact:接触方式(分类:“移动电话”,“固定电话”)
Month:月,最后一个联系月份(分类:‘MAR’,…,‘NOV’,’DEC’)
Day_of_week:每周的天数,最后一周的联系日(分类):“Mon”、“Tee”、“We”、“TUU”、“FRI”
Duration:持续时间,最后的接触持续时间,以秒为单位
Campaign:在这次战役和这个客户联系的执行人数量
Pdays:客户上次从上次活动中联系过去之后的天数(数字;999表示以前没有联系过客户)
Previous:本次活动之前和本客户端的联系人数(数字)
Proutcome:前一次营销活动的结果(分类:失败,不存在,成功)
社会和经济背景属性
EMP.var.rate:就业变化率-季度指标(数字)
cons.price.idx:消费者价格指数-月度指标(数字)
cons.conf.idx:消费者信心指数-月度指标(数字)
euribor3m::欧元同业拆借利率3个月利率-每日指标(数字)
nr.employed:员工人数-季度指标(数字)
输出变量:
Y -客户是否会定期存款?“是”、“否”
数据预处理
- 删除用户ID
- 缺失值处理,观察数据可以得知,数值型变量没有缺失,非数值型变量可能存在unknown值。
(1)删除 “unknown”
(2)缺失值分析
(3)采用随机森林对缺失值进行插补
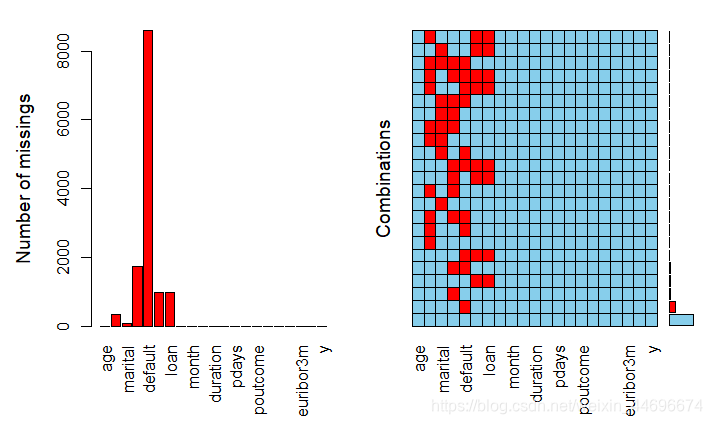
可以看到部分数据中缺失值的情况还是比较严重的,直接删除会对预测结果有较大影响,采取效果较好的随机森林插补缺失值的方法。在数据量较大的情况下,插补时间较长。
#随机森林插补缺失值
> library(missForest)
> data=missForest(mydata)missForest iteration 1 in progress...done!missForest iteration 2 in progress...done!missForest iteration 3 in progress...done!missForest iteration 4 in progress...done!
> intact=data$ximp
> md.pattern(intact)job marital education default housing loan contact month day_of_week duration campaign
[1,] 1 1 1 1 1 1 1 1 1 1 1
[2,] 0 0 0 0 0 0 0 0 0 0 0pdays previous poutcome emp.var.rate cons.price.idx cons.conf.idx euribor3m nr.employed y
[1,] 1 1 1 1 1 1 1 1 1 0
[2,] 0 0 0 0 0 0 0 0 0 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
描述性分析
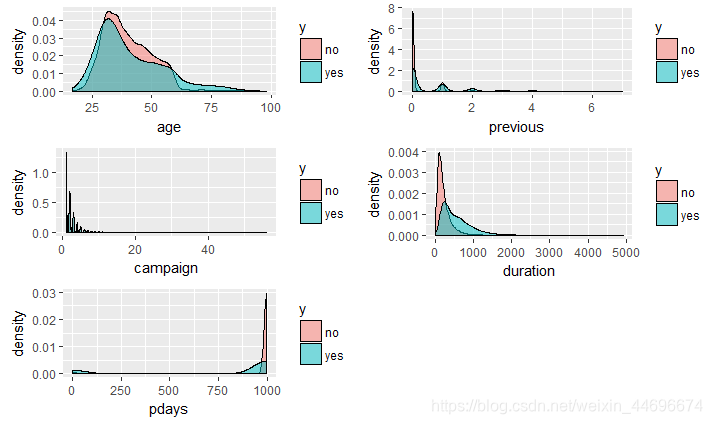
连续性变量
年轻的客户更愿意购买银行的定期存款,
接触时间过长的客户反而不会购买,之前联络人数较多的也不会购买。
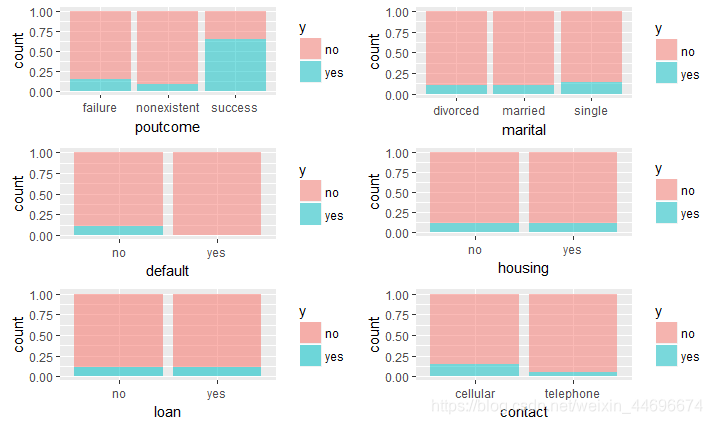
 可以看到相对于有贷款的客户,没有贷款的客户更愿意参加活动,可能是由于有贷款的客户自身没有能力去消费这样一种定期存款的产品。
可以看到相对于有贷款的客户,没有贷款的客户更愿意参加活动,可能是由于有贷款的客户自身没有能力去消费这样一种定期存款的产品。
老顾客继续购买的概率高很多,与其他理财产品相比,定期存款风险小,购买者多数不愿意承担其他理财产品高风险带来的高收益率,所以老顾客中风险偏好者更少,购买率会比较高。
单身者购买率较高,可能由于单身者在财务方面更为自由一些。
采用移动电话进行联系的效果更好,可能是由于移动电话更容易联系到客户。
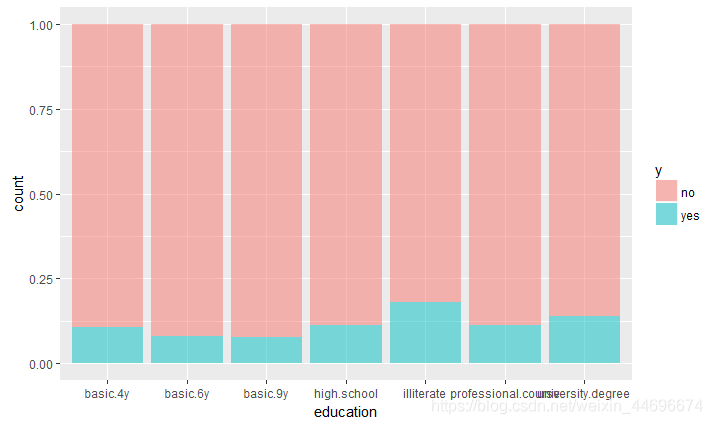
在不同学历中,不识字者的购买率最高,其次是大学本科学历,可能由于不识字者对于其他投资方式了解较少
在不同的职业中,购买率最高依次为 学生,退休者以及行政管理
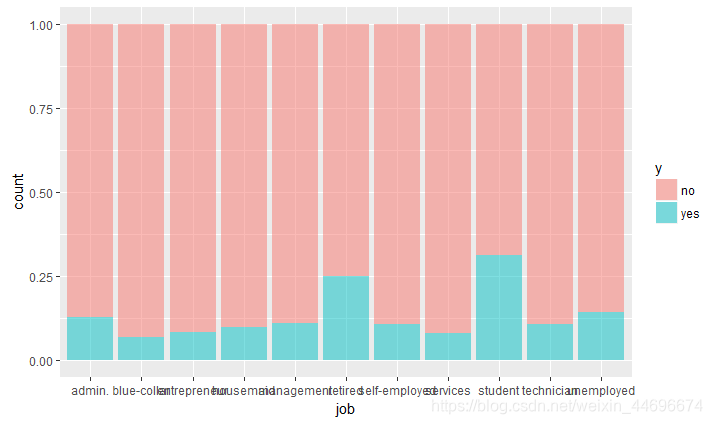
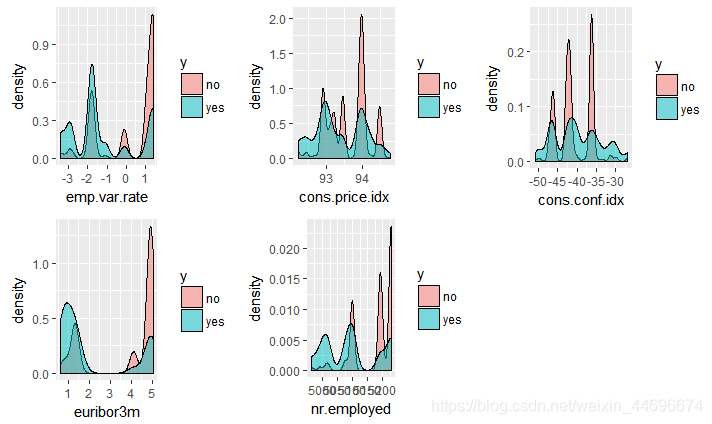
社会环境
处理数据不平衡
首先,检查正负的不平衡度,数据集中只有11%的正样本,其余89%都属于负类数据的不平衡性较为严重。
> prop.table(table(intact$y))no yes
0.8873458 0.1126542
- 1
- 2
- 3
- 4
在分类模型中,数据不平衡问题会使得学习模型倾向于把样本分为多数类,但我们常常更关心少数类的预测情况。
为减弱数据不均衡问题带来的不利影响,在数据层面有两种较简单的方法:过抽样和欠抽样。
欠采样,通过随机从样本较多的数据类中采样得到一个较小的子集,将此子集和数据较少的类结合作为新的数据集。优点是在平衡数据的同时减小了数据量,加速训练,尤其是当样本集规模很大的时候。但是这也正是造成其缺点的主要原因,数据减少会影响模型的特征学习能力和泛化能力。
过抽样方法通过增加少数类样本来提高少数类的分类性能 ,最简单的办法是简单复制少数类样本。优点是相对于欠抽样的方法,过抽样没有导致数据信息损失,在实际操作中一般效果也好于欠抽样。但是由于对较少类别的复制,过抽样增加了过拟合的可能性。
这里使用人工数据合成法来对原始数据的正样本进行更好的估计。人工数据合成法(Synthetic Data Generation)也是一种过采样技术,是利用人工数据而不是重复原始观测来解决不平衡性。ROSE(Random Over Sampling Examples)包可以帮助我们基于采样和平滑自助法(smoothed bootstrap)来生成人工样本。
library(ROSE)
data.rose=ROSE(y~ ., data =intact, seed = 1)$data
table(data.rose$y)
str(data.rose)
> table(data.rose$y)
no yes
20633 20555
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
抽取训练集测试集,采用分层抽样,抽取70%的训练集和30%的测试集。
模型及评价
在这次案例分析中,分别采用了支持向量机与随机森林进行分类,并且通过混淆矩阵来对模型进行评价,可以看到两个模型的预测效果都非常好,但是随机森林更胜一筹。
总体来说,已经达到令人相当满意的准确率了。
| 模型 | 训练集准确率 | 测试集准确率 | Kappa系数 |
|---|---|---|---|
| 支持向量机 | 0.9731411 | 0.9691882 | 0.9692 |
| 随机森林 | 1 | 0.9749161 | 0.9479 |
## 支持向量机 s_mod=svm(y~ .,train) s_predict=predict(s_mod,test) s_train=predict(s_mod,train) > sum(diag(table(train$y,s_train)))/length(s_train) [1] 0.9731411 > sum(diag(table(test$y,s_predict)))/length(s_predict) [1] 0.9691882 > confusionMatrix(data=s_predict,reference=test$y) Confusion Matrix and StatisticsReference
Prediction 0 1
0 2476 5
1 151 2431
Accuracy : 0.9692 95% CI : (0.9641, 0.9738)
No Information Rate : 0.5189
P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.9384
Mcnemar’s Test P-Value : < 2.2e-16
Sensitivity : 0.9425 Specificity : 0.9979 Pos Pred Value : 0.9980 Neg Pred Value : 0.9415 Prevalence : 0.5189 Detection Rate : 0.4890
Detection Prevalence : 0.4900
Balanced Accuracy : 0.9702
'Positive' Class : 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
## 随机森林分类 u_tree=randomForest(y~.,data=train,importance=TRUE,ntree=1000) tt_predict=predict(u_tree,test) tt_train=predict(u_tree,train) > sum(diag(table(train$y,tt_train)))/length(tt_train) [1] 1 > sum(diag(table(test$y,tt_predict)))/length(tt_predict) [1] 0.9749161 > confusionMatrix(data=t_predict,reference=test$y) Confusion Matrix and StatisticsReference
Prediction 0 1
0 2517 22
1 110 2414
Accuracy : 0.9739 95% CI : (0.9692, 0.9781)
No Information Rate : 0.5189
P-Value [Acc > NIR] : < 2.2e-16 Kappa : 0.9479
Mcnemar’s Test P-Value : 3.665e-14
Sensitivity : 0.9581 Specificity : 0.9910 Pos Pred Value : 0.9913 Neg Pred Value : 0.9564 Prevalence : 0.5189 Detection Rate : 0.4971
Detection Prevalence : 0.5015
Balanced Accuracy : 0.9745
'Positive' Class : 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
小结
可以从自变量的重要性程度了解到,社会环境整体对于销售的影响还是比较大的。
销售人员与客户接触相关因素也影响非常大,为了有一个好的销售效果,接触持续时间应该达到200h以上;同时,和客户的联系要选择固定的执行人,频繁更换人选客户购买率会下降。
其次就是老顾客率非常高,银行可以把更多精力放在老顾客的身上;而对于新客户,则可以着重关注年长退休人士。
> importance(u_tree)no yes MeanDecreaseAccuracy MeanDecreaseGini
age 53.711350 8.978287 53.725930 373.24257
job 47.306396 35.411977 55.629825 368.86332
marital 9.291924 14.580736 17.553094 65.00866
education 22.979616 34.214832 40.700215 195.76237
default 0.000000 0.000000 0.000000 0.00000
housing 2.034791 8.999713 8.003469 35.02138
loan 3.963241 10.168745 10.259191 27.48620
contact 17.776201 30.642910 21.255039 106.75061
month 115.115649 9.044732 119.975682 818.66878
day_of_week 17.576547 27.451160 31.162160 194.83529
duration 379.240942 256.048129 389.136231 3784.04379
campaign 4.377285 64.684120 56.223016 386.30141
pdays 270.409581 125.766426 268.350699 3963.38617
previous 70.901029 40.610378 78.494658 1311.44458
poutcome 30.703517 -12.585281 29.563154 246.26971
emp.var.rate 56.851807 4.849061 59.580893 864.87450
cons.price.idx 81.356412 -38.014952 77.520281 478.51227
cons.conf.idx 102.206176 -37.005703 99.402561 655.01121
euribor3m 62.765737 24.612920 66.908571 1281.83690
nr.employed 79.374570 2.185290 84.120966 1314.70020
>
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
本次案例实战,整体效果较好,准确率也比较理想,同时机器学习的大部分流程也都用到了,但是相对来说,还是有一定的缺点,例如,没有对日期数据做更多处理,由于缺少年份数据,难以对日期进行进一步分析,这点可能会对结果产生负面影响。
完整代码
file.choose()
#读取文件位置
#此处需要注意,本数据的分割方法是通过“;”
install.packages("readr")
library(readr)
mydata=read.csv("F:\\新建文件夹 (6)\\新建文件夹\\bank-additional\\bank-additional-full.csv", head=T,sep=";",stringsAsFactors = T)
str(mydata)
head(mydata)
summary(mydata)
mydata[mydata=="unknown"] = NA
library("mice")
md.pattern(mydata)
str(mydata)
head(mydata)
summary(mydata)
mydata=mydata[,-1]
##图形缺失值探索
library(VIM)
aggr(mydata,prop=FALSE,number=TRUE)
#随机森林插补缺失值
library(missForest)
data=missForest(mydata)
intact=data$ximp
md.pattern(intact)
summary(intact)
#描述性分析
library(ggplot2)
library(gridExtra)
#连续变量
g1 =ggplot(intact, aes(x=age ,fill= y ))+geom_density(alpha = 0.5)
g2= ggplot(intact, aes(x= previous,fill= y ))+geom_density(alpha = 0.5)
g3 = ggplot(intact, aes(x=campaign ,fill= y ))+geom_density(alpha = 0.5)
g4 = ggplot(intact, aes(x= duration ,fill= y ))+geom_density(alpha = 0.5)
g5 = ggplot(intact, aes(x= pdays,fill= y ))+geom_density(alpha = 0.5)
grid.arrange(g1,g2,g3,g4,g5, ncol = 2, nrow = 3)
#离散变量
g6 = ggplot(intact, aes(x= poutcome,fill= y ))+geom_bar(alpha = 0.5,position = “fill”)
g7 = ggplot(intact, aes(x=marital,fill= y ))+geom_bar(alpha = 0.5,position = “fill”)
g8 = ggplot(intact, aes(x=education,fill= y ))+geom_bar(alpha = 0.5,position = “fill”)
g9 =ggplot(intact, aes(x=default,fill= y ))+geom_bar(alpha = 0.5,position = “fill”)
g10 = ggplot(intact, aes(x= housing,fill= y ))+geom_bar(alpha = 0.5,position = “fill”)
g11= ggplot(intact, aes(x=loan,fill= y ))+geom_bar(alpha = 0.55,position = “fill”)
g12 = ggplot(intact, aes(x= contact,fill= y ))+geom_bar(alpha = 0.5,position = “fill”)
g13 =ggplot(intact, aes(x=job ,fill= y ))+geom_bar(alpha = 0.5,position = “fill”)
grid.arrange(g6,g7,g8,g9,g10,g11,g12,g13,ncol = 3, nrow = 3)
##处理非平衡分类
table(intacty)prop.table(table(intacty) prop.table(table(intacty)prop.table(table(intacty))
#欠采样会损失信息,过采样容易导致过拟合
library(ROSE)
data.rose=ROSE(y~ ., data =intact, seed = 1)datatable(data.rosedata table(data.rosedatatable(data.rosey)
str(data.rose)
#载入分层抽样的包
library(sampling)
n=round(0.8*nrow(data.rose)/2)
sub_train=strata(data.rose,stratanames=(“y”),size=rep(n,2),method=“srswor”)
train=data.rose[sub_trainIDunit,]test=data.rose[−subtrainID_unit,] test=data.rose[-sub_trainIDunit,]test=data.rose[−subtrainID_unit,]
str(train)
str(test)
library(“caret”)
library(“e1071”)
##支持向量机(SVM)分类
set.seed(0)
s_mod=svm(y~ .,train)
s_predict=predict(s_mod,test)
#分类效果
s_train=predict(s_mod,train)
sum(diag(table(trainy,strain)))/length(strain)sum(diag(table(testy,s_train)))/length(s_train) sum(diag(table(testy,strain)))/length(strain)sum(diag(table(testy,s_predict)))/length(s_predict)
confusionMatrix(data=s_predict,reference=test$y)
###随机森林
set.seed(123)
library(“randomForest”)
users_tree=randomForest(y~.,data=train,importance=TRUE,ntree=100)
t_predict=predict(users_tree,test)
t_train=predict(users_tree,train)
sum(diag(table(trainy,ttrain)))/length(ttrain)sum(diag(table(testy,t_train)))/length(t_train) sum(diag(table(testy,ttrain)))/length(ttrain)sum(diag(table(testy,t_predict)))/length(t_predict)
confusionMatrix(data=t_predict,reference=testKaTeX parse error: Expected 'EOF', got '#' at position 4: y) #̲改变数目 u_tree=ran…y,tt_train)))/length(tt_train)
sum(diag(table(testy,ttpredict)))/length(ttpredict)confusionMatrix(data=tpredict,reference=testy,tt_predict)))/length(tt_predict) confusionMatrix(data=t_predict,reference=testy,ttpredict)))/length(ttpredict)confusionMatrix(data=tpredict,reference=testy)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
</div><link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-e44c3c0e64.css" rel="stylesheet"></div>










)



:事务+List集合+慢查询SQL+Redis+秒杀设计)
)
)


落地的思考)