说明

关于CNN的基础知识：卷积、填充、步长、池化、完整的深度CNN网络可以参考
链接: AI学习笔记——卷积神经网络（CNN）.
本文主要侧重介绍这些操作背后的具体含义并且记录一下吴恩达老师课程的知识点。

卷积 Convolution

卷积层主要就是通过filter来过滤图片中的边缘（线条），如下图为“垂直边缘检测”的例子，矩阵中数字1代表亮度，0代表灰度，-1代表黑度。第一个输入矩阵代表的图案如下面的小图片所示，图片中间会产生一个由亮到暗的竖直线条，使用从亮到暗的垂直边缘过滤器进行过滤后，结果可以表示原图片中间有一个竖直线条（且该线条是由亮处到暗处的线条），第二个输入矩阵经相同过滤器过滤后，结果可以表示原图片中间有一个竖直线条（且该线条是由暗处到亮处的线条）：

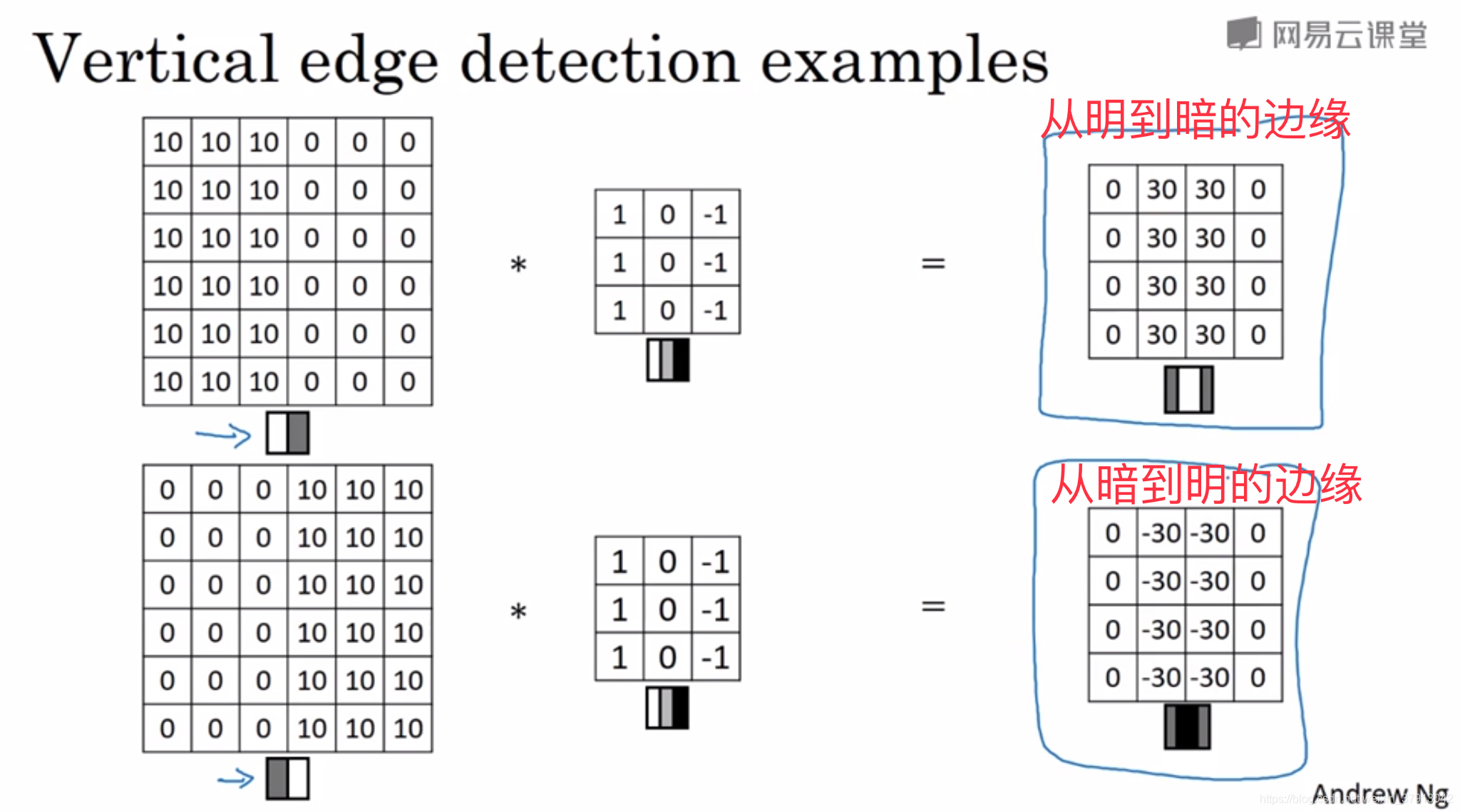
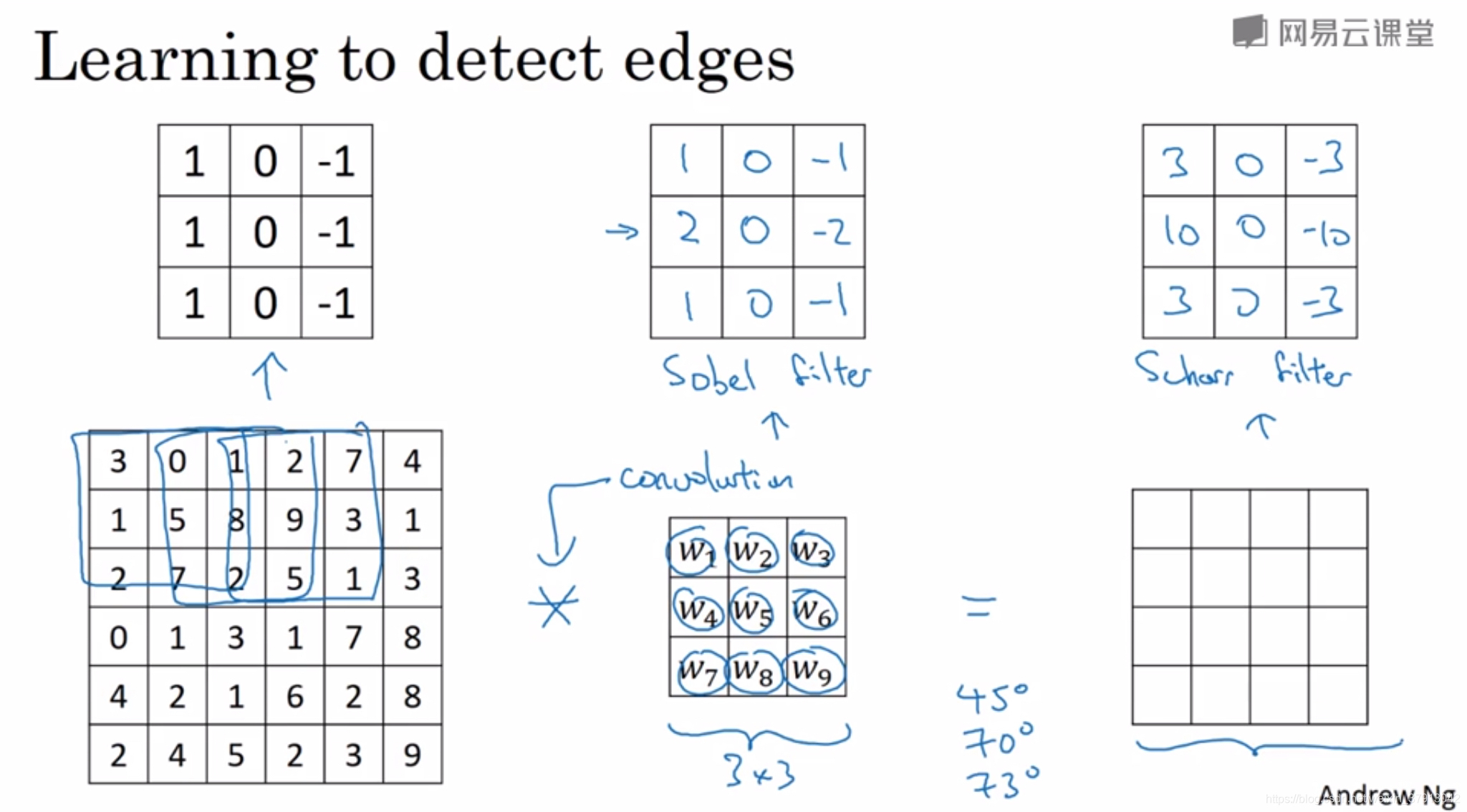
当然会有不同类型的过滤器：水平过滤器、垂直过滤器、sobel filter、schar filter ···
使用不同的过滤器可以过滤图片中不同类型的边缘（线条）
同时，由于过滤器本身是参数，在反向传播过程中，网络可以自己学习参数，使过滤器更好的过滤图片。

填充 Padding

填充指在原图片矩阵的周围填充元素0
解决的问题：1、卷积之后图片尺寸变小 2、原图片边缘信息的丢失

根据是否进行填充，将卷积分为：
Valid convolutions：不进行填充，卷积后图片尺寸变为（n-f+1）*（n-f+1）
Same convolution：填充p=（f-1）/2，卷积后图片尺寸和原来一样

步长 Stride

当过滤器不能按照指定步长将图片完整过滤时，最后一个步长变小，以完成图片过滤。
所以最终图片的尺寸公式将如下所示：
过滤器f一般等于奇数，不用偶数原因：
1、不对称填充（左边填充两列，右边填充一列）
2、奇数过滤器会有一个中心点，在计算机视觉里，如果有一个中心像素会更方便，便于指出过滤器的位置

RGB图像卷积

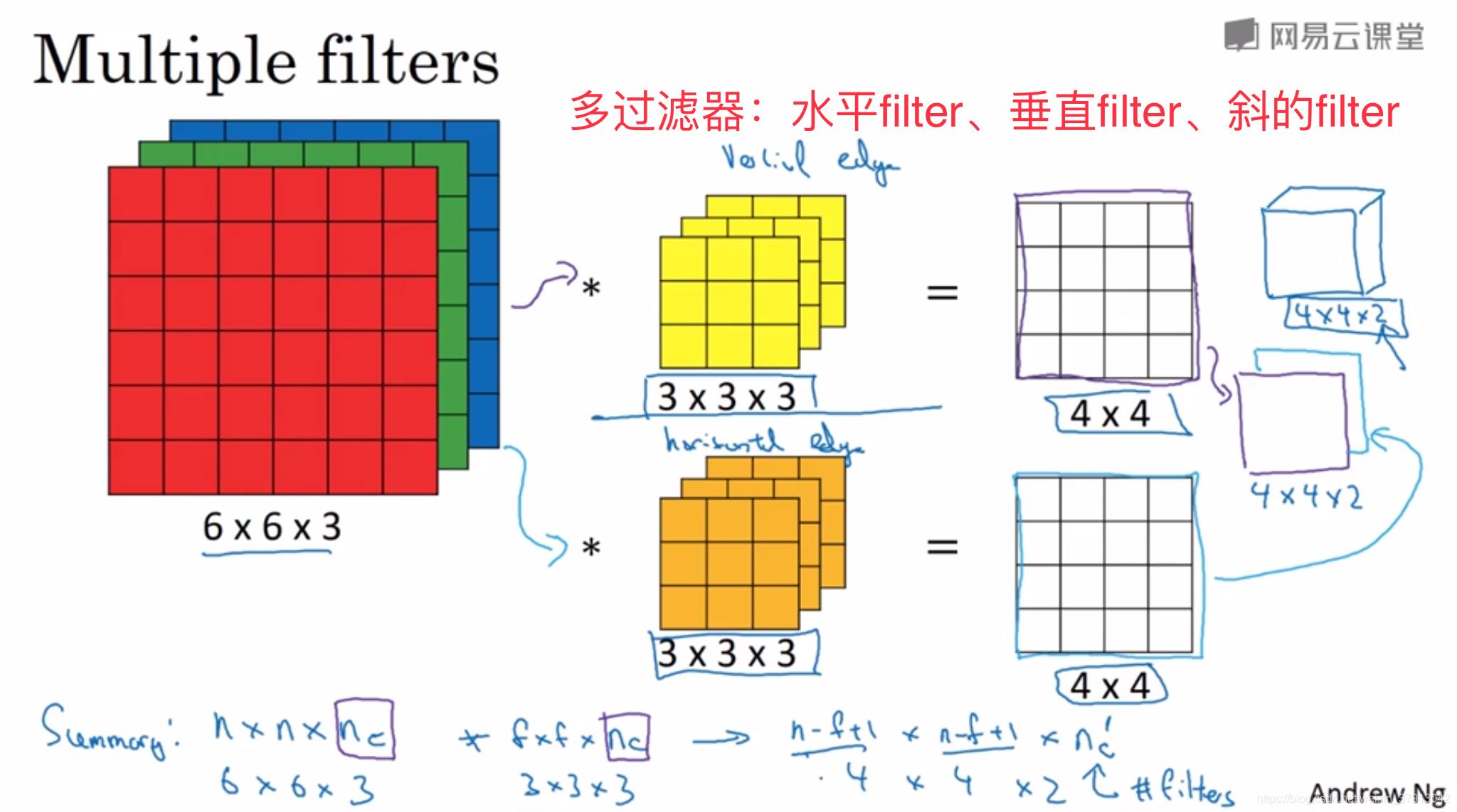
过滤器的通道（channel）要与其所过滤的图片通道在数量上保持一致，每个通道的过滤器可以是不同类型的，并且可以有多个过滤器进行过滤，最后将结果整合到一起

池化 Pooling

功能：缩减模型、提高计算速度、提高所提取特征的鲁棒性（robust）
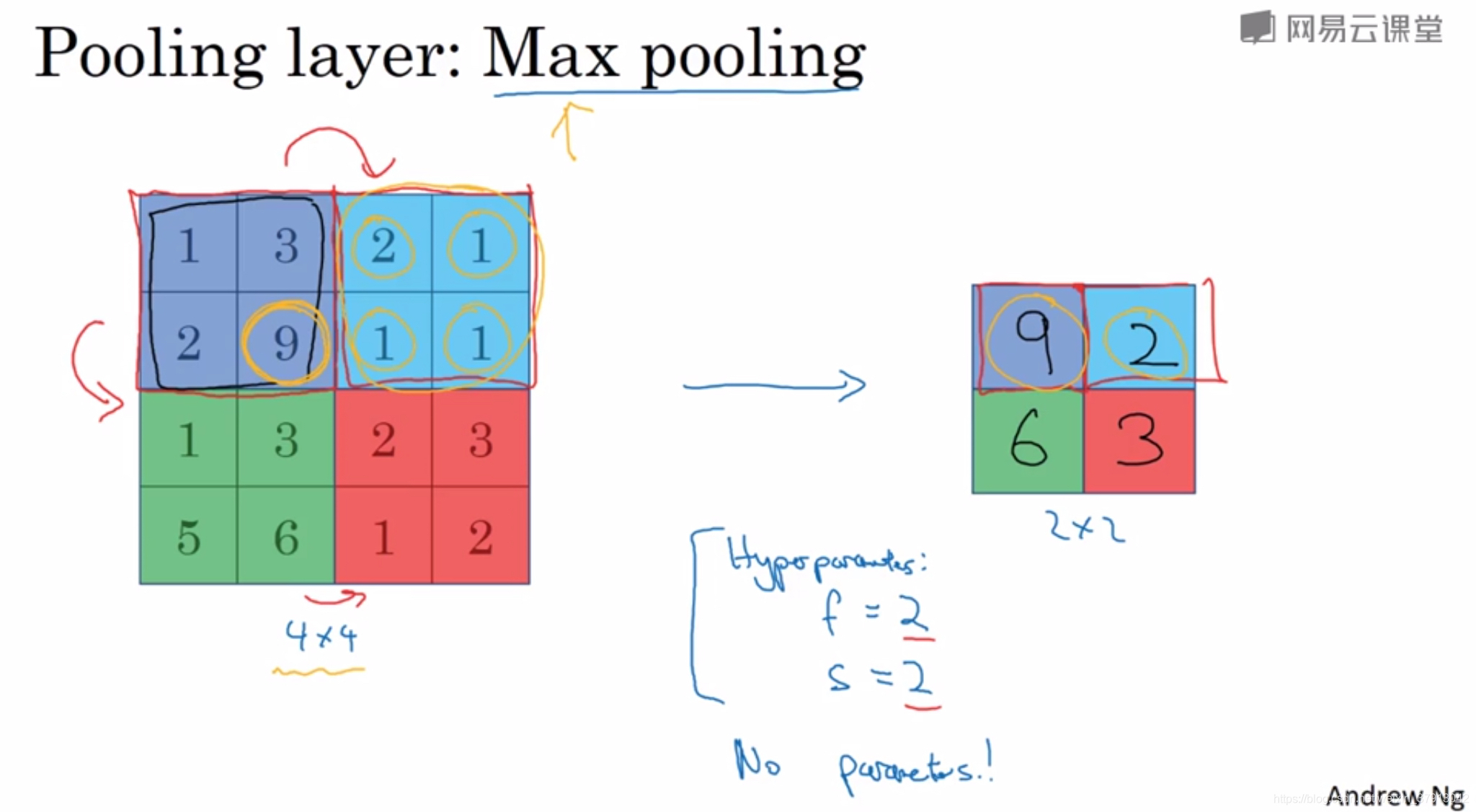
有Max-Pooling和Average-Pooling两种池化方式，一般常用的是最大池化。
第一个图片中紫色、蓝色、绿色和红色4*4的矩阵都可以看作是某些特征的集合，大的数字意味着可能提取了某些特定特征。最大化操作的的功能就是只要在任何一个象限内提取到某个特征，他都会保留在最大池化的输出里面（如紫色象限的9），如果没有提取到某个特征，那么其中的最大值也还是很小（如蓝色象限的2）。

完整CNN

一般完整的CNN网络由 卷积-池化-全连接 组成

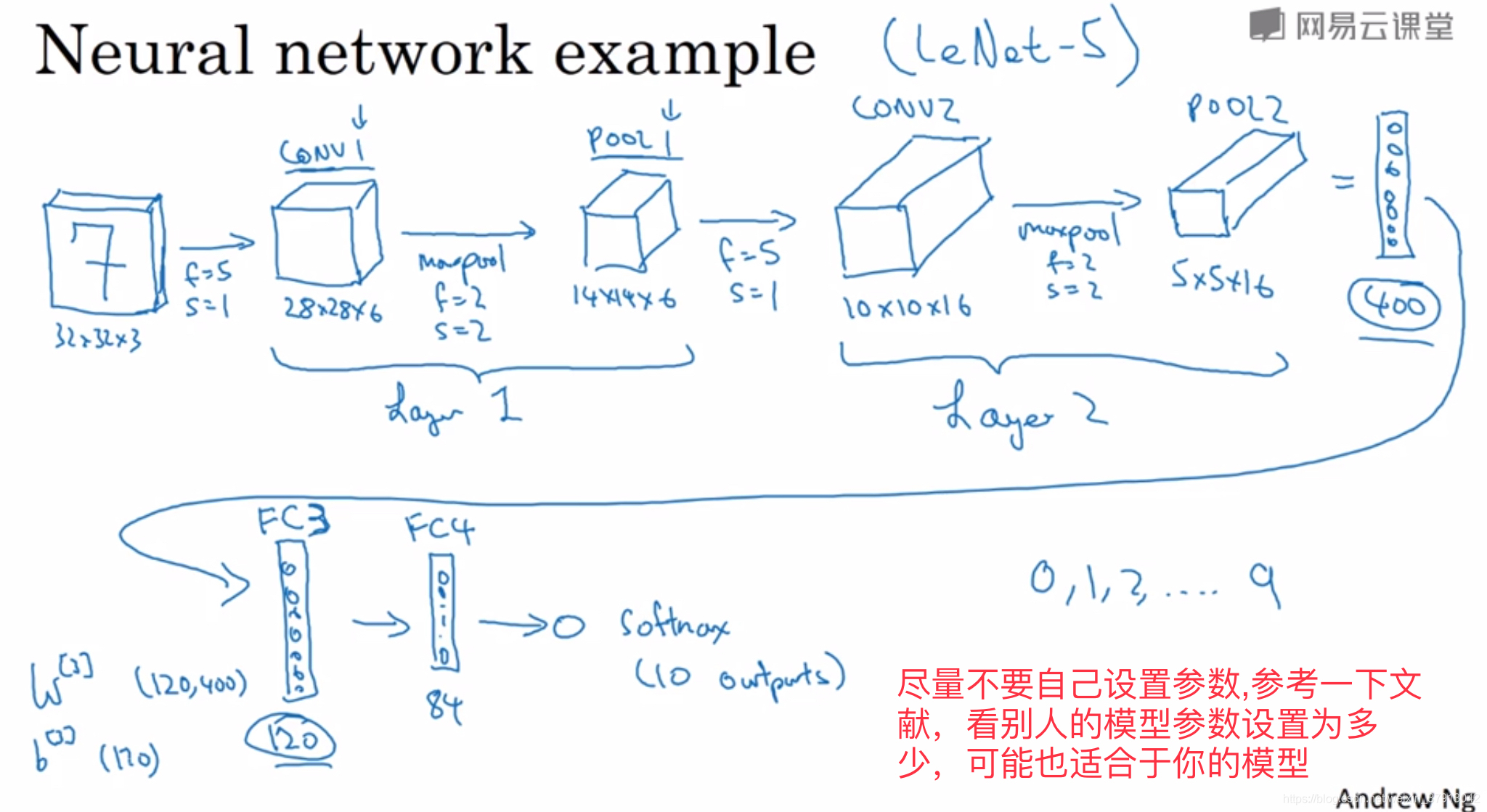
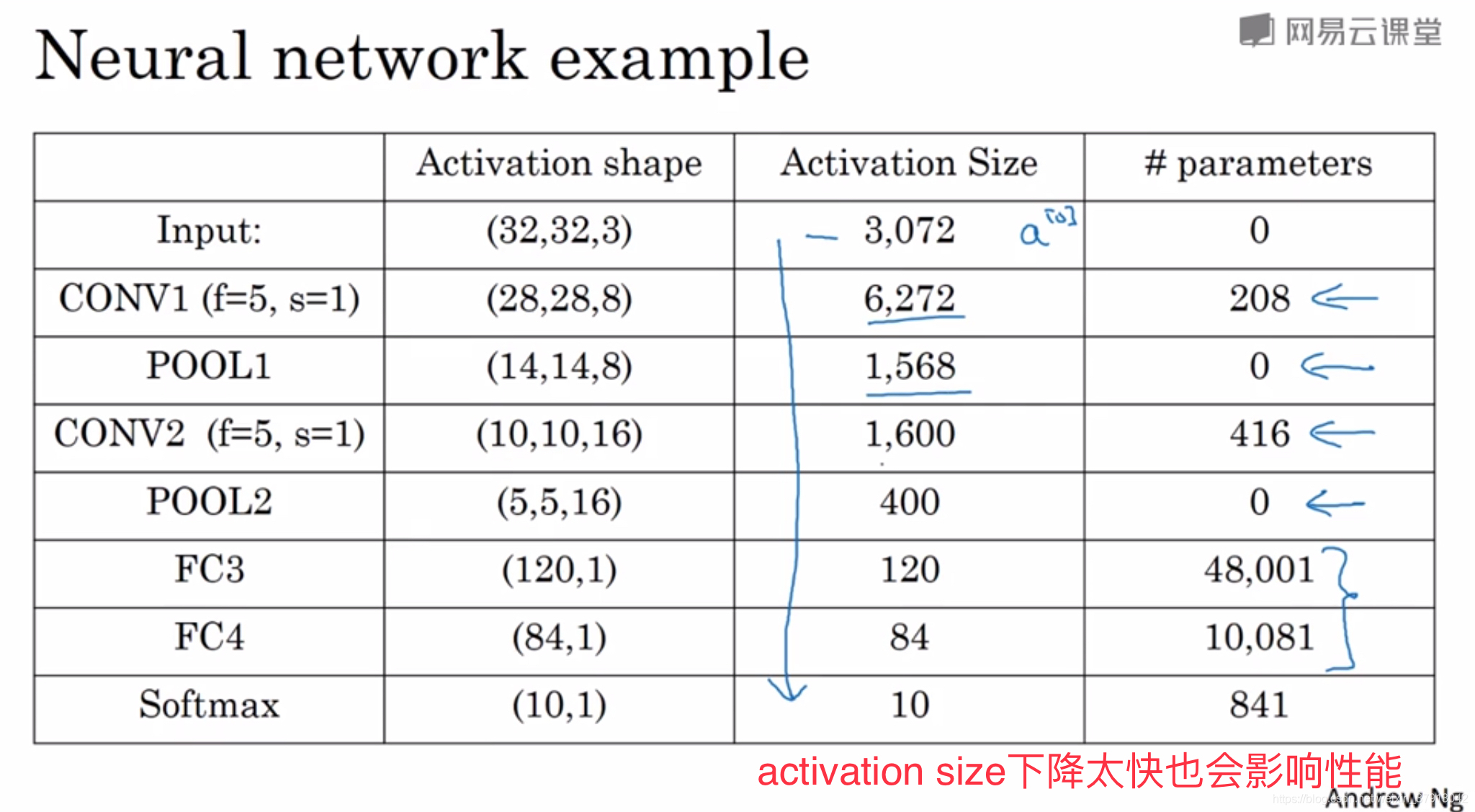
为什么人们喜欢用卷积神经网络？

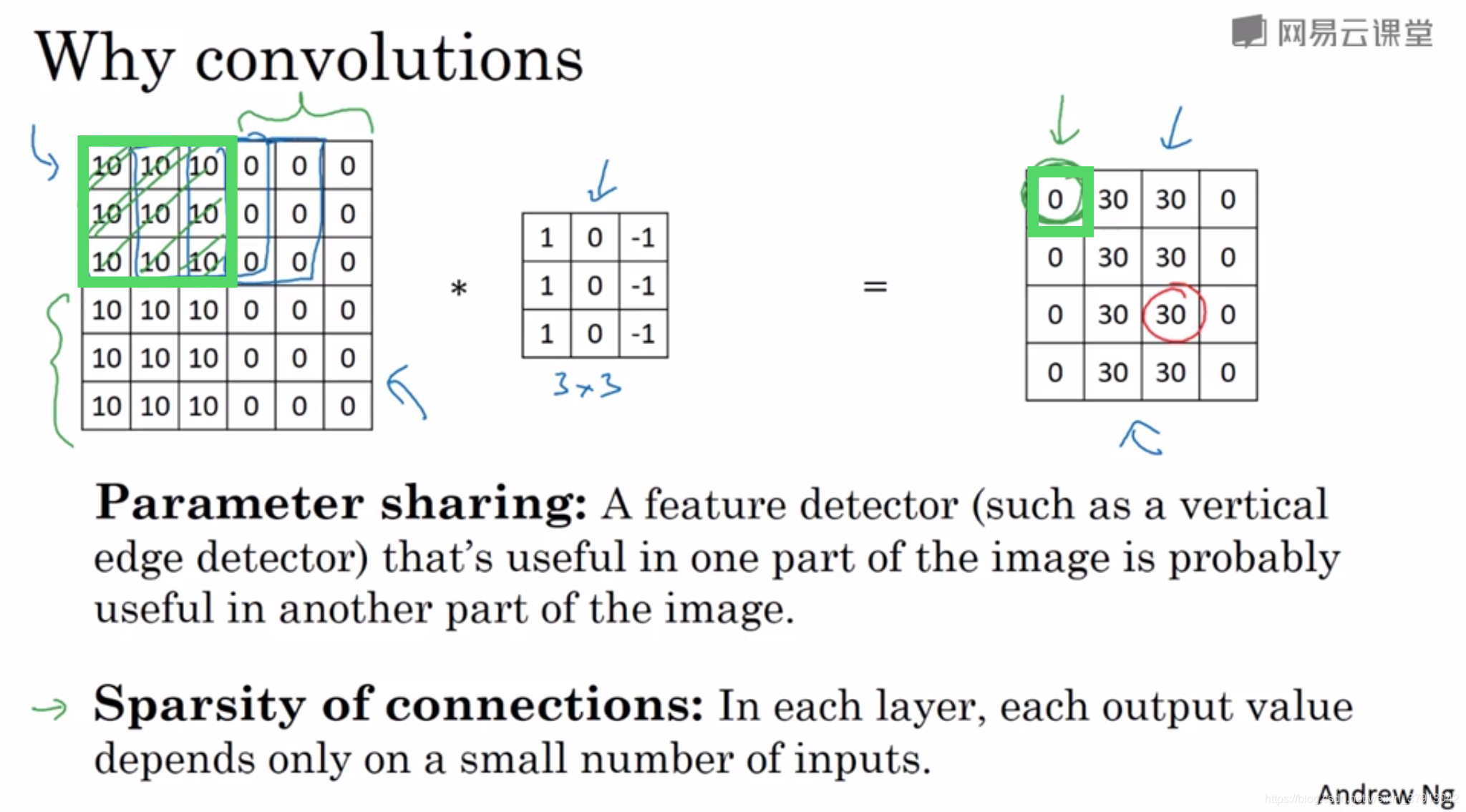
参数共享：可以在输入图片的不同区域使用同样的参数（同一个过滤器进行全图扫描）
稀疏连接：举例，输出左上角的0，是通过3 * 3的卷积计算得到的，他只依赖于输入矩阵左上角3*3的单元格。（即一个输出与9个输入连接，对比FC，一个输出与所有的输入连接）

1、神经网络可以通过这两种机制减少参数，以便我们用更小的训练集来训练它，从而预防过拟合。
2、卷积神经网络善于捕捉平移不变，通过观察可以发现，像右移动两个像素，图片中的猫依旧清晰可见，因为神经网络的卷积结构，即使移动几个像素，这张图依然具有非常相似的特征，应该属于同样的输出标记。

实例分析

为什么进行实例分析？
因为在计算机视觉任务中表现良好的神经网络框架，往往也适用于其他任务。

LeNet-5：针对灰度图像训练的

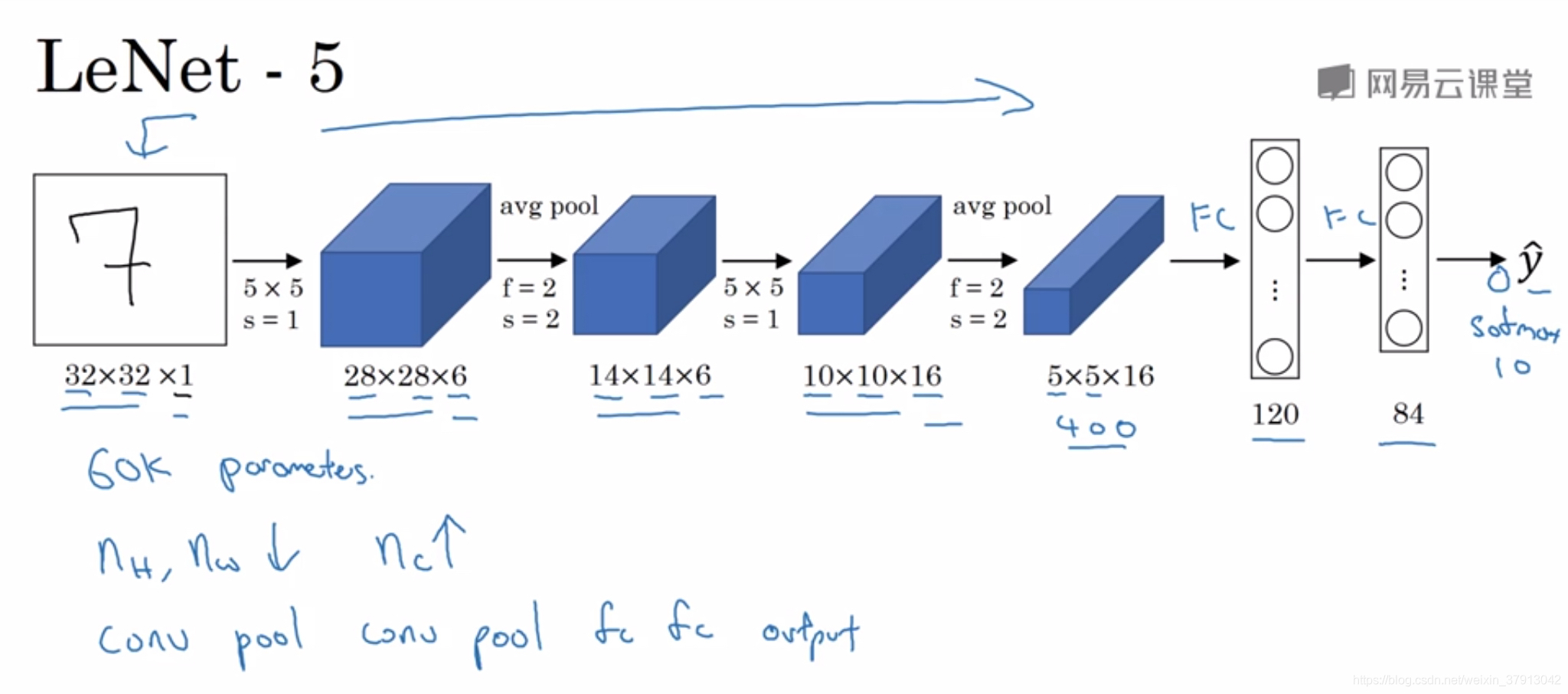
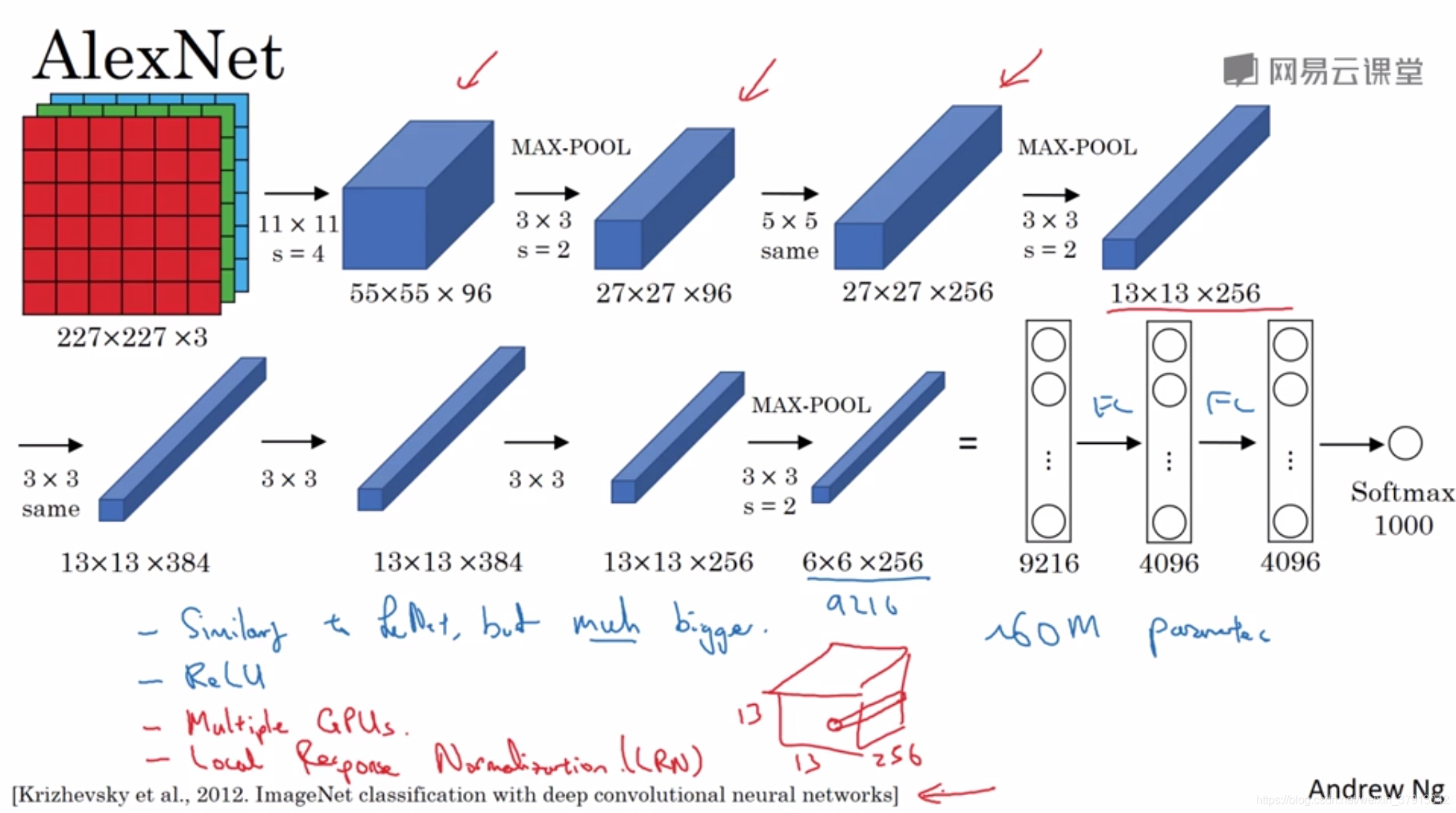
AlexNet：

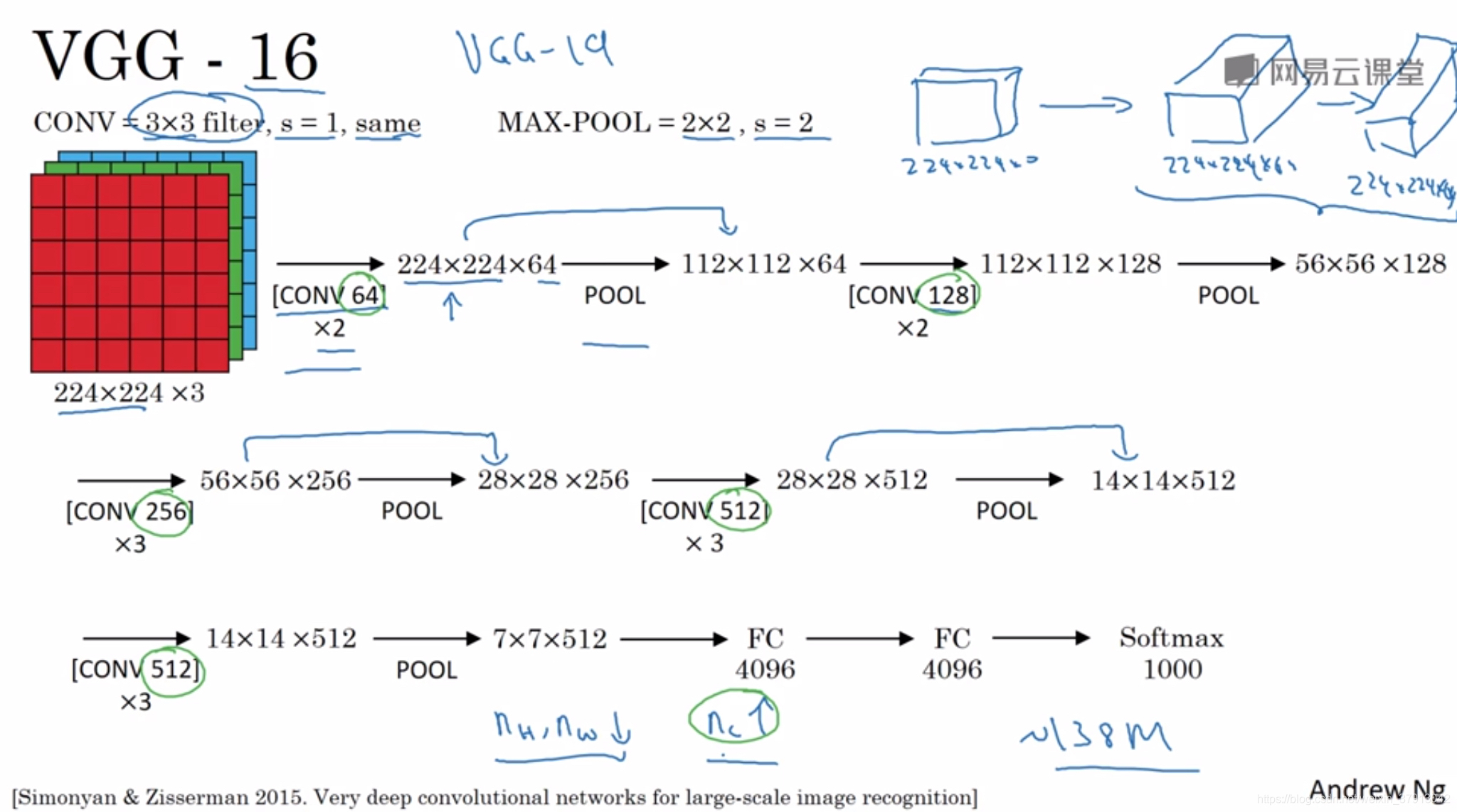
VGG-16: 16指这个网络包含了16个卷积层和全连接层，参数挺多的，但是网络结构比较规整。
文中揭示了，随着网络的加深图像的高度和宽度都以一定的规律不断缩小，每次池化后刚好缩小一半。信道的数量在不断增加，而且刚好也是在每组卷积操作后增加一倍。也就是说，图像缩小的比例和信道增加的比例是有规律的。