文章目录
- 1.概念
- 2.构造最小生成树Prim算法
- 3.构造最小生成树Kruskal算法
1.概念
- 对图运用不同的遍历方法就可能得到图的不同遍历顺序,每一种遍历顺序对应于一棵生成树
- 对于无向连通图,所有的生成树中必有一棵树的所有边的权的总和最小的,称之为最小生成树(Minimum cost spanning tree)
练习题:
LeetCode 1135. 最低成本联通所有城市(最小生成树+排序+并查集)
LeetCode 1489. 找到最小生成树里的关键边和伪关键边(并查集+kruskal最小生成树)
2.构造最小生成树Prim算法
从某点出发(该点加入集合U),找到跟它相连接的点,从中取出权值最小的,加入集合U,对这个集合U,查找与U内所有的点相连的点的权值,取权值最小的点,加入集合U,直到所有点加入到U。
struct CloseEdge //最短的边
{int startV;int endV;int minWeight; //最小的权值bool operator < (const CloseEdge &s) const{//符号重载return minWeight < s.minWeight;}
};
//----------prim最小生成树---------------
void MiniSpanTree_Prim(char ch)
{int s = findPos(ch);if(s >= v)return;cout << "从 " << ch << " 开始的Prim最小生成树:" << endl;int i, j, k, x, w, minid, sum = 0;for(i = 0; i < v; ++i)visited[i] = 0;//访问标志置0visited[s] = 1;vector<int> q;vector<int>::iterator it;q.push_back(s);for(i = 0; i < v-1; ++i){for(it = q.begin(),x = 0; it != q.end(); ++it,++x){w = MaxValue;for(j = 0; j < v; ++j){if (!visited[j] && ew[*it][j] < w){w = ew[*it][j];minid = j;//记录较小的权的序号为k}}close_edge[x].minWeight = w;close_edge[x].startV = *it;close_edge[x].endV = minid;}sort(close_edge,close_edge+x);visited[close_edge[0].endV] = 1;cout << vertex[close_edge[0].startV] << "-" << vertex[close_edge[0].endV] << " 权值 " << close_edge[0].minWeight << endl;sum += close_edge[0].minWeight;q.push_back(close_edge[0].endV);}cout << "最小生成树权重总和为:" << sum << endl;}
我这个程序比较好理解,但是复杂度n3。书上的程序写法是n2。
int main()
{
//------------以下测试Prim最小生成树------------------
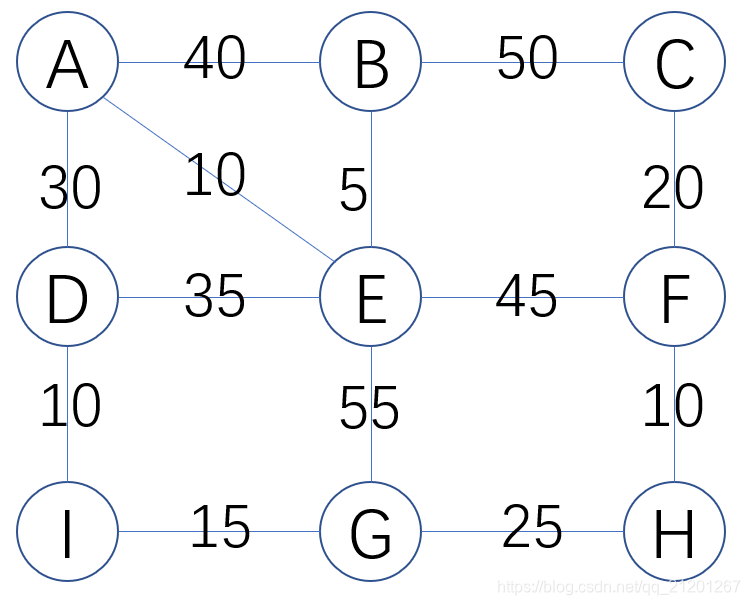
// A -40- B -50- C
// 30| \10 5| 20|
// D -35- E -45- F
// 10| 55| 10|
// I -15- G -25- H
//请输入以下数据生成上面的图
//A B C D E F G H I A B 40 B C 50 A D 30 B E 5 C F 20 D E 35 E F 45 E G 55 F H 10 G H 25 A E 10 D I 10 I G 15arrGraph bg(9,13); //9个顶点,13条边,默认生成无向图bg.creatGraph();bg.printArrOfGraph();bg.MiniSpanTree_Prim('A');bg.MiniSpanTree_Prim('I');//从任一点出发,最小花费都一样return 0;
}
完整代码:https://github.com/hitskyer/course/blob/master/dataAlgorithm/chenmingming/graph/arrayGraph.cpp

从任意一点出发最小生成树的最小代价总和都相等。
看了别人的代码,调试后,明白了n2复杂度的Prim算法
void MiniSpanTree_Prim_O_n2(char ch)
{int s = findPos(ch);if (s >= v)return;cout << "从 " << ch << " 开始的Prim最小生成树:" << endl;int i, j, k, minweight, sum = 0;int adjvex[v]; //保存顶点下标int lowcost[v]; //保存相关顶点见的权值lowcost[s] = 0; //=0,加入了生成树adjvex[s] = s; //起点下标为自己for(i = 0; i < v; ++i){if(i == s)continue;lowcost[i] = ew[s][i];//将s起点与其他点的权值初始化adjvex[i] = s;//到达i的前一个点初始化为起点}for(i = 0; i < v-1; ++i){minweight = MaxValue;for(j = 0, k = 0; j < v; ++j){if(lowcost[j] != 0 && lowcost[j] < minweight)//未加入生成树的,且j点的比较小{minweight = lowcost[j];//更新最小值k = j;//下标记录入k}}cout << vertex[adjvex[k]] << "-" << vertex[k] << " 权值 " << ew[adjvex[k]][k] << endl;lowcost[k] = 0;//最小的权值点k加入生成树sum += ew[adjvex[k]][k];for(j = 0; j < v; ++j){if(lowcost[j] != 0 && ew[k][j] < lowcost[j])//k加入生成树后,对k周围的权与最小权lowcost比较{lowcost[j] = ew[k][j];//更小的权更新lowcost数组adjvex[j] = k;//并记录j的前一位是k}}}cout << "最小生成树权重总和为:" << sum << endl;
}
3.构造最小生成树Kruskal算法
该算法思路是从边(权重)出发考虑,取最小的权出来,若该边不会造成回路就加入生成树,然后次最小,循环下去
//----------Kruskal最小生成树---------------
void MiniSpanTree_Kruskal()
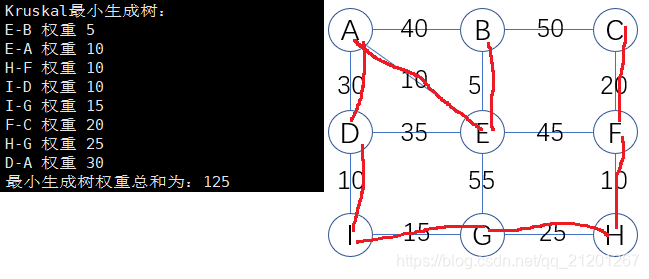
{cout << "Kruskal最小生成树:" << endl;int i, j, k = 0, sum = 0;CloseEdge edges[MaxEdgeNum]; //边数据集for(i = 0; i < v; ++i) //把边信息输入到edges数组for(j = 0; j < v; ++j)if(ew[i][j] != MaxValue && i > j)//无向图,i>j 矩阵中一半就可获取全部信息{edges[k].startV = i;edges[k].endV = j;edges[k].minWeight = ew[i][j];k++;}sort(edges,edges+k);//边排序int parent[e]; //作用,判断边与边是否形成回路int vf1, vf2;for(i = 0; i < k; ++i)parent[i] = 0;for(i = 0; i < k; ++i){vf1 = Find(parent, edges[i].startV);vf2 = Find(parent, edges[i].endV);if(vf1 != vf2)//没有回路,可以选入生成树{parent[vf2] = vf1;cout << vertex[edges[i].startV] << "-" << vertex[edges[i].endV]<< " 权重 " << edges[i].minWeight << endl;sum += edges[i].minWeight;}}cout << "最小生成树权重总和为:" << sum << endl;
}
int Find(int* parent, int v)
{int t = v;while(parent[t] > 0)t = parent[t];return t;
}






)



:事务+List集合+慢查询SQL+Redis+秒杀设计)
)
)


落地的思考)
:Redis缓存的设计、性能、应用与数据集群同步)

)
)