定义

收益和代价
对一棵生成树 T1，若将某结点的一条分枝移至另一结点作为其一条分枝后产生的生成树为 T2，考察分枝移动前后生成树的边长和的变化，则定义收益(gain)和代价(cost)分别为：

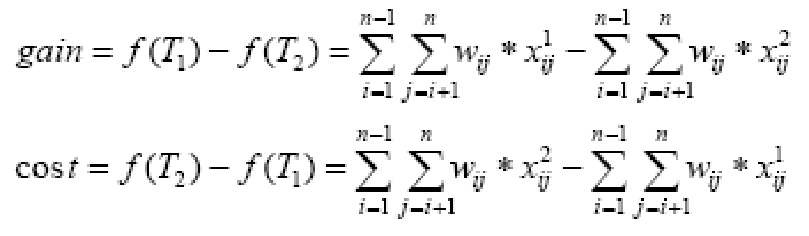
其中x¹_ij∈ T₁， x²_ij∈ T₂
从上述定义可知，收益和代价是密切相关的两个指标。对一棵生成树T1，在分枝的移动过程中，若收益大于0，则分枝移动后生成树的边长和减小，相应代价必小于0；反之亦然。

嫁接：
将生成树非考察结点且具有某种优良特性的分枝（嫁接枝）接入到非完全生成树的待考察结点中,以形成更好生成树个体(这里指收益大于0)的过程称为嫁接。

剪接：
将生成树个体考察结点的某一分枝（剪接枝）接入到非完全生成树中另一位置,以形成可行个体或更好个体的过程称为剪接 。

注意： 嫁接和剪接是两种完全不同的操作,它们发生的作用点、机理、采用的策略及对算法产生的效果完全不同。

冲突及冲突检测：
在对消除不满足约束情形进行剪接或对具有较差属性的分枝进行剪接操作的同时，若引起新的不满足约束的情形称为冲突。
在剪接过程中引起了冲突，就称找出这一冲突现象的过程为冲突检测 。

嫁接算子及策略

步骤：

1. 根据结点及其关联结点的边长信息，选择具有优良品质的嫁接枝；
2. 将选择的嫁接枝重新接入，以形成更好的生成树个体，即嫁接后收益大于0。

选取具有优良品质的嫁接枝需要解决的问题：

1. 如何利用边结点及其关联结点的边长信息
   为了使嫁接和剪接操作更为有效，对各结点按其关联结点构成边的长度进行排序，并将排序结果保存在指针变量pnodesortdis中。
2. 求任意结点的父结点及子结点关系
   采用基于度排列的编码方法。设计了通过利用度维关系查找某一结点的父结点函数FindPareNode(par1,par2)及其子结点的函数FindChildNode(par1,par2)，par1、par2为算法所需参数，它们在较好的情形下时间复杂度均为O(1)，在最坏的情形下时间复杂度为O(n)。

利用度维关系查找生成树个体某一结点的父结点算法
基本思想：从当前位置向前扫描，记录扫描过的结点的度值，根据扫描过的结点与度值的关系计算出其父结点位置。
伪码描述如下：

算法1 (检索某一结点位置nodepos的父结点位置parvpos算法). 
Input:生成树个体individual,考察结点位置nodepos. 
Output:考察结点nodepos的父结点位置parvpos. 
Begin 初始化参数:degreesum=0,counter=0,parvpos=nodepos; 根据输入的个体individual,得到其结点维individual.chrom1和度维individual.chrom2; if parvpos=1 then return 1; end if parvpos=parcpos-1,counter=counter+1; degreesum=degreesum+individual.chrom2[parvpos]; if parv>1 then degreesum=degreesum-1; end if while degreesum<counter do parvpos=parcpos-1,counter=counter+1; degreesum=degreesum+individual.chrom2[parvpos]; if parv>1 then degreesum=degreesum-1; end if end while 返回parvpos; End 

按收益优先及度约束控制嫁接策略执行嫁接操作，算法的伪码描述如下：

算法2 (嫁接算法). 
Input:生成树个体individual,完全图边长矩阵对应的二维指针变量edgelen. 
Output:经嫁接操作后新生成的个体newindividual. 
Begin 设置所有结点使用标志变量pflagnodeuse为0; 初始化参数contrpara=dc, i=1,k=1, bflaggrafting=false; while i≤ n do设置counter=0,结点i对应结点序号的标志pflagnodeuse为1; 由pnodesortdis得到与i 关联的第k个结点序号inodeassono; 由edgelen得到i 与inodeassono的边长nodedis; while counter<contrpara &&nk≤ do 求出inodeassono的父结点assoparenodeno及边长assonodedis; 计算边交换后收益gain=nodedis-assonodedis; if inodeassono不是i的子结点&& gain>0 then 选择以inodeassono代表的分枝; 设置bflaggrafting=true; end if if bflaggrafting=true then 执行嫁接操作; counter=counter+1; 设置结点inodeassono的标志pflagnodeuse为1; 设置bflaggrafting=flase; end if k=k+1; 由pnodesortdis得到与i 关联的第k个结点序号inodeassono及位置inodeassopos; 由edgelen得到i 与inodeassono的边长nodedis; end while i=i+1; end while End 

嫁接策略

1. 收益优先嫁接策略
   基本思想：对考察结点，若所选关联结点分枝移至考察结点前后收益大于0，则该分枝可选为嫁接枝。
   优点：按该策略执行嫁接，操作简便，且总体效果较好。
   缺点：嫁接后某些结点的分枝数可能大大超过给定的度约束值，从而增加剪接的负担,需要花费较长的CPU时间。

剪接算子及策略

对嫁接中产生的生成树可能包含某些结点不满足度约束，以及对经过基本遗传算子操作使其具有较差属性分枝的情形，均要进行剪接操作。

步骤：

1. 针对生成树的每一结点，考察其所有的分枝，判断当前结点具有最(较)差属性的分枝是否可作为剪接枝？
2. 若是，将该分枝插入到其关联结点上 。

判断一条分枝是否在当前位置具有最(较)差属性的依据为下列两种情形之一:

1. 若该分枝移动到另一关联结点的收益最(较)大；
2. 若所有考察的分枝分别移动收益均小于0，则指移动后代价最小的分枝。

算法3 (剪接算法). 
Input:生成树个体Individual,完全图边长矩阵对应的二维指针变量edgelen. 
Output:经剪接操作后新生成的可行个体newindividual. 
Begin 初始化剪接参数,设置iprunflag,iprunneedflag为false, 设置初始位置i=1; while  I ≤ n   do取当前结点度值nodegree; if nodegree大于给定的度约束值degreecons then 设置剪接标志iprunflag为true; end if 求解i的子结点,结果保存在指针变量pichild中; while pichild非空 do 寻找具有最差属性的子结点selectchildnode分枝 if 收益为大于0且iprunflag为false then if 检测无冲突 then 设置剪接操作标志iprunneedflag为true; else if 冲突能有效解决 设置剪接操作标志iprunneedflag为true; end if end if end if if iprunflag or iprunneedflag为true then 执行剪接操作; iprunneedflag= false; else break; end if if 剪接插入位置小于当前位置 then 指针回溯; end if 取当前位置度值nodedegree; if 当前位置度值nodegree小于等于degreecons then 设置iprunflag为flase; end if end while i=i+1; end while End

剪接策略

1. 收益优先剪接策略
   基本思想：对考察结点的所有分枝，若所选分枝移至另一结点位置后收益大于0，且未引起新不能有效解决的冲突，则该分枝可选为剪接枝，执行剪接操作。按该策略执行剪接，操作简便，且花费的CPU时间较小。
2. 双重信息剪接策略
   基本思想：对考察结点的所有分枝，在判断某一分枝是否作为剪接枝时，应将边长信息和位置次序关系信息同时进行分析。同嫁接策略类似,这是一种较为复杂的控制策略。
3. 退化剪接策略
   基本思想：当不满足度约束时，若在剪接中出现不能有效解决的冲突，只能按代价最(较)小化原则进行剪接。

GPOGA算法

在基本遗传算法体系的基础上，结合嫁接和剪接算子作用，给出基于嫁接和剪接算子的遗传算法 (A Genetic Algorithm with Grafting and Pruning Operators, 简称GPOGA) 。

算法4 (GPOGA). 
Input:与所求DCMST问题有关的数据（结点数,完全图边长等）,遗传算法基本控制参数. 
Output:生成的最好解个体及有关计算数据. 
Begin 随机初始化种群P(0),t=0; 计算P(0)中个体的适应值并按适应值排序; while 计算代数 t ≤ maxgen do j=0; while 新产生个体j<N do 根据个体的适应值随机从当代种群中选择两个父个体,设为oldindi1和oldindi2; 执行杂交操作CrossOver(oldindi1,oldindi2),将产生的新个体保存在newpop[j],newpop[j+1]中; 执行交换变异操作SwapMutation(newpop[j])、SwapMutation(newpop[j+1]);将产生的两个新 个体 复制到临时种群变量数组temp1[j]和temp1[j+1]中; 执行嫁接操作Grafting(newpop[j]), Grafting (newpop[j+1]); 执行剪接操作pruning(newpop[j]), pruning (newpop[j+1]); 计算并评价temp1[j]、temp1[j+1]、newpop[j]、newpop[j+1]、oldindi1及oldindi2的目标值,选 择两个较好的个体复制到newpop[j]及newpop[j+1]中; j=j+2; end while; 计算新种群newpop 的目标值、适应值并排序,同时以oldpop中最好的个体代替newpop中最差的个体; 将newpop种群中个体复制到oldpop中,计算其目标值、适应值并排序; t=t+1; end while; 记录及输出结果. End 

在算法中采用的选择策略称之为 (μ+λ+λ) 选择，即将随机选择的两个父个体、由基本遗传算子交换变异后产生的新个体以及经嫁接和剪接后产生的新个体共同参与竞争，以选择两个较好的个体进入下一代种群。这样做的原因是因为剪接中可能导致退化现象出现，因而将交换变异产生的两个新个体共同参与竞争，以确保算法的收敛性。

上述算法中,也可采用基于适应值概率的轮赌盘选择策略,只要将由基本遗传算子交叉变异后产生的新个体参与选择过程,或者将由基本遗传算子交叉变异后产生的最好个体与当前种群的最好个体进行比较,选择较好的个体直接进入下一代,就能确保算法以概率1收敛到全局最优解。

总结

度约束最小生成树（DCMST）问题是一类难解的NP-hard问题，目前尚未有可靠、有效的解决方法。通过对现有方法存在的问题和缺陷进行分析，借鉴花草果树的人工种植和培育技术,设计的基于嫁接和剪接算子的遗传算法(GPOGA)，理论分析和实验数据都为算法的正确性和有效性提供了依据。 GPOGA的三类算子在计算过程中互为补充,协同完成优化搜索过程，从而使算法的性能优越，鲁棒性更好。