1. 题目

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但父节点不同，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root，以及树中两个不同节点的值 x 和 y。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true。否则，返回 false。

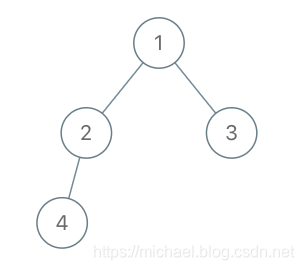
示例 1：
输入：root = [1,2,3,4], x = 4, y = 3
输出：false

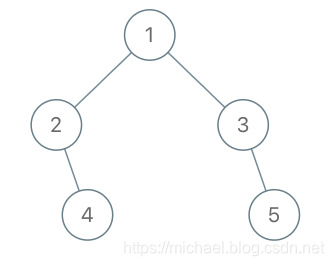
示例 2：
输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true

示例 3：
输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false

提示：
二叉树的节点数介于 2 到 100 之间。
每个节点的值都是唯一的、范围为 1 到 100 的整数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/cousins-in-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

2.1 层序遍历

既然题目要求两节点在同一层，很容易想到层序遍历

• 设置两个bool变量记录x，y出现与否
• 然后遍历过程中，判断每个节点的左右是否同时存在x，y（是否是一个父节点）

class Solution {
public:bool isCousins(TreeNode* root, int x, int y) {queue<TreeNode*> q;TreeNode *tp;q.push(root);int n;bool xOccur = false, yOccur = false;while(!q.empty()){n = q.size();while(n--)//这个循环内是一层的节点{tp = q.front();q.pop();//如果都属于一个父节点，falseif((tp->left && tp->right) && ((tp->left->val == x && tp->right->val == y)|| (tp->left->val == y && tp->right->val == x)))return false;if(tp->val == x)xOccur = true;if(tp->val == y)yOccur = true;if(tp->left)q.push(tp->left);if(tp->right)q.push(tp->right);}//这一层结束了，检查x，y的出现状态if((xOccur^yOccur) == 1)//只有一个出现过了，说明不在一层return false;else if(xOccur && yOccur)//都出现了return true;}return false;}
};

2.2 递归查找

• 题目说了值都是唯一的
• 设置变量记录x,y的父节点和深度，递归查找x,y

class Solution {	TreeNode *pX = NULL, *pY = NULL;//x,y节点的父节点int depX = 0, depY = 0;//x,y节点的深度
public:bool isCousins(TreeNode* root, int x, int y) {findXY(root,x,y,0);if((pX != pY) && (depX == depY))return true;return false;}void findXY(TreeNode* root, int &x, int &y, int dep){if(root == NULL)return;if((root->left && (root->left->val == x))|| (root->right && (root->right->val == x))){pX = root;depX = dep+1;}if((root->left && (root->left->val == y))|| (root->right && (root->right->val == y))){pY = root;depY = dep+1;}findXY(root->left,x,y,dep+1);findXY(root->right,x,y,dep+1);}
};