Q:
请给出一个运行时间为θ(nlgn)的算法,使之能在一个由n个整数构成的集合S和另一个整数X时,判断出S中是否存在有两个其和等于X的元素。
A:
先对S[1 TO N]进行合并排序--------------------------------θ(nlgn)
FOR a <- [1 TO N-1]-------------------------------------n-1
用二分法试图找到b(最坏情况时),使得b+a==x---------θ(nlgn)
所以:
T(n)=θ(nlgn)
时间复杂度小结:
注意,下面函数图像差别是在n很大时,虽然下面n的范围是0-10,但其实这里省去了实际过程中的 c1nlgn与c2n^2的c1和c2,所以差别如此显著
在最坏情况下,插入排序与合并排序的对比:
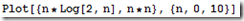
注:高的一条是n^2
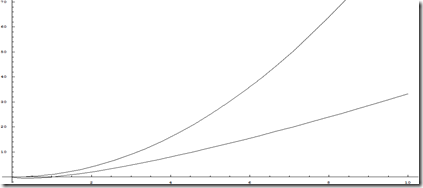
在最好情况下,插入排序时间复杂度θ(n),合并排序时间复杂度θ(nlgn)
注:高的一条为nlgn
另:
插入排序,选择排序:θ(n^2)
合并排序:θ(nlgn)
二分查找:θ(lgn)
)

)
)

)
)

)


)



)


)
)