LeetCode 2212. 射箭比赛中的最大得分（状态枚举）

文章目录

- 1. 题目
- 2. 解题

1. 题目

Alice 和 Bob 是一场射箭比赛中的对手。比赛规则如下：

Alice 先射 numArrows 支箭，然后 Bob 也射 numArrows 支箭。

分数按下述规则计算：

箭靶有若干整数计分区域，范围从 0 到 11 （含 0 和 11）。
箭靶上每个区域都对应一个得分 k（范围是 0 到 11），Alice 和 Bob 分别在得分 k 区域射中 ak 和 bk 支箭。
如果 ak >= bk ，那么 Alice 得 k 分。如果 ak < bk ，则 Bob 得 k 分
如果 ak == bk == 0 ，那么无人得到 k 分。

例如，Alice 和 Bob 都向计分为 11 的区域射 2 支箭，那么 Alice 得 11 分。如果 Alice 向计分为 11 的区域射 0 支箭，但 Bob 向同一个区域射 2 支箭，那么 Bob 得 11 分。

给你整数 numArrows 和一个长度为 12 的整数数组 aliceArrows ，该数组表示 Alice 射中 0 到 11 每个计分区域的箭数量。
现在，Bob 想要尽可能 最大化 他所能获得的总分。

返回数组 bobArrows ，该数组表示 Bob 射中 0 到 11 每个计分区域的箭数量。且 bobArrows 的总和应当等于 numArrows 。

如果存在多种方法都可以使 Bob 获得最大总分，返回其中 任意一种 即可。

示例 1：
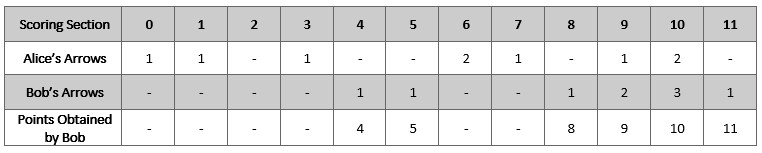
在这里插入图片描述

输入：numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
输出：[0,0,0,0,1,1,0,0,1,2,3,1]
解释：上表显示了比赛得分情况。
Bob 获得总分 4 + 5 + 8 + 9 + 10 + 11 = 47 。
可以证明 Bob 无法获得比 47 更高的分数。

示例 2：
在这里插入图片描述

输入：numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
输出：[0,0,0,0,0,0,0,0,1,1,1,0]
解释：上表显示了比赛得分情况。
Bob 获得总分 8 + 9 + 10 = 27 。
可以证明 Bob 无法获得比 27 更高的分数。提示：
1 <= numArrows <= 10^5
aliceArrows.length == bobArrows.length == 12
0 <= aliceArrows[i], bobArrows[i] <= numArrows
sum(aliceArrows[i]) == numArrows

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-points-in-an-archery-competition
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

用 12位的 int 表示 bob 能赢下来的位置
分别检查需要的箭的数量是否足够，取出得分最大的状态即可

class Solution {
public:vector<int> maximumBobPoints(int numArrows, vector<int>& aliceArrows) {int maxscore = 0, ans_state = 0;for(int state = 1; state < (1<<12); ++state){int needarrows = 0, score = 0;for(int j = 0; j < 12; ++j){if((state>>j)&1) // bob 要取得 j 的得分{needarrows += aliceArrows[j]+1;//至少需要比alice多一个箭score += j;}}if(needarrows <= numArrows && score > maxscore){maxscore = score;ans_state = state;}}vector<int> ans(12, 0);int usedarrows = 0, idx = -1;for(int i = 0; i < 12; ++i){if((ans_state>>i)&1){ans[i] = aliceArrows[i]+1;usedarrows += ans[i];idx = i; // 赢的一个位置}}int leftarrows = numArrows - usedarrows;ans[idx] += leftarrows;//剩余的箭随便找个位置放上return ans;}
};