同学你好!本文章于2021年末编写,已与实际存在较大的偏差!
故在2022年末对本系列进行填充与更新,欢迎大家订阅最新的专栏,获取基于Pytorch1.10版本的理论代码(2023版)实现,
Pytorch深度学习·理论篇(2023版)目录地址为:
CSDN独家 | 全网首发 | Pytorch深度学习·理论篇(2023版)目录本专栏将通过系统的深度学习实例,从可解释性的角度对深度学习的原理进行讲解与分析,通过将深度学习知识与Pytorch的高效结合,帮助各位新入门的读者理解深度学习各个模板之间的关系,这些均是在Pytorch上实现的,可以有效的结合当前各位研究生的研究方向,设计人工智能的各个领域,是经过一年时间打磨的精品专栏!https://v9999.blog.csdn.net/article/details/127587345欢迎大家订阅(2023版)理论篇
以下为2021版原文~~~~
0.导数和微分
0.1逼近法
在2500年前,古希腊人把一个多边形分成三角形,并把它们的面积相加,才找到计算多边形面积的方法。 为了求出曲线形状(比如圆)的面积,古希腊人在这样的形状上刻内接多边形,内接多边形的等长边越多,就越接近圆。这个过程也被称为逼近法。

在深度学习中,我们“训练”模型,不断更新它们,使它们在看到越来越多的数据时变得越来越好。通常情况下,变得更好意味着最小化一个损失函数(loss function),即一个衡量“我们的模型有多糟糕”这个问题的分数。这个问题比看上去要微妙得多。
最终,我们真正关心的是生成一个能够在我们从未见过的数据上表现良好的模型。但我们只能将模型与我们实际能看到的数据相拟合。
因此,我们可以将拟合模型的任务分解为两个关键问题:
(1)优化(optimization):用模型拟合观测数据的过程;
(2)泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。
0.2 导数和微分
在深度学习中,我们通常选择对于模型参数可微的损失函数。这意味着,对于每个参数, 如果我们把这个参数增加或减少一个无穷小的量,我们可以知道损失会以多快的速度增加或减少。

0.2.1 简单模拟求导过程

%matplotlib inline
import numpy as np
from IPython import display
from d2l import torch as d2ldef f(x):return 3 * x ** 2 - 4 * x
def numerical_lim(f, x, h):return (f(x + h) - f(x)) / hh = 0.1
for i in range(5):print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')h *= 0.1h=0.10000, numerical limit=2.30000 h=0.01000, numerical limit=2.03000 h=0.00100, numerical limit=2.00300 h=0.00010, numerical limit=2.00030 h=0.00001, numerical limit=2.00003
1.自动求导









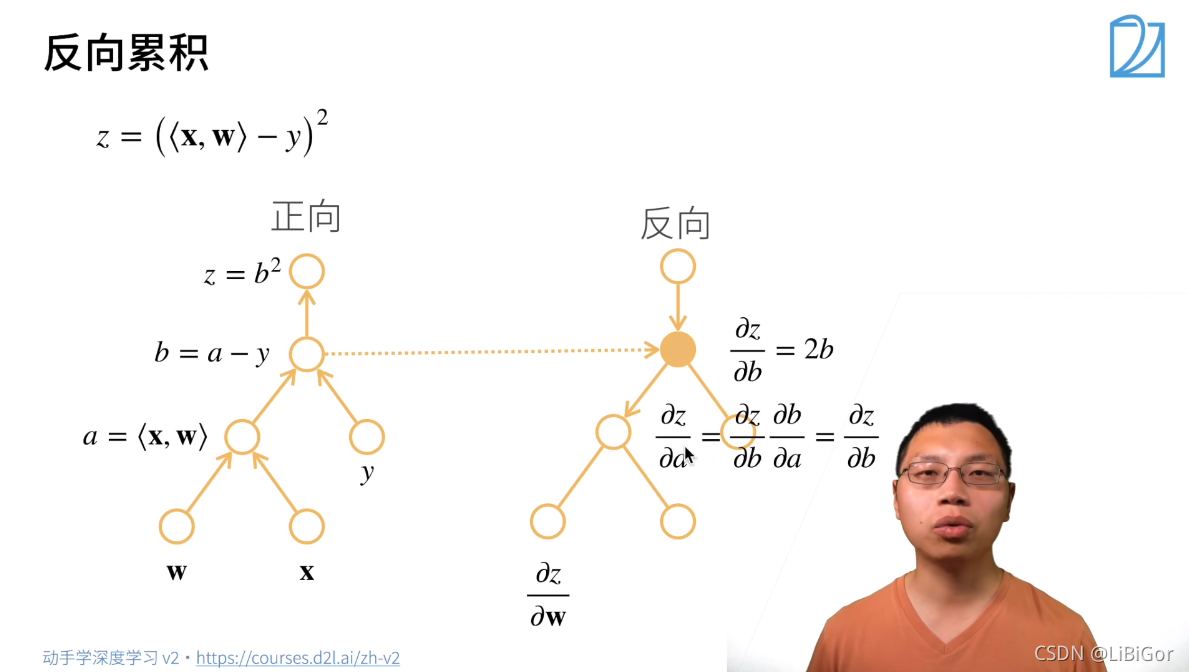
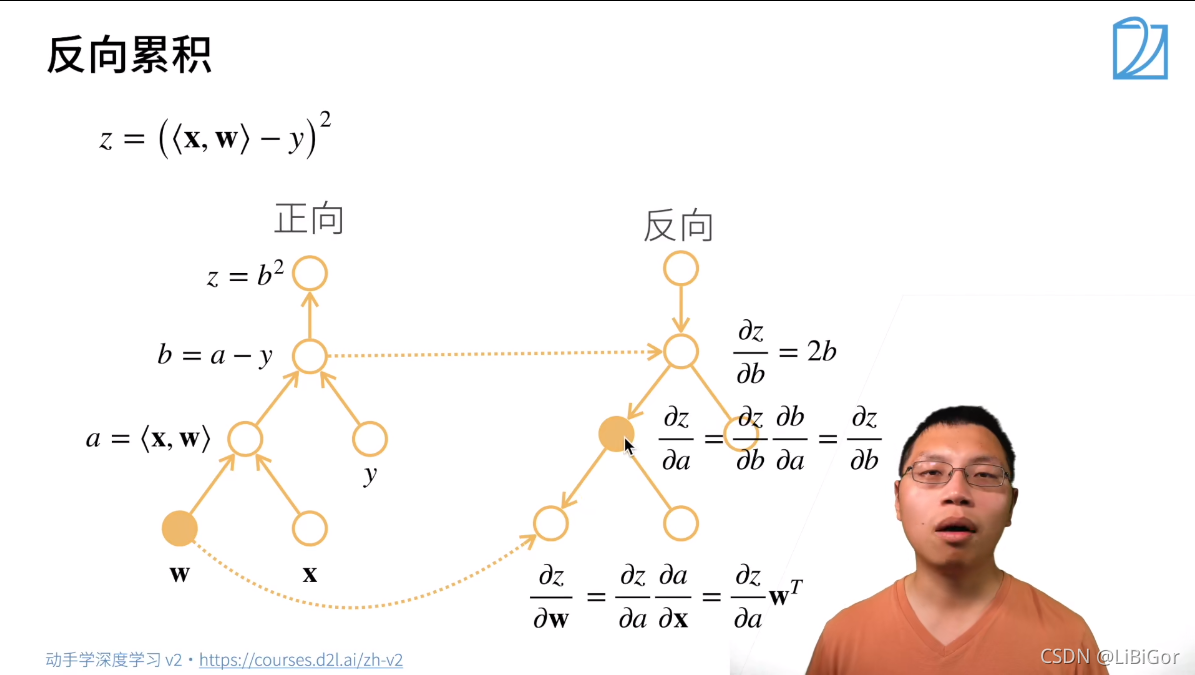


2.自动求导实现
2.1ppt截图







2.2 代码实现
import torchprint('1.自动梯度计算')
x = torch.arange(4.0, requires_grad=True) # 1.将梯度附加到想要对其计算偏导数的变量
print('x:', x)
print('x.grad:', x.grad)1.自动梯度计算 x: tensor([0., 1., 2., 3.], requires_grad=True) x.grad: None
y = 2 * torch.dot(x, x) # 2.记录目标值的计算 对应位置相乘再相加
print('y:', y) y: tensor(28., grad_fn=<MulBackward0>)
y.backward() # 3.y=2*x*x 执行它的反向传播函数
print('x.grad:', x.grad) # 4.访问得到的梯度
print('x.grad == 4*x:', x.grad == 4 * x)x.grad: tensor([ 0., 4., 8., 12.]) x.grad == 4*x: tensor([True, True, True, True])
## 计算另一个函数
x.grad.zero_() #梯度清零
print('x:', x)
y = x.sum()
print('y:', y)
y.backward()
print('x.grad:', x.grad)x: tensor([0., 1., 2., 3.], requires_grad=True) y: tensor(6., grad_fn=<SumBackward0>) x.grad: tensor([1., 1., 1., 1.])
# 非标量变量的反向传播
x.grad.zero_()
print('x:', x)
y = x * x
y.sum().backward()
print('x.grad:', x.grad)x: tensor([0., 1., 2., 3.], requires_grad=True) x.grad: tensor([0., 2., 4., 6.])
def f(a):b = a * 2print(b.norm())print("开始循环:")while b.norm() < 1000: # 求L2范数:元素平方和的平方根b = b * 2print(b)print("开始判断")if b.sum() > 0:c = belse:c = 100 * breturn c
print('2.Python控制流的梯度计算')
a = torch.tensor(2.0) # 初始化变量
print(a)
a.requires_grad_(True) # 1.将梯度赋给想要对其求偏导数的变量
print('a:', a)
d = f(a) # 2.记录目标函数
print('d:', d)
d.backward() # 3.执行目标函数的反向传播函数
print('a.grad:', a.grad) # 4.获取梯度2.Python控制流的梯度计算 tensor(2.) a: tensor(2., requires_grad=True) tensor(4., grad_fn=<CopyBackwards>) 开始循环: tensor(8., grad_fn=<MulBackward0>) tensor(16., grad_fn=<MulBackward0>) tensor(32., grad_fn=<MulBackward0>) tensor(64., grad_fn=<MulBackward0>) tensor(128., grad_fn=<MulBackward0>) tensor(256., grad_fn=<MulBackward0>) tensor(512., grad_fn=<MulBackward0>) tensor(1024., grad_fn=<MulBackward0>) 开始判断 d: tensor(1024., grad_fn=<MulBackward0>) a.grad: tensor(512.)
QA
1.显示构造:先将整个计算写出来,再去写入参数值。
2.在深度网络求梯度的时候,需要正向算一遍(将y的函数值算出来),反向算一遍。
3.pytorch默认累计梯度的原因:累计梯度的情况主要是在批量的情况下,Pytorch对于内存的管理不够好,批量计算的内存大小较大,因此将其分开计算,故需要默认累计梯度。
4.为什么深度学习中一般都去标量求导,而不是对矩阵和向量,如果我的loss是包含向量或矩阵的情况下,在求导之前是否需要将其变成标量的形式?
答:loss通常是一个标量
5.多个loss分别反向的情况下,需要累计梯度
6.为什么获取grad前需要backward?
因为backward占用内存较大
7.pytorch上可以实现矢量求导吗?
可以,高阶求导,但是通常需要优化算法。
在PyTorch中data.norm()是含义_Escape the bug的博客-CSDN博客https://blog.csdn.net/jnbfknasf113/article/details/110141537![]() https://blog.csdn.net/jnbfknasf113/article/details/110141537
https://blog.csdn.net/jnbfknasf113/article/details/110141537




)















