sklearn官网-多分类问题

sklearn实战-乳腺癌细胞数据挖掘（博主亲自录制视频）

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

 

 

1.12.6. Multioutput classification

Multioutput classification support can be added to any classifier with MultiOutputClassifier. This strategy consists of fitting one classifier per target. This allows multiple target variable classifications. The purpose of this class is to extend estimators to be able to estimate a series of target functions (f1,f2,f3…,fn) that are trained on a single X predictor matrix to predict a series of responses (y1,y2,y3…,yn).

Below is an example of multioutput classification:

>>>

from sklearn.datasets import make_classification
from sklearn.multioutput import MultiOutputClassifier from sklearn.ensemble import RandomForestClassifier from sklearn.utils import shuffle import numpy as np X, y1 = make_classification(n_samples=10, n_features=100, n_informative=30, n_classes=3, random_state=1) y2 = shuffle(y1, random_state=1) y3 = shuffle(y1, random_state=2) Y = np.vstack((y1, y2, y3)).T n_samples, n_features = X.shape # 10,100 n_outputs = Y.shape[1] # 3 n_classes = 3 forest = RandomForestClassifier(n_estimators=100, random_state=1) multi_target_forest = MultiOutputClassifier(forest, n_jobs=-1) multi_target_forest.fit(X, Y).predict(X)

 

1.12. Multiclass and multilabel algorithms

Warning

 

All classifiers in scikit-learn do multiclass classification out-of-the-box. You don’t need to use thesklearn.multiclass module unless you want to experiment with different multiclass strategies.

The sklearn.multiclass module implements meta-estimators to solve multiclass and multilabel classification problems by decomposing such problems into binary classification problems. Multitarget regression is also supported.

• Multiclass classification means a classification task with more than two classes; e.g., classify a set of images of fruits which may be oranges, apples, or pears. Multiclass classification makes the assumption that each sample is assigned to one and only one label: a fruit can be either an apple or a pear but not both at the same time.

• Multilabel classification assigns to each sample a set of target labels. This can be thought as predicting properties of a data-point that are not mutually exclusive, such as topics that are relevant for a document. A text might be about any of religion, politics, finance or education at the same time or none of these.

• Multioutput regression assigns each sample a set of target values. This can be thought of as predicting several properties for each data-point, such as wind direction and magnitude at a certain location.

• Multioutput-multiclass classification and multi-task classification means that a single estimator has to handle several joint classification tasks. This is both a generalization of the multi-label classification task, which only considers binary classification, as well as a generalization of the multi-class classification task. The output format is a 2d numpy array or sparse matrix.

  The set of labels can be different for each output variable. For instance, a sample could be assigned “pear” for an output variable that takes possible values in a finite set of species such as “pear”, “apple”; and “blue” or “green” for a second output variable that takes possible values in a finite set of colors such as “green”, “red”, “blue”, “yellow”…

  This means that any classifiers handling multi-output multiclass or multi-task classification tasks, support the multi-label classification task as a special case. Multi-task classification is similar to the multi-output classification task with different model formulations. For more information, see the relevant estimator documentation.

All scikit-learn classifiers are capable of multiclass classification, but the meta-estimators offered by sklearn.multiclasspermit changing the way they handle more than two classes because this may have an effect on classifier performance (either in terms of generalization error or required computational resources).

Below is a summary of the classifiers supported by scikit-learn grouped by strategy; you don’t need the meta-estimators in this class if you’re using one of these, unless you want custom multiclass behavior:

• Inherently multiclass:
  • sklearn.naive_bayes.BernoulliNB
  • sklearn.tree.DecisionTreeClassifier
  • sklearn.tree.ExtraTreeClassifier
  • sklearn.ensemble.ExtraTreesClassifier
  • sklearn.naive_bayes.GaussianNB
  • sklearn.neighbors.KNeighborsClassifier
  • sklearn.semi_supervised.LabelPropagation
  • sklearn.semi_supervised.LabelSpreading
  • sklearn.discriminant_analysis.LinearDiscriminantAnalysis
  • sklearn.svm.LinearSVC (setting multi_class=”crammer_singer”)
  • sklearn.linear_model.LogisticRegression (setting multi_class=”multinomial”)
  • sklearn.linear_model.LogisticRegressionCV (setting multi_class=”multinomial”)
  • sklearn.neural_network.MLPClassifier
  • sklearn.neighbors.NearestCentroid
  • sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis
  • sklearn.neighbors.RadiusNeighborsClassifier
  • sklearn.ensemble.RandomForestClassifier
  • sklearn.linear_model.RidgeClassifier
  • sklearn.linear_model.RidgeClassifierCV
• Multiclass as One-Vs-One:
  • sklearn.svm.NuSVC
  • sklearn.svm.SVC.
  • sklearn.gaussian_process.GaussianProcessClassifier (setting multi_class = “one_vs_one”)
• Multiclass as One-Vs-All:
  • sklearn.ensemble.GradientBoostingClassifier
  • sklearn.gaussian_process.GaussianProcessClassifier (setting multi_class = “one_vs_rest”)
  • sklearn.svm.LinearSVC (setting multi_class=”ovr”)
  • sklearn.linear_model.LogisticRegression (setting multi_class=”ovr”)
  • sklearn.linear_model.LogisticRegressionCV (setting multi_class=”ovr”)
  • sklearn.linear_model.SGDClassifier
  • sklearn.linear_model.Perceptron
  • sklearn.linear_model.PassiveAggressiveClassifier
• Support multilabel:
  • sklearn.tree.DecisionTreeClassifier
  • sklearn.tree.ExtraTreeClassifier
  • sklearn.ensemble.ExtraTreesClassifier
  • sklearn.neighbors.KNeighborsClassifier
  • sklearn.neural_network.MLPClassifier
  • sklearn.neighbors.RadiusNeighborsClassifier
  • sklearn.ensemble.RandomForestClassifier
  • sklearn.linear_model.RidgeClassifierCV
• Support multiclass-multioutput:
  • sklearn.tree.DecisionTreeClassifier
  • sklearn.tree.ExtraTreeClassifier
  • sklearn.ensemble.ExtraTreesClassifier
  • sklearn.neighbors.KNeighborsClassifier
  • sklearn.neighbors.RadiusNeighborsClassifier
  • sklearn.ensemble.RandomForestClassifier

Warning

 

At present, no metric in sklearn.metrics supports the multioutput-multiclass classification task.

1.12.1. Multilabel classification format

In multilabel learning, the joint set of binary classification tasks is expressed with label binary indicator array: each sample is one row of a 2d array of shape (n_samples, n_classes) with binary values: the one, i.e. the non zero elements, corresponds to the subset of labels. An array such as np.array([[1, 0, 0], [0, 1, 1], [0, 0, 0]]) represents label 0 in the first sample, labels 1 and 2 in the second sample, and no labels in the third sample.

Producing multilabel data as a list of sets of labels may be more intuitive. The MultiLabelBinarizer transformer can be used to convert between a collection of collections of labels and the indicator format.

>>>

>>> from sklearn.preprocessing import MultiLabelBinarizer >>> y = [[2, 3, 4], [2], [0, 1, 3], [0, 1, 2, 3, 4], [0, 1, 2]] >>> MultiLabelBinarizer().fit_transform(y) array([[0, 0, 1, 1, 1],  [0, 0, 1, 0, 0],  [1, 1, 0, 1, 0],  [1, 1, 1, 1, 1],  [1, 1, 1, 0, 0]]) 

1.12.2. One-Vs-The-Rest

This strategy, also known as one-vs-all, is implemented in OneVsRestClassifier. The strategy consists in fitting one classifier per class. For each classifier, the class is fitted against all the other classes. In addition to its computational efficiency (only n_classes classifiers are needed), one advantage of this approach is its interpretability. Since each class is represented by one and only one classifier, it is possible to gain knowledge about the class by inspecting its corresponding classifier. This is the most commonly used strategy and is a fair default choice.

1.12.2.1. Multiclass learning

Below is an example of multiclass learning using OvR:

>>>

>>> from sklearn import datasets >>> from sklearn.multiclass import OneVsRestClassifier >>> from sklearn.svm import LinearSVC >>> iris = datasets.load_iris() >>> X, y = iris.data, iris.target >>> OneVsRestClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X) array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,  0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,  1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1,  1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2,  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) 

1.12.2.2. Multilabel learning

OneVsRestClassifier also supports multilabel classification. To use this feature, feed the classifier an indicator matrix, in which cell [i, j] indicates the presence of label j in sample i.

Examples:

• Multilabel classification

1.12.3. One-Vs-One

OneVsOneClassifier constructs one classifier per pair of classes. At prediction time, the class which received the most votes is selected. In the event of a tie (among two classes with an equal number of votes), it selects the class with the highest aggregate classification confidence by summing over the pair-wise classification confidence levels computed by the underlying binary classifiers.

Since it requires to fit n_classes * (n_classes - 1) / 2 classifiers, this method is usually slower than one-vs-the-rest, due to its O(n_classes^2) complexity. However, this method may be advantageous for algorithms such as kernel algorithms which don’t scale well with n_samples. This is because each individual learning problem only involves a small subset of the data whereas, with one-vs-the-rest, the complete dataset is used n_classes times.

1.12.3.1. Multiclass learning

Below is an example of multiclass learning using OvO:

>>>

>>> from sklearn import datasets >>> from sklearn.multiclass import OneVsOneClassifier >>> from sklearn.svm import LinearSVC >>> iris = datasets.load_iris() >>> X, y = iris.data, iris.target >>> OneVsOneClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X) array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,  0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,  1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1,  1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) 

References:

• “Pattern Recognition and Machine Learning. Springer”, Christopher M. Bishop, page 183, (First Edition)

1.12.4. Error-Correcting Output-Codes

Output-code based strategies are fairly different from one-vs-the-rest and one-vs-one. With these strategies, each class is represented in a Euclidean space, where each dimension can only be 0 or 1. Another way to put it is that each class is represented by a binary code (an array of 0 and 1). The matrix which keeps track of the location/code of each class is called the code book. The code size is the dimensionality of the aforementioned space. Intuitively, each class should be represented by a code as unique as possible and a good code book should be designed to optimize classification accuracy. In this implementation, we simply use a randomly-generated code book as advocated in [3] although more elaborate methods may be added in the future.

At fitting time, one binary classifier per bit in the code book is fitted. At prediction time, the classifiers are used to project new points in the class space and the class closest to the points is chosen.

In OutputCodeClassifier, the code_size attribute allows the user to control the number of classifiers which will be used. It is a percentage of the total number of classes.

A number between 0 and 1 will require fewer classifiers than one-vs-the-rest. In theory, log2(n_classes) / n_classes is sufficient to represent each class unambiguously. However, in practice, it may not lead to good accuracy since log2(n_classes) is much smaller than n_classes.

A number greater than 1 will require more classifiers than one-vs-the-rest. In this case, some classifiers will in theory correct for the mistakes made by other classifiers, hence the name “error-correcting”. In practice, however, this may not happen as classifier mistakes will typically be correlated. The error-correcting output codes have a similar effect to bagging.

1.12.4.1. Multiclass learning

Below is an example of multiclass learning using Output-Codes:

>>>

>>> from sklearn import datasets >>> from sklearn.multiclass import OutputCodeClassifier >>> from sklearn.svm import LinearSVC >>> iris = datasets.load_iris() >>> X, y = iris.data, iris.target >>> clf = OutputCodeClassifier(LinearSVC(random_state=0), ... code_size=2, random_state=0) >>> clf.fit(X, y).predict(X) array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,  0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,  0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1,  1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1,  1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,  2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2,  2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) 

References:

• “Solving multiclass learning problems via error-correcting output codes”, Dietterich T., Bakiri G., Journal of Artificial Intelligence Research 2, 1995.

[3]	“The error coding method and PICTs”, James G., Hastie T., Journal of Computational and Graphical statistics 7, 1998.

• “The Elements of Statistical Learning”, Hastie T., Tibshirani R., Friedman J., page 606 (second-edition) 2008.

1.12.5. Multioutput regression

Multioutput regression support can be added to any regressor with MultiOutputRegressor. This strategy consists of fitting one regressor per target. Since each target is represented by exactly one regressor it is possible to gain knowledge about the target by inspecting its corresponding regressor. As MultiOutputRegressor fits one regressor per target it can not take advantage of correlations between targets.

Below is an example of multioutput regression:

>>>

>>> from sklearn.datasets import make_regression >>> from sklearn.multioutput import MultiOutputRegressor >>> from sklearn.ensemble import GradientBoostingRegressor >>> X, y = make_regression(n_samples=10, n_targets=3, random_state=1) >>> MultiOutputRegressor(GradientBoostingRegressor(random_state=0)).fit(X, y).predict(X) array([[-154.75474165, -147.03498585, -50.03812219],  [ 7.12165031, 5.12914884, -81.46081961],  [-187.8948621 , -100.44373091, 13.88978285],  [-141.62745778, 95.02891072, -191.48204257],  [ 97.03260883, 165.34867495, 139.52003279],  [ 123.92529176, 21.25719016, -7.84253 ],  [-122.25193977, -85.16443186, -107.12274212],  [ -30.170388 , -94.80956739, 12.16979946],  [ 140.72667194, 176.50941682, -17.50447799],  [ 149.37967282, -81.15699552, -5.72850319]]) 

1.12.6. Multioutput classification

Multioutput classification support can be added to any classifier with MultiOutputClassifier. This strategy consists of fitting one classifier per target. This allows multiple target variable classifications. The purpose of this class is to extend estimators to be able to estimate a series of target functions (f1,f2,f3…,fn) that are trained on a single X predictor matrix to predict a series of responses (y1,y2,y3…,yn).

Below is an example of multioutput classification:

>>>

>>> from sklearn.datasets import make_classification >>> from sklearn.multioutput import MultiOutputClassifier >>> from sklearn.ensemble import RandomForestClassifier >>> from sklearn.utils import shuffle >>> import numpy as np >>> X, y1 = make_classification(n_samples=10, n_features=100, n_informative=30, n_classes=3, random_state=1) >>> y2 = shuffle(y1, random_state=1) >>> y3 = shuffle(y1, random_state=2) >>> Y = np.vstack((y1, y2, y3)).T >>> n_samples, n_features = X.shape # 10,100 >>> n_outputs = Y.shape[1] # 3 >>> n_classes = 3 >>> forest = RandomForestClassifier(n_estimators=100, random_state=1) >>> multi_target_forest = MultiOutputClassifier(forest, n_jobs=-1) >>> multi_target_forest.fit(X, Y).predict(X) array([[2, 2, 0],  [1, 2, 1],  [2, 1, 0],  [0, 0, 2],  [0, 2, 1],  [0, 0, 2],  [1, 1, 0],  [1, 1, 1],  [0, 0, 2],  [2, 0, 0]]) 

1.12.7. Classifier Chain

Classifier chains (see ClassifierChain) are a way of combining a number of binary classifiers into a single multi-label model that is capable of exploiting correlations among targets.

For a multi-label classification problem with N classes, N binary classifiers are assigned an integer between 0 and N-1. These integers define the order of models in the chain. Each classifier is then fit on the available training data plus the true labels of the classes whose models were assigned a lower number.

When predicting, the true labels will not be available. Instead the predictions of each model are passed on to the subsequent models in the chain to be used as features.

Clearly the order of the chain is important. The first model in the chain has no information about the other labels while the last model in the chain has features indicating the presence of all of the other labels. In general one does not know the optimal ordering of the models in the chain so typically many randomly ordered chains are fit and their predictions are averaged together.

References:

Jesse Read, Bernhard Pfahringer, Geoff Holmes, Eibe Frank,

“Classifier Chains for Multi-label Classification”, 2009.

1.12.8. Regressor Chain

Regressor chains (see RegressorChain) is analogous to ClassifierChain as a way of combining a number of regressions into a single multi-target model that is capable of exploiting correlations among targets.

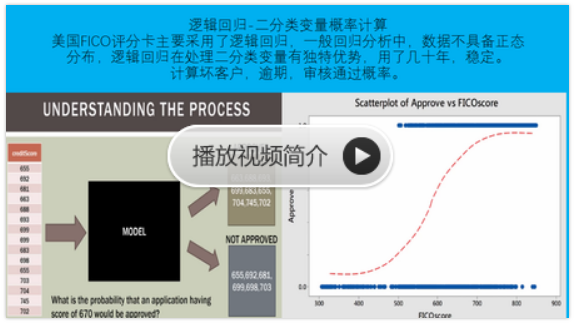
python风控评分卡建模和风控常识

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share