Coursera自动驾驶课程第14讲：Linear and Nonlinear Kalman Filters

在上一讲《Coursera自动驾驶课程第13讲：Least Squares》我们学习了最小二乘法相关知识。

本讲我们将学习20世纪最著名的一个算法：卡尔曼滤波。具体包括线性卡尔曼滤波（KF），扩展卡尔曼滤波(EKF)，误差状态卡尔曼滤波（ES-EKF）以及无损卡尔曼滤波（UKF）。

B站视频链接：https://www.bilibili.com/video/BV1cE411D7Y9。

1. Kalman Filter

1.1 Overview

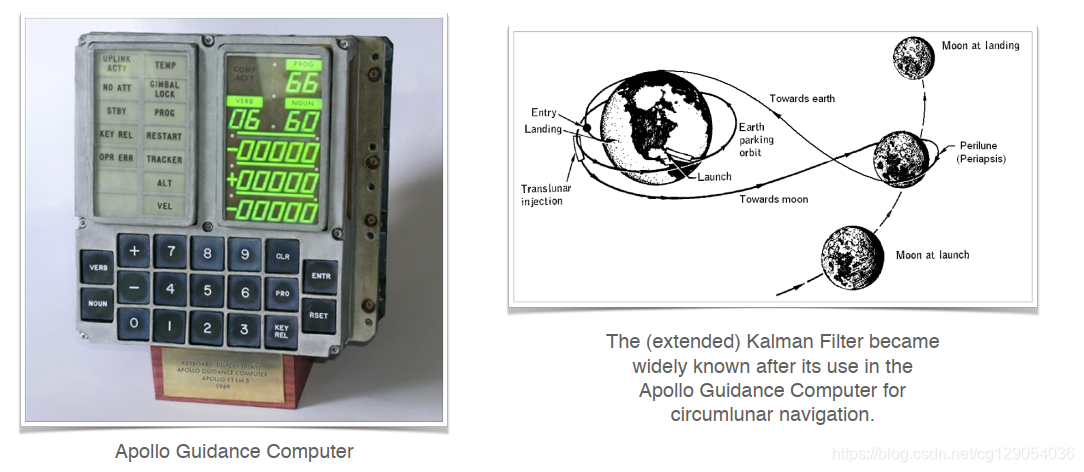
我们先介绍一个关于卡尔曼滤波算法的故事。卡尔曼滤波算法是由匈牙利教授和工程师Rudolf E. Kalman于1960年提出的，他曾在马里兰州巴尔的摩的高级研究所工作。2009年，美国总统Barack Obama授予卡尔曼教授美国国家科学奖章，以表彰他在卡尔曼滤波器和在控制工程领域的贡献。

1960年发布后，卡尔曼滤波算法被NASA应用于阿波罗制导计算机。这项突破性的创新在阿波罗号登月中发挥了关键作用。该滤波器有助于将阿波罗号航天飞船精确地通过绕月轨道。

（这里有一篇国外介绍的卡尔曼滤波器推导与解析的文章：博文。）

1.2 Prediction and Correction

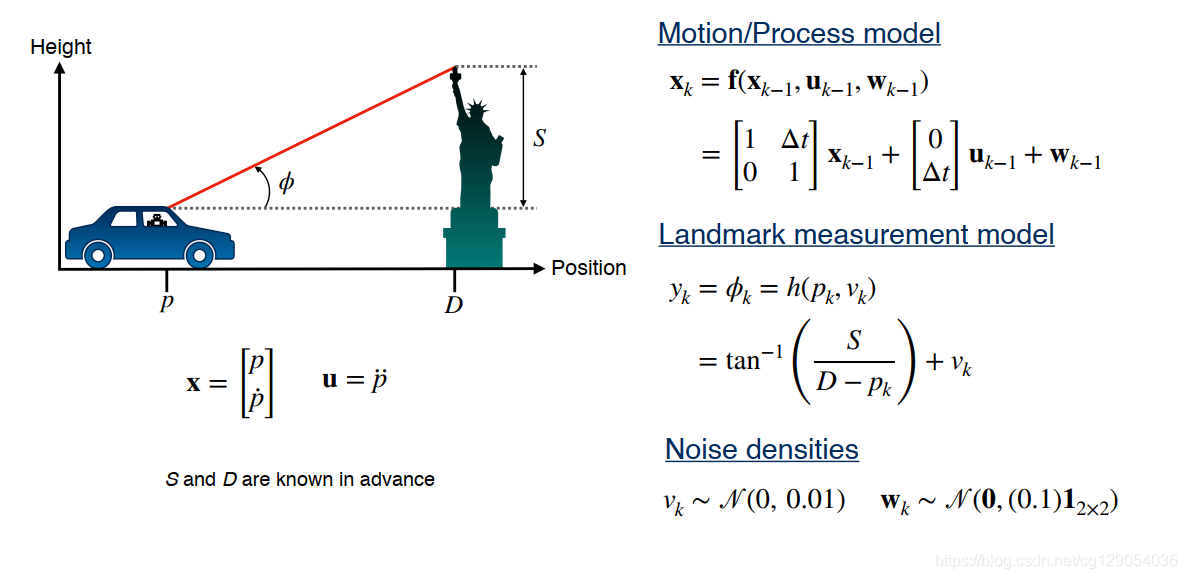
卡尔曼滤波器与我们上一讲讨论的线性递归最小二乘滤波器非常相似。递归最小二乘可以更新参数的估计值，但卡尔曼滤波器却能够对状态量进行估计和更新。卡尔曼滤波器的目标是对该状态量进行概率估计，主要是分两步实时更新：预测和修正。下面让我们来看一个估计汽车位置的问题。
在这里插入图片描述

从时间 $k - 1$ 时的初始概率估计开始，我们的目的是使用从车轮里程计或惯性传感器测量得出的数据并使用运动模型来预测汽车的位置。
然后，我们使用从 GPS或Lidar 测量得出的数据并使用测量模型来修正 $k$ 时刻汽车的位置。这里，我们可以将卡尔曼滤波器视为一种融合来自不同传感器的信息对未知状态进行最终估计的技术，并同时考虑到运动和测量模型中的不确定性。

1.3 Linear Dynamical System

对于卡尔曼滤波算法，我们先定义汽车的运动模型：

$xk=Fk−1xk−1+Gk−1uk−1+wk−1\mathbf{x_k} = \mathbf{F_{k-1}}\mathbf{x_{k-1}} + \mathbf{G_{k-1}}\mathbf{u_{k-1}}+\mathbf{w_{k-1}}$

其中： $Fk−1\mathbf{F_{k-1}}$ 是系统状态转移矩阵， $GK−1\mathbf{G_{K-1}}$ 是系统控制矩阵， $uk\mathbf{u_k}$ 是系统输入信号， $wk−1\mathbf{w_{k-1}}$ 为过程噪声。

然后定义我们的测量模型：
$yk=Hkxk+vk\mathbf{y_k}=\mathbf{H_k}\mathbf{x_k}+\mathbf{v_k}$

其中： $Hk\mathbf{H_k}$ 是测量矩阵， $vk\mathbf{v_k}$ 是测量噪声。

现在介绍卡尔曼滤波是如何工作的，卡尔曼滤波器与递归最小二乘估计器很相似，不过其包含一个运动模型。
在这里插入图片描述

首先，我们使用运动模型来预测，预测公式如下：
$xˇk=Fk−1xk−1+Gk−1uk−1Pˇk=Fk−1P^k−1Fk−1T+Qk−1\begin{aligned} \check{\mathbf{x}}_{k} &=\mathbf{F}_{k-1} \mathbf{x}_{k-1}+\mathbf{G}_{k-1} \mathbf{u}_{k-1} \\ \check{\mathbf{P}}_{k} &=\mathbf{F}_{k-1} \hat{\mathbf{P}}_{k-1} \mathbf{F}_{k-1}^{T}+\mathbf{Q}_{k-1} \end{aligned}$
然后，我们计算卡尔曼增益：
$Kk=PˇkHkT(HkPˇkHkT+Rk)−1\mathbf{K}_{k}=\check{\mathbf{P}}_{k} \mathbf{H}_{k}^{T}\left(\mathbf{H}_{k} \check{\mathbf{P}}_{k} \mathbf{H}_{k}^{T}+\mathbf{R}_{k}\right)^{-1}$
最后，修正系统状态量和协方差矩阵：
$x^k=xˇk+Kk(yk−Hkxˇk)P^k=(I−KkHk)Pˇk\begin{aligned} \hat{\mathbf{x}}_{k} &=\check{\mathbf{x}}_{k}+\mathbf{K}_{k}\left(\mathbf{y}_{k}-\mathbf{H}_{k} \check{\mathbf{x}}_{k}\right) \\ \hat{\mathbf{P}}_{k} &=\left(\mathbf{I}-\mathbf{K}_{k} \mathbf{H}_{k}\right) \check\mathbf{P}_{k} \end{aligned}$

最后我们来看一个估计汽车一维位置的例子：

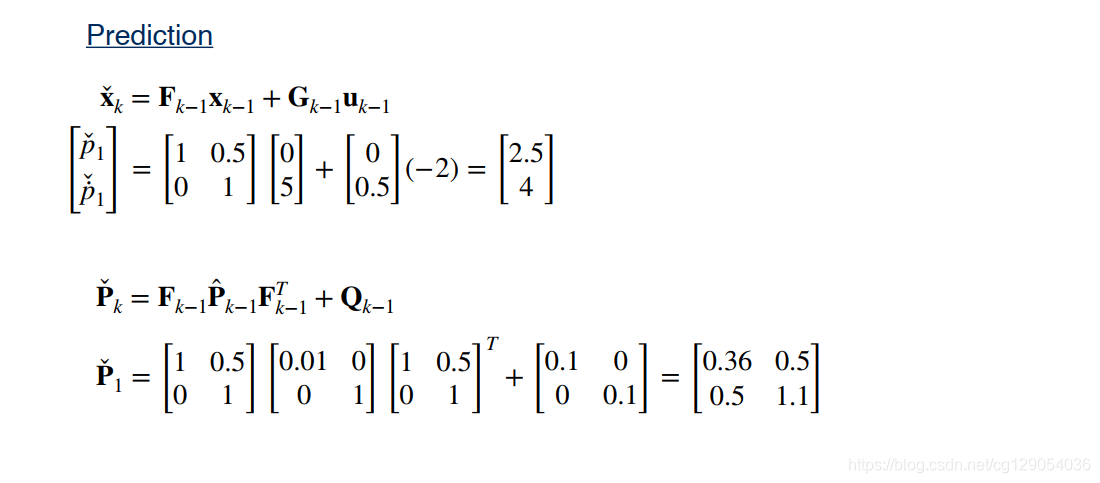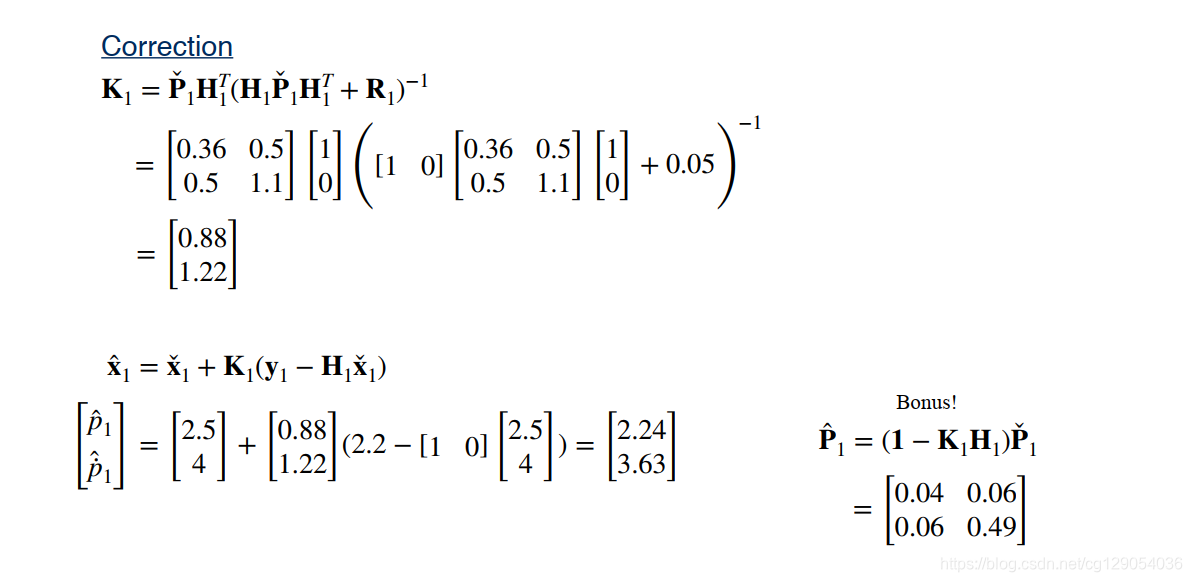2. Kalman Filter：Bias BLUES

2.1 Bias in State Estimation

上一小节，我们介绍了卡尔曼滤波器，这一节让我们讨论一下卡尔曼滤波算法为什么如此诱人。

首先，让我们讨论Bias。我们使用上一小节中的卡尔曼滤波器来估计自动驾驶汽车的位置。如果我们有某种方式知道车辆的真实位置，那么我们可以使用它来记录在 $k$ 时刻的滤波器位置误差。从图形上看，情况可能是这样。在时刻 $k$ ，我们知道汽车的真正位置。我们在多个试验中建立位置直方图，然后计算这些估计值的平均值与真实位置之间的差。如果差不为零，则我们的估计存在偏差。但是，如果当我们多次重复该实验时位置偏差接近于零，并且如果在所有时刻都发生这种情况，则可以说我们的滤波器是无偏的。

用公式表达则为：
$E[e^k]=E[p^k−pk]=E[p^k]−pk=0E\left[\hat{e}_{k}\right]=E\left[\hat{p}_{k}-p_{k}\right]=E\left[\hat{p}_{k}\right]-p_{k}=0$

在这里插入图片描述
现在让我们从理论上分析卡尔曼滤波为什么是无偏的，我们先考虑滤波器误差动态：

预测状态误差： $eˇk=xˇk−xk\check{\mathbf{e}}_{k}=\check{\mathbf{x}}_{k}-\mathbf{x}_{k}$
修正状态误差： $e^k=x^k−xk\hat{\mathbf{e}}_{k}=\hat{\mathbf{x}}_{k}-\mathbf{x}_{k}$
定义了预测和修正后的状态误差，我们可以得到下面的数学方程：
$eˇk=Fk−1eˇk−1−wke^k=(1−KkHk)eˇk+Kkvk\begin{aligned} \check{\mathbf{e}}_{k} &=\mathbf{F}_{k-1} \check{\mathbf{e}}_{k-1}-\mathbf{w}_{k} \\ \hat{\mathbf{e}}_{k} &=\left(\mathbf{1}-\mathbf{K}_{k} \mathbf{H}_{k}\right) \check{\mathbf{e}}_{k}+\mathbf{K}_{k} \mathbf{v}_{k} \end{aligned}$

对于卡尔曼滤波器，我们可以验证误差的期望值正好等于零。为了做到这一点，我们需要确保我们的初始状态估计没有误差即： $E[e^0]=0\mathbf{E[{\hat{e}_0}]}=0$ ，并且我们的噪声均值为零且不相关。

在这里插入图片描述
尽管这对于线性系统来说是一个理想的结果，但请记住，这不能保证我们的估计对于给定的试验将是无误差的，只是误差的期望值为零。

2.2 Consistency in State Estimation

卡尔曼滤波器也具有一致性。一致性是指对于所有时刻，滤波器协方差状态 $P_k$ 与误差平方的期望值一致，数学表达为：

$E[e^k2]=E[(p^k−pk)2]=P^kE\left[\hat{e}_{k}^{2}\right]=E\left[\left(\hat{p}_{k}-p_{k}\right)^{2}\right]=\hat{P}_{k}$
在这里插入图片描述
这里也可以证明对于所有时刻 $k$ ，只需要满足： $E[e^0e^0T]=Pˇ0E[v]=0E[w]=0E\left[\hat{\mathbf{e}}_{0} \hat{\mathbf{e}}_{0}^{T}\right]=\check{\mathbf{P}}_{0} \quad E[\mathbf{v}]=\mathbf{0} \quad E[\mathbf{w}]=\mathbf{0}$ 。则： $E[eˇkeˇkT]=Pˇk,E[e^ke^kT]=P^kE\left[\check\mathbf{e}_{k} \check{\mathbf{e}}_{k}^{T}\right]=\check{\mathbf{P}}_{k} ,E\left[\hat{\mathbf{e}}_{k} \hat{\mathbf{e}}_{k}^{T}\right]=\hat{\mathbf{P}}_{k}$

2.3 Best Linear Unbiased Estimator

综上所述，我们已经证明，在噪声期望为零则不相关的情况下，卡尔曼滤波器是无偏且一致的，即满足以下数学关系：

$E[e^k]=0E[e^ke^kT]=P^kE\left[\hat{e}_{k}\right]=0 \\ E\left[\hat\mathbf{e}_{k} \hat{\mathbf{e}}_{k}^{T}\right]=\hat{\mathbf{P}}_{k}$

通常，如果我们有白色不相关的零期望噪声，则卡尔曼滤波器是最好的（即最低方差）无偏估计滤波器，它以最小的方差进行无偏估计。

3. Extended Kalman Filter

3.1 Overview

到目前为止，在本讲中，我们已经学习了如何使用线性卡尔曼滤波器进行状态估计，并且还证明了卡尔曼滤波器是最佳的线性无偏估计器。但是，线性卡尔曼滤波器不能直接用于估计测量或输入为非线性函数的状态量。为了对非线性系统进行状态估计，我们将学习一种称为扩展卡尔曼滤波的状态估计算法。

我们先回顾线性卡尔曼滤波器的工作原理：
在这里插入图片描述

根据先前的状态以及我们提供给系统的任何输入（例如油门踏板位置），在某个时刻 $k$ 预测更新后的状态估计值和协方差。
然后，线性卡尔曼滤波器使用一个测量模型，将预测值与实际从传感器获得的测量值进行相减。卡尔曼增益告诉我们如何加权这些信息，以便我们可以对它们进行组合并修正状态估计值，得到更新后的状态和协方差。

正如我们在上一小节看到的那样，卡尔曼滤波器实际上是所有线性系统估计器中的最优估计器。不幸的是，在现实世界中线性系统实际上并不存在。

在第一小节我们看到了一个测量电阻的示例，在一定电压范围内，电流与电压存在线性关系，并且遵循欧姆定律。但是，随着电压升高，电阻发热，电阻将会发生改变，电流与电压不再为线性关系。由于我们在实际中遇到的系统是非线性的，因此这里提出了一个重要的问题：我们是否仍然可以将卡尔曼滤波器用于非线性系统？ 在这里插入图片描述

3.2 Linearizing a Nonlinear System

扩展卡尔曼滤波的关键是线性化非线性系统，这里需要用到高等数学里的泰勒展开式。如下图所示的函数 $f (x)$ ，在函数上的某个点 $a$ ，找到点 $a$ 附近的非线性函数的线性近似，即当 $x = a$ 时找到函数 $f (x)$ 的切线，泰勒展开后通常只保留一阶部分，略去高阶部分，如下式所示：
$f(x)≈f(a)+∂f(x)∂x∣x=a(x−a)+12!∂2f(x)∂x2∣x=a(x−a)2+13!∂2f(x)∂x2∣x=a(x−a)3+…f(x)\approx f(a)+\left.\frac{\partial f(x)}{\partial x}\right|_{x=a}(x-a)+\left.\frac{1}{2 !} \frac{\partial^{2} f(x)}{\partial x^{2}}\right|_{x=a}(x-a)^{2}+\left.\frac{1}{3 !} \frac{\partial^{2} f(x)}{\partial x^{2}}\right|_{x=a}(x-a)^{3}+\ldots$
在这里插入图片描述
现在让我们回到非线性系统运动模型和测量模型，并对它们进行线性化处理。我们应该选择哪个点作为泰勒展开点？理想情况下，我们希望线性化关于状态真实值的模型，但是我们不能这样做，因为如果我们已经知道状态的真实值，那就无需再估算了。因此，让我们选择状态的最新估计值作为泰勒展开点。
$xk=fk−1(xk−1,uk−1,wk−1)≈fk−1(x^k−1,uk−1,0)+∂fk−1∂xk−1∣x^k−1,uk−1,0⏟Fk−1(xk−1−x^k−1)+∂fk−1∂wk−1∣x^k−1,uk−1,0⏟Lk−1wk−1\mathbf{x}_{k}=\mathbf{f}_{k-1}\left(\mathbf{x}_{k-1}, \mathbf{u}_{k-1}, \mathbf{w}_{k-1}\right) \approx \mathbf{f}_{k-1}\left(\hat{\mathbf{x}}_{k-1}, \mathbf{u}_{k-1}, \mathbf{0}\right)+\underbrace{\left.\frac{\partial \mathbf{f}_{k-1}}{\partial \mathbf{x}_{k-1}}\right|_{\hat{\mathbf{x}}_{k-1}, \mathbf{u}_{k-1}, \mathbf{0}}}_{\mathbf{F}_{k-1}}\left(\mathbf{x}_{k-1}-\hat{\mathbf{x}}_{k-1}\right)+\underbrace{\left.\frac{\partial \mathbf{f}_{k-1}}{\partial \mathbf{w}_{k-1}}\right|_{\hat{\mathbf{x}}_{k-1}, \mathbf{u}_{k-1}, \mathbf{0}}}_{\mathbf{L}_{k-1}} \mathbf{w}_{k-1}$

对于测量模型，线性化处理为：
$yk=hk(xk,vk)≈hk(xˇk,0)+∂hk∂xk∣xˇk,0⏟Hk(xk−xˇk)+∂hk∂vk∣xˇk,0⏟Mkvk\mathbf{y}_{k}=\mathbf{h}_{k}\left(\mathbf{x}_{k}, \mathbf{v}_{k}\right) \approx \mathbf{h}_{k}\left(\check{\mathbf{x}}_{k}, \mathbf{0}\right)+\underbrace{\left.\frac{\partial \mathbf{h}_{k}}{\partial \mathbf{x}_{k}}\right|_{\check{\mathbf{x}}_{k} ,\mathbf{0}}}_{\mathbf{H}_{k}} (\mathbf{x}_{k}-\check{\mathbf{x}}_{k})+\underbrace{\left.\frac{\partial \mathbf{h}_{k}}{\partial \mathbf{v}_{k}}\right|_{\check{\mathbf{x}}_{k} ,\mathbf{0}}}_{\mathbf{M}_{k}} \mathbf{v}_{k}$

在上面的方程中， $Fk−1,Lk−1,Hk,Mk\mathrm{F}_{k-1}, \mathrm{L}_{k-1}, \mathrm{H}_{k}, \mathrm{M}_{k}$ 被称为系统的雅可比矩阵。 正确计算这些雅可比矩阵是扩展卡尔曼滤波算法中最重要和最困难的步骤，也是最常见的出错地方。但是这些雅可比矩阵到底是什么？

3.3 Computing Jacobian Matrices

在上面的矩阵求导中，雅可比矩阵是一个包含所有一阶偏导数的矩阵。
$∂f∂x=[∂f∂x1⋯∂f∂xn]=[∂f1∂x1⋯∂f1∂xn⋮⋱⋮∂fm∂x1⋯∂fm∂xn]\frac{\partial \mathbf{f}}{\partial \mathbf{x}}=\left[ \begin{array}{ccc}{\frac{\partial \mathbf{f}}{\partial x_{1}}} & {\cdots} & {\frac{\partial \mathbf{f}}{\partial x_{n}}}\end{array}\right]=\left[ \begin{array}{ccc}{\frac{\partial f_{1}}{\partial x_{1}}} & {\cdots} & {\frac{\partial f_{1}}{\partial x_{n}}} \\ {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial f_{m}}{\partial x_{1}}} & {\cdots} & {\frac{\partial f_{m}}{\partial x_{n}}}\end{array}\right]$

直观上，雅可比矩阵告诉我们函数的每个输出沿每个输入维度的变化速度。 雅可比行列式实际上只是将一阶导数推广到多个维度。下面是带有两个输入的二维函数的雅可比矩阵简单示例。

$f(x)=[f1f2]=[x1+x2x12]→∂f∂x=[∂f1dx1∂f1∂x2∂f2dx1∂f2∂x2]=[112x10]\mathbf{f}(\mathbf{x})=\left[ \begin{array}{c}{f_{1}} \\ {f_{2}}\end{array}\right]=\left[ \begin{array}{c}{x_{1}+x_{2}} \\ {x_{1}^{2}}\end{array}\right] \quad \rightarrow \quad \frac{\partial \mathbf{f}}{\partial \mathbf{x}}=\left[ \begin{array}{cc}{\frac{\partial f_{1}}{d x_{1}}} & {\frac{\partial f_{1}}{\partial x_{2}}} \\ {\frac{\partial f_{2}}{d x_{1}}} & {\frac{\partial f_{2}}{\partial x_{2}}}\end{array}\right]=\left[ \begin{array}{cc}{1} & {1} \\ {2 x_{1}} & {0}\end{array}\right]$

现在，我们知道了如何计算EKF所需要的Jacobian矩阵，剩下的就是将它们代入我们的标准卡尔曼滤波器方程中，含有雅可比矩阵的扩展卡尔曼滤波器方程为：
在这里插入图片描述
最后，我们来看一个关于扩展卡尔曼滤波的简单示例：

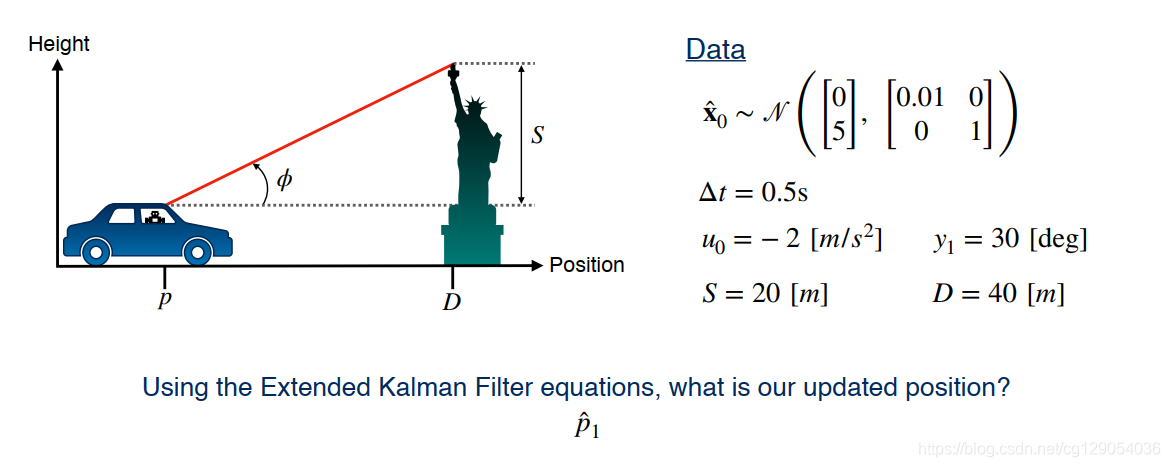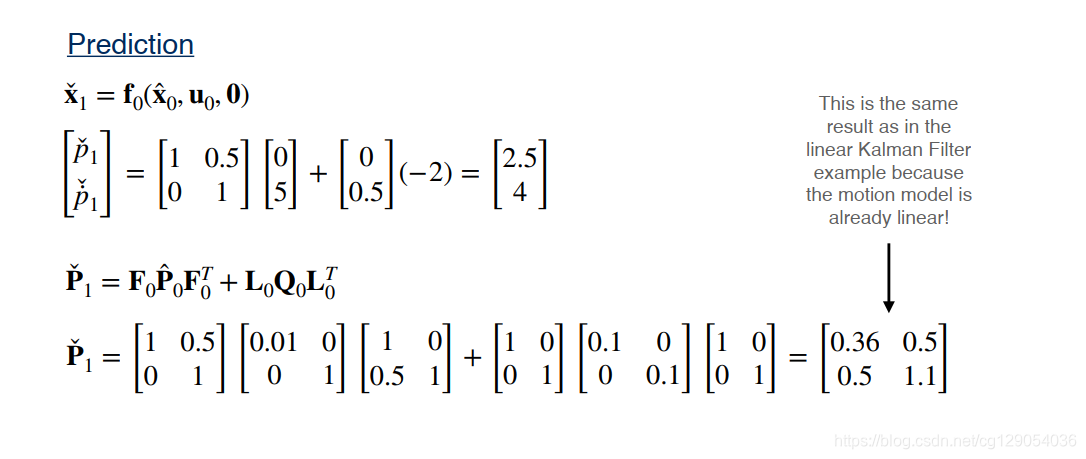4. Error State Kalman Filter

4.1 Overview

ES-EKF背后的思想非常简单。首先来看个简单的例子，如下图所示，该例子表示汽车位置的跟踪结果。 绿线为汽车的真实位置（称为真值状态），红线是估计位置（称为名义状态）。可以看到汽车位置真值状态 $x\mathbf{x}$ ，它由两部分组成：占据很大比重的为名义状态 $x^\hat\mathbf{x}$ ，而占据很小比重的称为误差状态 $δx\delta\mathbf{x}$ 。三者之间的关系为：
$x=x^+δx\mathbf{x} = \hat\mathbf{x} + \delta\mathbf{x}$
在这里插入图片描述
当然，我们的运动模型从来都不是完美的，并且总是存在一些随机的过程噪声。这些误差会随着时间不断累积，我们可以将误差状态视为所有这些模型误差和过程噪声随时间累积导致的，因此，误差状态就是在任何给定时间名义状态和真值状态之间的差异。如果我们能够弄清误差状态是什么，我们实际上可以将其作为对名义状态的修正，以使我们的预测更接近真值状态。

4.2 The Error-State Extended Kalman Filter

因此，在ES-EKF中，我们将使用EKF估计误差状态，然后使用误差状态估计值修正名义状态。在运动模型和测量模型中误差状态表示如下：
在这里插入图片描述

从上面的公式可以看出，ES-EKF与EKF的处理方法十分相似。

首先使用非线性运动模型和当前状态的最佳估计来更新名义状态。
$xˇk=fk−1(xk−1,uk−1,0)\begin{array}{c} \check{\mathbf{x}}_{k}=\mathbf{f}_{k-1}\left(\mathbf{x}_{k-1}, \mathbf{u}_{k-1}, \mathbf{0}\right) \end{array}$
然后是预测协方差矩阵。
$Pˇk=Fk−1Pk−1Fk−1T+Lk−1Qk−1Lk−1T\check{\mathbf{P}}_{k}=\mathbf{F}_{k-1} \mathbf{P}_{k-1} \mathbf{F}_{k-1}^{T}+\mathbf{L}_{k-1} \mathbf{Q}_{k-1} \mathbf{L}_{k-1}^{T}$
当有新的测量值到来时，首先计算卡尔曼增益：
$Kk=PˇkHkT(HkPˇkHkT+R)−1\mathbf{K}_{k}=\check{\mathbf{P}}_{k} \mathbf{H}_{k}^{T}\left(\mathbf{H}_{k} \check{\mathbf{P}}_{k} \mathbf{H}_{k}^{T}+\mathbf{R}\right)^{-1}$
然后是计算误差状态。
$δx^k=Kk(yk−hk(xˇk,0))\delta \hat{\mathbf{x}}_{k}=\mathbf{K}_{k}\left(\mathbf{y}_{k}-\mathbf{h}_{k}\left(\check{\mathbf{x}}_{k}, \mathbf{0}\right)\right)$
修正名义状态。
$x^=xˇ+δx^\hat\mathbf{x}=\check\mathbf{x} + \delta\hat\mathbf{x}$
最后更新协方差矩阵。
$P^k=(I−KkHk)Pˇk\hat{\mathbf{P}}_{k} =\left(\mathbf{I}-\mathbf{K}_{k} \mathbf{H}_{k}\right) \check\mathbf{P}_{k}$

4.3 Why Use the ES-EKF?

使用ES-EKF的主要原因有两个：

一是误差状态相比EKF中的名义状态可以更好地用在线性滤波中。
另一个原因是当状态量中有旋转变量时，使用误差状态可以很方便地计算，我们可以将真值状态拆解为两种状态分别来计算，即：
$x=x^⊕δx\mathbf{x}=\hat{\mathbf{x}} \oplus \delta \mathbf{x}$

5. Limitations of the EKF

5.1 Linearization error

从前面几小节中，我们已经知道EKF或ES-EKF 通过线性化非线性运动模型和测量模型来更新状态估计的均值和协方差。线性化模型只是非线性模型的局部线性近似。通常将线性近似模型与真实模型之间的差称为线性化误差。一般来说，任何非线性函数的线性化误差取决于：

首先是原始函数的非线性程度。如果非线性函数 $f (x)$ 变化非常缓慢，线性近似将是一个很好的拟合。如果函数变化很快，线性近似就不能很好地捕捉函数在其大部分域中的真实形状。
第二点是与近似点之间的距离。从下图可以看出，离近似点 $a$ 越远，线性化误差就越大。

在这里插入图片描述

5.2 Example

现在让我们看一个例子，如下图所示为从极坐标 $r$ 和 $θ\theta$ 到笛卡尔坐标 $x$ 和 $y$ 的非线性变换和线性变换。其实这种变换通常用于自动驾驶汽车LiDAR传感器数据的处理。
在这里插入图片描述
左边极坐标中蓝点为均匀分布。当我们将这些样本中的每一个点转换为相应的笛卡尔坐标时，我们看到变换分布呈现香蕉形状，如右图所示。显然，仅使用均值和协方差并不能完全捕获香蕉分布的形状。

在左图中，均匀分布的样本均值显示为中间的绿点，真实协方差由绿色椭圆表示。让我们比较线性化和非线性化变换分布。可以看到线性化分布的均值与真实均值相差很大，线性化协方差严重低估了真实输出分布沿 $y$ 轴维度的分布。

5.3 Limitations of the EKF

现在让我们总结一下EKF的使用限制：

容易产生线性化误差，特别时当系统运动模型和测量模型高度非线性时；或当传感器采样时间过慢时（与自动驾驶汽车速度相比），也会产生很大的线性化误差。
线性化误差很大时，会产生两个结果：一是估计值可能与真实值相差很大，二是估计协方差可能无法准确捕捉状态的真实不确定性，这会导致整个系统发散，而且通常很难再收敛回来。
在实践中最常见的问题是在计算雅可比矩阵时很容易出错，尤其是在处理复杂的非线性系统时。工程上也有人试图通过使用数值微分或在编译时使用自动微分来解决这个问题。但是这些都有自己的陷阱，有时会表现得不可预测。

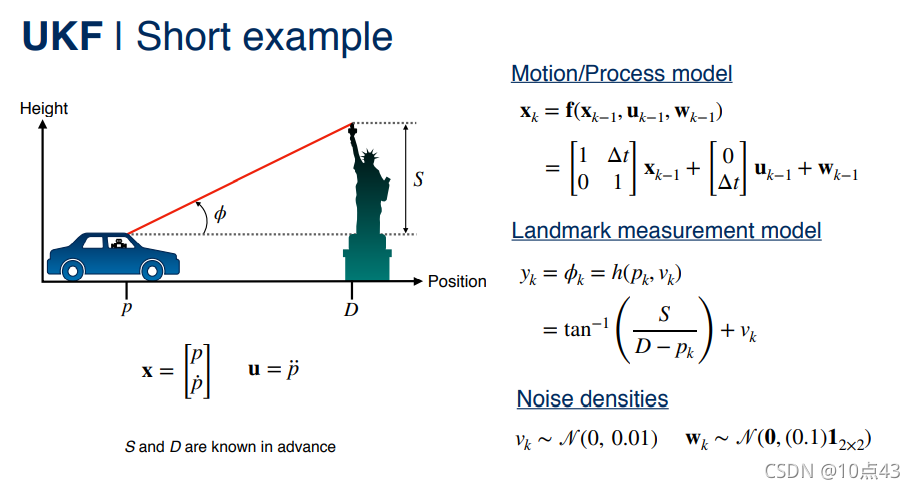
6. Unscented Kalman Filter

6.1 The Unscented Transform

在本小节，我们将学习非线性滤波的另一种方法，无损卡尔曼滤波。无损变换的背后思想是：近似概率分布比近似任意非线性函数更容易。让我们来看下面一张图，其中左侧的一维高斯分布通过非线性函数 $y = h (x)$ 转换为更复杂的一维分布。

在这里插入图片描述
我们已经知道输入变量 $x$ 的均值和标准差，我们想使用这些信息和非线性函数计算输出 $y$ 的均值和标准差。无损变换为我们提供了一种方法来做到这一点。无损变换的基本思想分为三个步骤。

首先，我们从输入分布中选择一组样本点。这些不是随机样本，它们是确定性样本，它们被选择为远离平均值一定数量的标准差。出于这个原因，这些样本被称为 sigma points。
一旦我们有了精心选择的sigma points，第二个也是最简单的步骤是将每个 sigma point 通过我们的非线性函数，产生一组属于输出分布的新sigma point。
最后，我们可以使用一些精心选择的权重来计算输出 sigma points的样本均值和协方差，这将使我们能够很好地近似真实输出分布的均值和协方差。

现在我们已经了解了无损变换的思想，下面让我们看看如何选取 sigma point以及如何计算新的分布均值和协方差。

(1) 选取sigma point

通常，对于 $n$ 维概率分布，我们需要 $2 n + 1$ 个 sigma point，一个为均值，其余关于均值对称分布。下图显示了一维和二维示例的sigma point。在一维中我们需要三个sigma point，而在二维中我们需要五个sigma point。

选取 sigma point 的第一步是对输入分布的协方差矩阵进行 Cholesky分解。计算 Cholesky分解，可以使用 MATLAB 中的 chole 函数或 NumPy 中的 Cholesky 函数。

一旦完成协方差矩阵分解，我们就可以选择分布均值作为第一个 sigma point，其余 sigma point 的选择可以用图中的公式来实现。其中 $κ\kappa$ 参数一般取值为3， $N$ 为维度。

$xi=μx+N+κcol⁡iLi=1,…,Nxi+N=μx−N+κcol⁡iLi=1,…,N\mathbf{x}_{i}=\boldsymbol{\mu}_{x}+\sqrt{N+\kappa} \operatorname{col}_{i} \mathbf{L} \quad i=1, \ldots, N \\ \mathbf{x}_{i+N}=\boldsymbol{\mu}_{x}-\sqrt{N+\kappa} \operatorname{col}_{i} \mathbf{L} \quad i=1, \ldots, N$
在这里插入图片描述
(2) 计算均值和协方差
现在我们有了一组 sigma poionts。下一步很简单，只需通过我们的非线性函数 $h (x)$ 传递每个 sigma point 即可获得一组新的转换后的 sigma points，即：
$yi=h(xi)i=0,…,2N\mathbf{y}_{i}=\mathbf{h}\left(\mathbf{x}_{i}\right) \quad i=0, \ldots, 2 N$
均值和协方差计算公式为：
$μy=∑i=02NαiyiΣyy=∑i=02Nαi(yi−μy)(yi−μy)T\boldsymbol{\mu}_{y}=\sum_{i=0}^{2 N} \alpha_{i} \mathbf{y}_{i} \\ {\Sigma}_{y y}=\sum_{i=0}^{2 N} \alpha_{i}\left(\mathbf{y}_{i}-\boldsymbol{\mu}_{y}\right)\left(\mathbf{y}_{i}-\boldsymbol{\mu}_{y}\right)^{T}$

其中，权重 $αi\alpha_i$ 的计算公式为：
$\alpha_{i}=\left\{\begin{array}{ll} \frac{\kappa}{N+\kappa} & i=0 \\ \frac{1}{2} \frac{1}{N+\kappa} & \text { otherwise } \end{array}\right.$

现在我们看看使用无损变换后极坐标到直角坐标变换的结果，如下图所示。我们输入分布的维度是 $2$ ，所以我们需要 $5$ 个 sigma point，我们用橙色星星表示。从右图可以看出，我们使用无损变换对均值的估计与真正的非线性均值几乎完全相同，并且我们对协方差的估计也几乎与真正的协方差相匹配。可以看出，无损变换比线性化变换得到的结果要好许多。
在这里插入图片描述

6.2 Unscented Kalman Filter (UKF)

现在我们已经掌握了无损变换的工作原理，我们可以在卡尔曼滤波框架中轻松使用它来处理非线性模型，这时我们称其为无损卡尔曼滤波或 UKF。记住其主要思想是：我们不是像 EKF 那样通过线性化来逼近系统方程，而是使用无损变换来直接逼近 PDF。

(1) Prediction
我们先来看预测步骤，主要分为三步：

选取 sigma points。
$L^k−1L^k−1T=P^k−1x^k−1(0)=x^k−1x^k−1(i)=x^k−1+N+κcol⁡iL^k−1i=1…Nx^k−1(i+N)=x^k−1−N+κcol⁡iL^k−1i=1…N\begin{aligned} \hat{\mathbf{L}}_{k-1} \hat{\mathbf{L}}_{k-1}^{T} &=\hat{\mathbf{P}}_{k-1} \\ \hat{\mathbf{x}}_{k-1}^{(0)} &=\hat{\mathbf{x}}_{k-1} \\ \hat{\mathbf{x}}_{k-1}^{(i)} &=\hat{\mathbf{x}}_{k-1}+\sqrt{N+\kappa} \operatorname{col}_{i} \hat{\mathbf{L}}_{k-1} \quad i=1 \ldots N \\ \hat{\mathbf{x}}_{k-1}^{(i+N)} &=\hat{\mathbf{x}}_{k-1}-\sqrt{N+\kappa} \operatorname{col}_{i} \hat{\mathbf{L}}_{k-1} \quad i=1 \ldots N \end{aligned}$
非线性变换 sigma points。
$xˇk(i)=fk−1(x^k−1(i),uk−1,0)i=0…2N\check{\mathbf{x}}_{k}^{(i)}=\mathbf{f}_{k-1}\left(\hat{\mathbf{x}}_{k-1}^{(i)}, \mathbf{u}_{k-1}, \mathbf{0}\right) \quad i=0 \ldots 2 N$
计算新的均值的协方差。
$xˇk=∑i=02Nα(i)x˙k(i)Pˇk=∑i=02Nα(i)(xˇk(i)−xˇk)(xˇk(i)−xˇk)T+Qk−1\begin{aligned} &\alpha^{(i)}= \begin{cases}\frac{\kappa}{N+\kappa} & i=0 \\ \frac{1}{2} \frac{1}{N+\kappa} & \text { otherwise }\end{cases} \\ &\check{\mathbf{x}}_{k}=\sum_{i=0}^{2 N} \alpha^{(i)} \dot{\mathbf{x}}_{k}^{(i)} \\ &\check{\mathbf{P}}_{k}=\sum_{i=0}^{2 N} \alpha^{(i)}\left(\check{\mathbf{x}}_{k}^{(i)}-\check{\mathbf{x}}_{k}\right)\left(\check{\mathbf{x}}_{k}^{(i)}-\check{\mathbf{x}}_{k}\right)^{T}+\mathbf{Q}_{k-1} \end{aligned}$

(2) Correction
修正分为四步。

从 sigma points 计算预测测量。
$y^k(i)=hk(xˇk(i),0)i=0,…,2N\hat{\mathbf{y}}_{k}^{(i)}=\mathbf{h}_{k}\left(\check{\mathbf{x}}_{k}^{(i)}, \mathbf{0}\right) \quad i=0, \ldots, 2 N$
计算预测测量均值和协方差。
$y^k=∑i=02Nα(i)y^k(i)Py=∑i=02Nα(i)(y^k(i)−y^k)(y^k(i)−y^k)T+Rk\begin{aligned} \hat{\mathbf{y}}_{k} &=\sum_{i=0}^{2 N} \alpha^{(i)} \hat{\mathbf{y}}_{k}^{(i)} \\ \mathbf{P}_{y} &=\sum_{i=0}^{2 N} \alpha^{(i)}\left(\hat{\mathbf{y}}_{k}^{(i)}-\hat{\mathbf{y}}_{k}\right)\left(\hat{\mathbf{y}}_{k}^{(i)}-\hat{\mathbf{y}}_{k}\right)^{T}+\mathbf{R}_{k} \end{aligned}$
计算卡尔曼增益。
$Pxy=∑i=02Nα(i)(xˇk(i)−xˇk)(y^k(i)−y^k)TKk=PxyPy−1\begin{aligned} \mathbf{P}_{x y} &=\sum_{i=0}^{2 N} \alpha^{(i)}\left(\check{\mathbf{x}}_{k}^{(i)}-\check{\mathbf{x}}_{k}\right)\left(\hat{\mathbf{y}}_{k}^{(i)}-\hat{\mathbf{y}}_{k}\right)^{T} \\ \mathbf{K}_{k} &=\mathbf{P}_{x y} \mathbf{P}_{y}^{-1} \end{aligned}$
计算修正后的均值和协方差。
$x^k=xˇk+Kk(yk−y^k)P^k=Pˇk−KkPyKkT\begin{aligned} \hat{\mathbf{x}}_{k} &=\check{\mathbf{x}}_{k}+\mathbf{K}_{k}\left(\mathbf{y}_{k}-\hat{\mathbf{y}}_{k}\right) \\ \hat{\mathbf{P}}_{k} &=\check{\mathbf{P}}_{k}-\mathbf{K}_{k} \mathbf{P}_{y} \mathbf{K}_{k}^{T} \end{aligned}$

现在我们再重新看看本讲开始的汽车一维位置估计的例子。

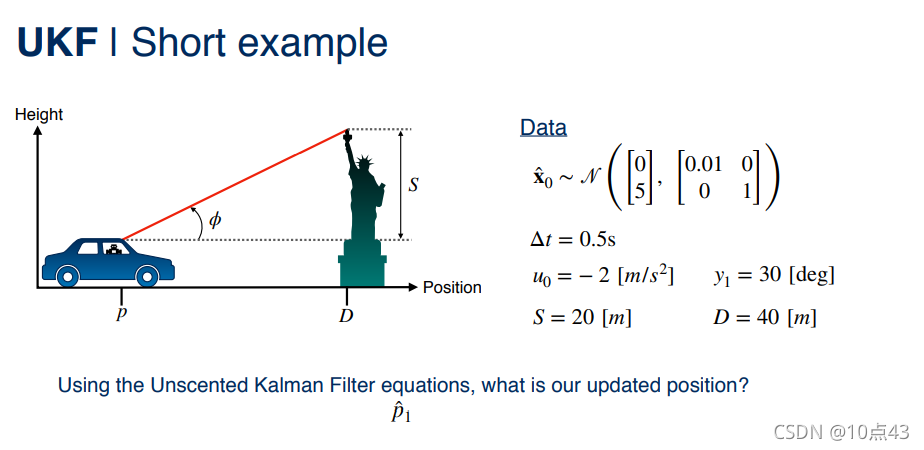7. Summary

简单总结一下：

本讲我们首先讨论了线性卡尔曼滤波器，它是一种递归最小二乘估计形式，允许我们将来自运动模型的信息与来自传感器测量的信息相结合，以估计车辆状态。卡尔曼滤波器遵循预测-修正架构。运动模型用于对状态进行预测，测量值用于对这些预测进行校正。
我们还看到卡尔曼滤波器是最好的线性无偏估计器，即 BLUE。也就是说，卡尔曼滤波器是最好的无偏估计器，它仅使用测量的线性组合。但是，当然线性系统在现实中并不真正存在，因此我们需要开发处理非线性系统的技术。
我们研究了三种不同的非线性卡尔曼滤波方法：扩展卡尔曼滤波器（EKF）、误差状态卡尔曼滤波器（ES-EKF）和无损卡尔曼滤波器或（UKF）。正如我们所讨论的，主要区别在于 EKF 依靠局部分析线性化来通过非线性函数传播 PDF，无论是EKF 还是 ES-EKF。相比之下，UKF 依靠无损变换来处理非线性函数。三者对比如下表示所示。