UML用例图

统一建模语言（Unified Modeling Language，UML）又称标准建模语言，是始于1997年的一个OMG标准，它是一个支持模型化和软件系统开发的图形化语言，为软件开发的所有阶段提供模型化和可视化支持，包括由需求分析到规格，到构造和配置。

　　*注：OMG, Object Management Group 对象管理组织

2.UML常见图分类

　　UML从考虑系统的不同角度出发，定义了用例图、类图、对象图、包图、状态图、活动图、序列图、协作图、构件图、部署图等10种图。

　　常见的UML图有用例图（Use Case Diagram）、类图（Class Diagram）和序列图（Sequence Diagram）。下面也将主要阐述这三种UML图.

 

3.用例图

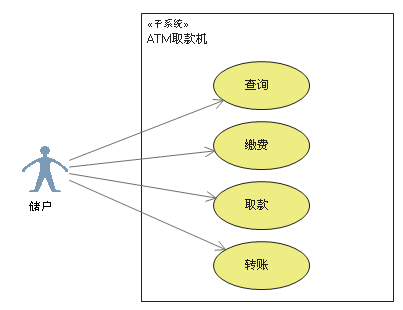
　　用例图，展现了一组用例、参与者（actor）以及它们之间的关系。用例图从用户角度描述系统的静态使用情况，用于建立需求模型。

 

参与者（Actor）

　　在系统外部与系统直接交互的人或事物。需要注意以下两点：

　　1）参与者是角色而不是具体的人，它代表了参与者在与系统打交道的过程中所扮演的角色。所以在系统的实际运作中，一

个实际用户可能对应系统的多个参与者。不同的用户也可以只对应于一个参与者，从而代表同一参与者的不同实例。

　　2）参与者作为外部用户（而不是内部）与系统发生交互作用，是它的主要特征。

　　在UML中，参与者使用如图所示的一个小人表示：

 

用例（Use Case）

　　系统外部可见的一个系统功能单元。系统的功能由系统单元所提供，并通过一系列系统单元与一个或多个参与者之间交换的消息所表达。用椭圆表示，椭圆中的文字简述系统的功能：

子系统(Subsystem)

　　用来展示系统的一部分功能，这部分功能联系紧密。

 

 

关系（Relationship）

　　常见关系类型有关联、泛化、包含和扩展。

　　以上各关系在uml图中的表示方式，如下表所示：

　　

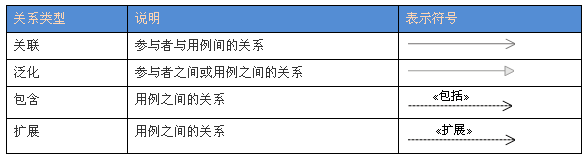
　　a. 关联(Association)

　　表示参与者与用例之间的通信，任何一方都可发送或接受消息。

　　【箭头指向】：指向消息接收方

　　b. 泛化(Inheritance)

　　就是通常理解的继承关系，子用例和父用例相似，但表现出更特别的行为；子用例将继承父用例的所有结构、行为和关系。子用例可以使用父用例的一段行为，也可以重载它。父用例通常是抽象的。

　　【箭头指向】：指向父用例

　　c. 包含(Include)

　　包含关系用来把一个较复杂用例所表示的功能分解成较小的步骤。

　　【箭头指向】：指向分解出来的功能用例

　　d. 扩展(Extend)

　　扩展关系是指用例功能的延伸，相当于为基础用例提供一个附加功能。

　　【箭头指向】：指向基础用例

　

 

包含(include)、扩展(extend)、泛化(Inheritance) 的区别：

　　条件性：泛化中的子用例和include中的被包含的用例会无条件发生，而extend中的延伸用例的发生是有条件的；

　　直接性：泛化中的子用例和extend中的延伸用例为参与者提供直接服务，而include中被包含的用例为参与者提供间接服务。

　　对extend而言，延伸用例并不包含基础用例的内容，基础用例也不包含延伸用例的内容。

　　对Inheritance而言，子用例包含基础用例的所有内容及其和其他用例或参与者之间的关系；