说明:本文是七月算法5月深度学习班第一次课听课笔记。只记录关键知识点,有些没具体展开。帮助复习用。文中使用了老师课件中的公式。
微积分
导数
定义常用函数导数导数法则
加法 乘法 除法 链式法则
一元函数与多元函数
一阶导 一元函数 f'(x)多元函数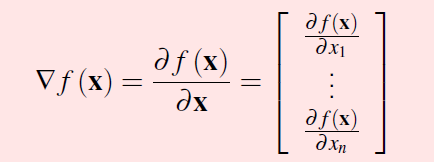
二阶导 一元函数f‘’(x)多元函数Hessian矩阵
泰勒级数
泰勒级数公式 一元版和多元版
一级导数=0 这一点可能为 平稳点、极值点、鞍点。如果二级导数>0,是极小值点;二级导数<0,是极大值点。二级导数=0,是鞍点。注意在多元函数中二级导数>0,就是指hession矩阵>0(正定矩阵)。
梯度下降
为了找到函数最小值,首先要求一阶导数。当原函数的导数不好求,或者不可求的时候选择梯度下降。为什么是梯度下降?在函数已知点 (xk,f(xk)) ,走一个方向 delta。怎么才能让函数最快上升呢?根据上面的泰勒级数公式,当 delta = 梯度方向的时候,可以取到最大值,所以函数增长会最大。
当需要求函数最小值的时候,只要沿着负梯度方向就可以了。当然这里还有一个重要的参数是步长。
概率论
随机变量
离散型 分布式函数连续型 累计分布函数概率密度函数
高斯分布
表达式 一元版 多元函数版中心极限定理多个(>=4)泊松分布的和是高斯分布独立高斯变量相加=高斯分布
贝叶斯公式
贝叶斯公式用于推断一件事情发生的可能性。
通过 公式1和公式2推出公式3,进而得到公式4,贝叶斯公式。P(A|B)是后验概率,P(B)是一个确定的事件,P(A)是先验概率,P(B|A)是似然函数。
吸毒案例学习注意:当先验概率很低的时候,即使似然函数有很高的值,结果也可能很低。
矩阵
特征向量与特征值
A为一个矩阵 ,X为一个向量,r为一个实数。如果 AX=rX。则X是A的特征向量,r是特征值。也就是说一个向量,经过矩阵A的变换之后,仍然和原向量共线。矩阵所有特征值不同=> 特征向量线性无关
对称矩阵特征分解
PCA
对象 操作 结果X 协方差 = CxCx SVD = U(单位特征向量)(U转置) X 内积 = Y 对(X做去相关操作)Y 协方差 = Cy 对角阵,对角元素是X的特征值,按照从小到大排序与U中的列 特征向量正好 对应,形成特征向量与特征值
U[:,:k] X 内积 = 降维后的矩阵
凸优化
一般有约束的优化问题
KKT条件
将约束转为无约束
凸优化问题
无约束问题求解--------SGD有约束优化问题 --------------拉格朗日乘子--------无约束问题-----------KKT 求解
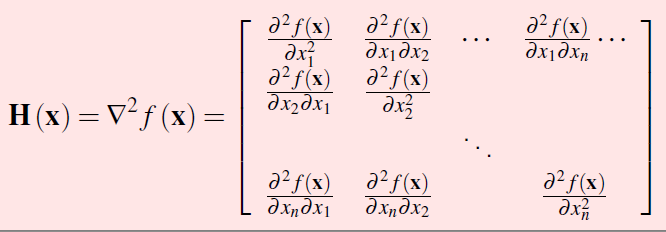
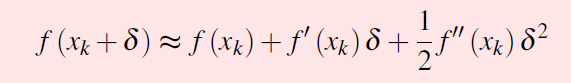
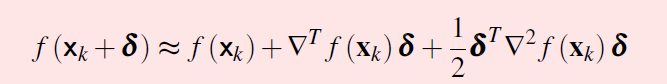
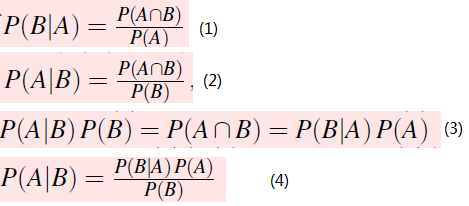


![[Leetcode][第1025题][JAVA][除数博弈][数学][递推]](http://pic.xiahunao.cn/[Leetcode][第1025题][JAVA][除数博弈][数学][递推])

![[Leetcode][第410题][JAVA][分割数组的最大值][动态规划][二分]](http://pic.xiahunao.cn/[Leetcode][第410题][JAVA][分割数组的最大值][动态规划][二分])



![[小技巧][Java]Arrays.fill() 初始化 二维数组](http://pic.xiahunao.cn/[小技巧][Java]Arrays.fill() 初始化 二维数组)



![[算法][算法复杂度]常用算法复杂度速查表](http://pic.xiahunao.cn/[算法][算法复杂度]常用算法复杂度速查表)


![[Leetcode][第329题][JAVA][矩阵中的最长递增路径][DFS][拓扑排序]](http://pic.xiahunao.cn/[Leetcode][第329题][JAVA][矩阵中的最长递增路径][DFS][拓扑排序])


![[小技巧][JAVA][转换]字符数组char[]与字符串String之间互相转换](http://pic.xiahunao.cn/[小技巧][JAVA][转换]字符数组char[]与字符串String之间互相转换)
)