【问题描述】[中等]

【解答思路】

1. 动态规划

第 1 步：设计状态
令 f[i][j] 表示将数组的前 i 个数分割为 j 段所能得到的最大连续子数组和的最小值。 （ i ≥ j ）
第 2 步：状态转移方程

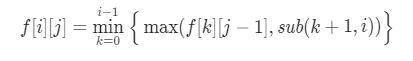
第 3 步：考虑初始化
f[i][j] = Integer.MAX_VALUE
f[0][0]=0
第 4 步：考虑输出
f[n][m]f[n][m]

复杂度

class Solution {public int splitArray(int[] nums, int m) {int n = nums.length;int[][] f = new int[n + 1][m + 1];for (int i = 0; i <= n; i++) {Arrays.fill(f[i], Integer.MAX_VALUE);}int[] sub = new int[n + 1];for (int i = 0; i < n; i++) {sub[i + 1] = sub[i] + nums[i];}f[0][0] = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= Math.min(i, m); j++) {for (int k = 0; k < i; k++) {f[i][j] = Math.min(f[i][j], Math.max(f[k][j - 1], sub[i] - sub[k]));}}}return f[n][m];}
}

2. 二分+贪心

nums = [7,2,5,10,8]
m = 1，那么整个数组作为一部分，最小的最大值为 32
m = n，那么每个元素作为一个子数组，从所有元素选取最大值，最小的最大值小为 10
m 的取值范围为 1 <= m <= n，因此，最大值的最小值的范围为 [10, 32]
我们利用二分法查找，找出符合 m 的最大值的最小的结果
二分过程：
left = 10;
right = 32
mid = (left + right) >>> 1 = 21（这个 21 就是一个子数组的最大容量）
我们假设刚开辟的用来存储的子数组个数 cnt = 1
那么根据贪心思想，我们将数组元素按顺序逐个往里放
因此就有如下过程：
7 < 21
7 + 2 < 21
7 + 2 + 5 < 21
7 + 2 + 5 + 10 > 21
至此，我们可以看出一个 21 容量的子数组是无法容纳整个数组元素的，因此我们需要开辟第二个子数组来存储剩下的数组元素
cnt = cnt + 1 = 2
10 < 21
10 + 8 < 21
我们发现，两个子数组可以将整个数组元素放入，而 cnt 刚好等于 m，因此 [7,2,5] 和 [10,8] 就是分割出来的两个子数组，最小的最大值为 18

区间缩小 （建议在草稿纸上模拟过程）

1. [10.31]
2. [10.21]
3. [16,21]
4. [16,18]
5. [17.18]
6. [18.18]

为什么是放入元素直到放不下为止？因为要求的是连续子数组，我们需要保证每个连续的子数组的元素和都尽可能的接近 21

如果我们最终得到的 cnt > m，那么表示我们划分出太多的子数组，也就是意味着一个子数组的容量太少，我们需要再扩大容量，即 left = mid + 1，然后继续进行二分
如果我们最终得到的 cnt < m，那么表示我们划分出太少的子数组，也就是意味着一个子数组的容量太大，需要减少容量，即 right = mid
复杂度

public class Solution {public int splitArray(int[] nums, int m) {int max = 0;int sum = 0;// 计算「子数组各自的和的最大值」的上下界for (int num : nums) {max = Math.max(max, num);sum += num;}// 使用「二分查找」确定一个恰当的「子数组各自的和的最大值」，// 使得它对应的「子数组的分割数」恰好等于 mint left = max;int right = sum;while (left < right) {int mid = left + (right - left) / 2;int splits = split(nums, mid);if (splits > m) {// 如果分割数太多，说明「子数组各自的和的最大值」太小，此时需要将「子数组各自的和的最大值」调大// 下一轮搜索的区间是 [mid + 1, right]left = mid + 1;} else {// 下一轮搜索的区间是上一轮的反面区间 [left, mid]right = mid;}}return left;}/***** @param nums 原始数组* @param maxIntervalSum 子数组各自的和的最大值* @return 满足不超过「子数组各自的和的最大值」的分割数*/private int split(int[] nums, int maxIntervalSum) {// 至少是一个分割int splits = 1;// 当前区间的和int curIntervalSum = 0;for (int num : nums) {// 尝试加上当前遍历的这个数，如果加上去超过了「子数组各自的和的最大值」，就不加这个数，另起炉灶if (curIntervalSum + num > maxIntervalSum) {curIntervalSum = 0;splits++;}curIntervalSum += num;}return splits;}public static void main(String[] args) {int[] nums = new int[]{7, 2, 5, 10, 8};int m = 2;Solution solution = new Solution();int res = solution.splitArray(nums, m);System.out.println(res);}
}

【总结】

1. 动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2.细节

Arrays.fill()并不能提高赋值的效率，在函数的内部也是用for循环的方式 实现的。
fill()函数源码：

    public static void fill(Object[] a, Object val) {for (int i = 0, len = a.length; i < len; i++)a[i] = val;}

 for (int i = 0; i <= n; i++) {Arrays.fill(f[i], Integer.MAX_VALUE);}

等价于

for (int i = 0; i <= n; i++) {for(int j =0 ;j<=m;j++){f[i][j] = Integer.MAX_VALUE;}}

3.审题认真！ Java函数不懂可以看源码， 效率超高！（总比瞎猜好）

参考链接：https://leetcode-cn.com/problems/split-array-largest-sum/solution/er-fen-cha-zhao-by-liweiwei1419-4/
参考链接：https://leetcode-cn.com/problems/split-array-largest-sum/solution/fen-ge-shu-zu-de-zui-da-zhi-by-leetcode-solution/