梯度下降
损失函数可视化
得分函数 f=W*X
损失函数 c=W*X-y
目标 损失函数最小 最优化过程
可视化
一维
二维 热力图
如果损失函数是一个凸函数,例如SVM。
凸函数 正系数加和=凸函数
神经网络 costfunction 非凸 因为系数有正有负。
凸优化与最优化
神经网络最优化方法是梯度下降。梯度下降策略有:1 随机搜索。随机生成一组权重,与之前的loss相比,小了,就是更更好的权重。
2 随机局部搜索。在现有权重的周围随机生成一组权重。选择最优权重。
3 顺着梯度下滑。梯度方向是函数增长最快的方向。随意顺梯度下降,就是最快能到达最小值的方式。梯度下降是初始值敏感的,不同的初始值可能到达的最小值点不同。一般使用高斯分布的随机小值。
梯度下降
梯度下降有两种解决。数值梯度和解析梯度。数值梯度是按照导数公式 f(x0)' = (f(x0+h) - f(x0))/h ,h是一个非常小的数。数值梯度解法简单,但是计算和参数呈线性关系,计算量大。解析法:速度快,但是容易出错。利用f(x)导函数 f(x)' 计算梯度。
梯度下降的实现过程中有批处理、随机梯度、min-batch梯度下降。
梯度下降要理解梯度方向需要弄明白 梯度方向 三垂线 几个概念。我记录一点杂乱的东西在这里。梯度:函数增长最快的方向。梯度方向是等值曲线的法向量。是函数在某一点的变化率和变化方向。在一维函数的时候,梯度方向和
反向传播
反向转播是一个求偏导的过程。
链式法则
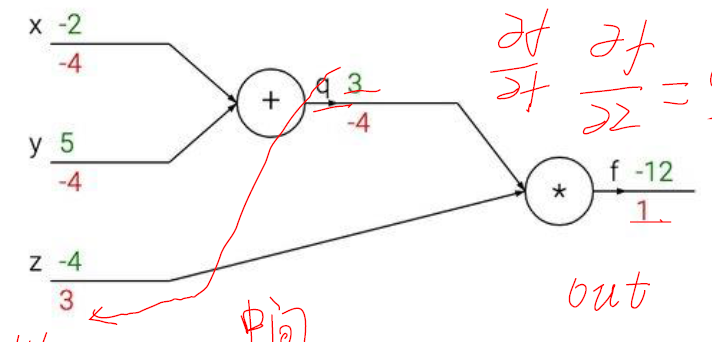
把 f(x,y,z)=(x+y)*z 在给定一个具体值的时候画一个网络结构图试试吧。前向计算每一步的得分。向后计算每一步的导数。
Sigmoid例子和公式推导
这个公式推导真心没推导出来。继续加油。



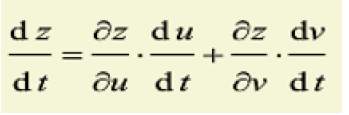
![[Leetcode][第1025题][JAVA][除数博弈][数学][递推]](http://pic.xiahunao.cn/[Leetcode][第1025题][JAVA][除数博弈][数学][递推])

![[Leetcode][第410题][JAVA][分割数组的最大值][动态规划][二分]](http://pic.xiahunao.cn/[Leetcode][第410题][JAVA][分割数组的最大值][动态规划][二分])



![[小技巧][Java]Arrays.fill() 初始化 二维数组](http://pic.xiahunao.cn/[小技巧][Java]Arrays.fill() 初始化 二维数组)



![[算法][算法复杂度]常用算法复杂度速查表](http://pic.xiahunao.cn/[算法][算法复杂度]常用算法复杂度速查表)


![[Leetcode][第329题][JAVA][矩阵中的最长递增路径][DFS][拓扑排序]](http://pic.xiahunao.cn/[Leetcode][第329题][JAVA][矩阵中的最长递增路径][DFS][拓扑排序])


![[小技巧][JAVA][转换]字符数组char[]与字符串String之间互相转换](http://pic.xiahunao.cn/[小技巧][JAVA][转换]字符数组char[]与字符串String之间互相转换)
)

![[小技巧][JAVA][转换]整型int与字符串String相互转换](http://pic.xiahunao.cn/[小技巧][JAVA][转换]整型int与字符串String相互转换)