[剑指offer]面试题第[41]题[Leetcode][第235题][JAVA][数据流中的中位数][优先队列][堆]

【问题描述】[困难]

在这里插入图片描述

【解答思路】

1. 思路1

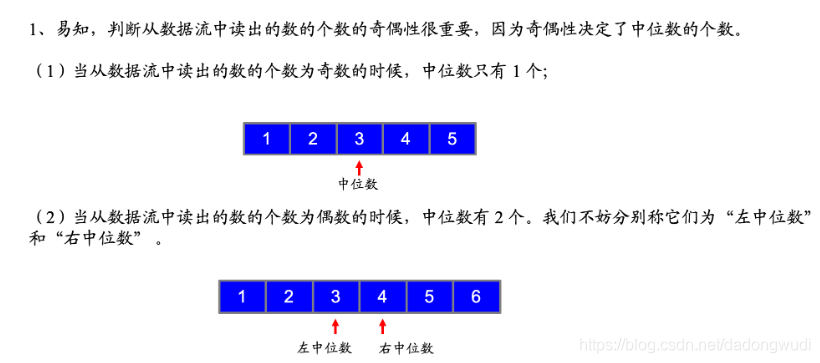
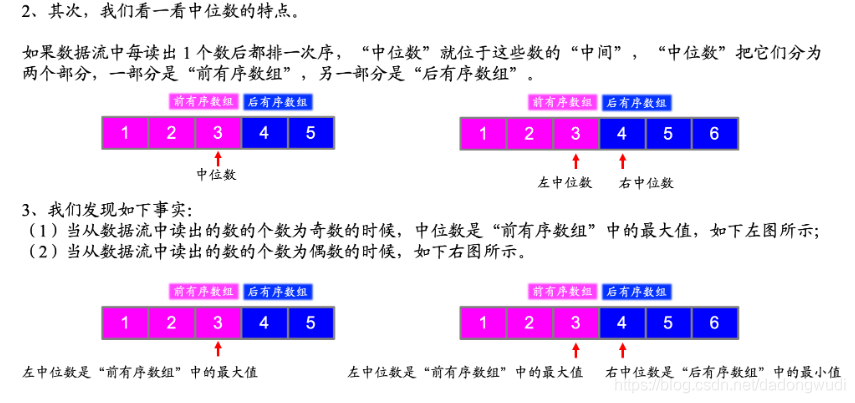
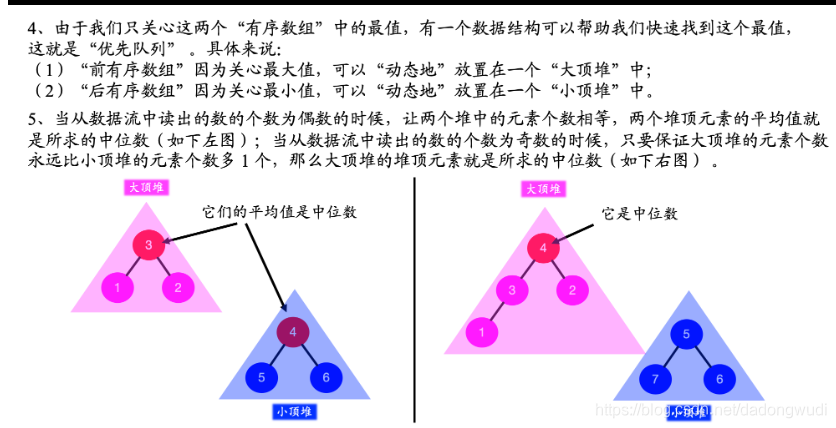
在这里插入图片描述

时间复杂度：O(logN) 空间复杂度：O(N)

import java.util.PriorityQueue;public class MedianFinder {/*** 当前大顶堆和小顶堆的元素个数之和*/private int count;private PriorityQueue<Integer> maxheap;private PriorityQueue<Integer> minheap;/*** initialize your data structure here.*/public MedianFinder() {count = 0;//maxHeap = new PriorityQueue<>(Collections.reverseOrder());maxheap = new PriorityQueue<>((x, y) -> y - x);minheap = new PriorityQueue<>();}public void addNum(int num) {count += 1;maxheap.offer(num);minheap.add(maxheap.poll());// 如果两个堆合起来的元素个数是奇数，小顶堆要拿出堆顶元素给大顶堆if ((count & 1) != 0) {maxheap.add(minheap.poll());}/*//如果不平衡则调整 不用countif (minHeap.size() > maxHeap.size()) {maxHeap.offer(minHeap.poll());}*/}public double findMedian() {if ((count & 1) == 0) {// 如果两个堆合起来的元素个数是偶数，数据流的中位数就是各自堆顶元素的平均值return (double) (maxheap.peek() + minheap.peek()) / 2;} else {// 如果两个堆合起来的元素个数是奇数，数据流的中位数大顶堆的堆顶元素return (double) maxheap.peek();}
//不用count
public double findMedian() {if (maxHeap.size() == minHeap.size()) {return (maxHeap.peek() + minHeap.peek()) * 0.5;}return maxHeap.peek();}}
}

2. 思路2

在这里插入图片描述

复杂度
在这里插入图片描述

class MedianFinder {Queue<Integer> A, B;public MedianFinder() {A = new PriorityQueue<>(); // 小顶堆，保存较大的一半B = new PriorityQueue<>((x, y) -> (y - x)); // 大顶堆，保存较小的一半}public void addNum(int num) {if(A.size() != B.size()) {A.add(num);B.add(A.poll());} else {B.add(num);A.add(B.poll());}}public double findMedian() {return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;}
}

【总结】

1.最大堆/最小堆初始化

最小堆
PriorityQueue minheap = new PriorityQueue<>();
最大堆
PriorityQueue maxheap = new PriorityQueue<>((x, y) -> y - x);
PriorityQueue maxHeap = new PriorityQueue<>(Collections.reverseOrder());