by Aloïs Bissuel, Vincent Grosbois and Benjamin Heymann

AloïsBissuel，Vincent Grosbois和Benjamin Heymann撰写

The recent media debate on COVID-19 drugs is a unique occasion to discuss why decision making in an uncertain environment is a complicated but fundamental topic in our technology-based, data-fueled societies.

最近有关COVID-19药物的媒体辩论是讨论我们为何在以技术为基础，以数据为动力的社会中为什么在不确定的环境中进行决策是一个复杂而基本的话题的难得的机会。

Aside from systematic biases — which are also an important topic —any scientific experiment is subject to a lot of unfathomable, noisy, or random phenomena.For example when one wants to know the effect of a drug on a group of patients, one may always wonder “If I were to take a similar group to renew the test, would I get the same result?” Such an experiment would at best end up with similar results. Hence the right question is probably something like “Would my conclusions still hold?” Several dangers await the uncautious decision-maker.

除了系统性偏见(这也是一个重要的话题)之外，任何科学实验都受到许多难以理解，嘈杂或随机现象的影响。例如，当一个人想知道某种药物对一组患者的作用时，可能总是纳闷：“如果我要参加一个类似的小组来延长考试时间，我会得到相同的结果吗？” 这样的实验充其量只能得到相似的结果。 因此，正确的问题可能类似于“我的结论还成立吗？” 谨慎的决策者有几个危险等待着。

A first danger comes from the design and context of the experiment. Suppose you are given a billion dices, and that you roll each dice 10 times. If you get a dice that gave you ten times a 6, does it mean it is biased?This is possible, but on the other hand, the design of this experiment made it extremely likely to observe such an outlier, even if all dices are fair. In this case, the eleventh throw of this dice will likely not be a 6 again

第一个危险来自实验的设计和环境 。 假设给您十亿个骰子，并且将每个骰子掷10次。 如果您得到的骰子是6的10倍，是否表示它有偏见？这是可能的，但另一方面，本实验的设计使其极有可能观察到这样的异常值，即使所有骰子都是公平。 在这种情况下，此骰子的第11次掷出可能不再是6

A second danger comes from human factors. In particular incentives and cognitive bias.Cognitive bias, because when someone is convinced of something, he is more inclined to listen to — and report — a positive rather than a negative signal.Incentives, because society — shall it be in the workplace, the media or scientific communities — is more inclined to praise statistically positive results than negative ones.For instance, suppose an R&D team is working on a module improvement by doing A/B tests. Suppose also that positive outcomes are very unlikely, and negative ones very likely, and that the result of experiments is noisy. An incautious decision-maker is likely to roll out more negative experiments than positive ones, hence the overall effort of the R&D team will end up deteriorating the module.

第二个危险来自人为因素 。 特别是动机和认知偏见 。 认知偏见 ，因为当某人确信某件事时，他更倾向于倾听并报告正面的信号，而不是负面的信号。 激励措施是因为社会(无论是在工作场所，媒体还是科学界)都应该赞扬统计学上的积极结果，而不是消极的结果。例如，假设一个研发团队正在通过A / B测试来改进模块。 还假设积极的结果是极不可能的，而消极的结果是极有可能的，并且实验的结果是嘈杂的。 一个不谨慎的决策者可能会推出更多的负面实验，而不是正面的实验，因此研发团队的整体努力最终会使模块恶化。

At Criteo, we use A/B testing to make decision while coping with uncertainty. It is something we understand well because it is at the heart of our activities.Still, A/B testing raises many questions that are technically involved, and so require some math and statistical analysis. We propose to answer some of them in this blog post.

在Criteo，我们使用A / B测试来做出决策，同时应对不确定性。 我们很了解这是因为它是我们活动的核心。仍然，A / B测试提出了许多技术上涉及的问题，因此需要一些数学和统计分析。 我们建议在此博客文章中回答其中一些问题。

We will introduce several statistical tools to determine if an A/B-test is significant, depending on the type of metric we are looking at. We will focus first on additive metrics, where simple statistical tools give direct results, and then we will introduce the bootstrap method which can be used in more general settings.

我们将介绍几种统计工具来确定A / B检验是否有效，具体取决于我们正在查看的指标类型。 我们将首先关注简单的统计工具可直接得出结果的加性指标，然后我们将介绍可在更一般的设置中使用的引导方法。

如何总结A / B测试的重要性 (How to conclude on the significance of an A/B-test)

We will present good practices based on the support of the distribution (binary / non-binary) and on the type of metric (additive / non-additive).In the following sections, we will propose different techniques that allow us to assess if an A/B-test change is significant, or if we are not able to confidently conclude that the A/B-test had any effect.

我们将基于分布的支持(二进制/非二进制)和度量类型(加法/非加法)提出良好做法。在以下各节中，我们将提出不同的技术，使我们能够评估A / B测试更改意义重大，或者如果我们无法自信地得出结论，A / B测试有效。

We measure the impact of the change done in the A/B-test by looking at metrics. In the case of Criteo, this metric could for instance be “the number of sales made by a user on a given period”.

我们通过查看指标来衡量在A / B测试中所做更改的影响。 在Criteo的情况下，该指标例如可以是“用户在给定时期内的销售数量”。

We measure the same metric on two populations: The reference and the test population. Each population has a different distribution, from which we gather data points (and eventually compute the metric). We also assume that the A/B-test has separated the population randomly and that the measures are independent with respect to each other.

我们在两个总体上测量相同的指标：参考总体和测试总体。 每个总体都有不同的分布，从中我们可以收集数据点(并最终计算指标)。 我们还假设A / B检验已随机分离了总体，并且这些度量相对于彼此是独立的。

累加指标的一些特殊情况 (Some special cases for additive metrics)

Additive metrics can be computed at small granularity (for instance at the display or user level), and then summed up to form the final metric. Examples might include the total cost of an advertiser campaign (which is the sum of the cost of each display), or number of buyers for a specific partner.

可以以较小的粒度(例如在显示级别或用户级别)计算附加指标，然后将其加起来以形成最终指标。 例如，可能包括广告客户活动的总费用(即每次展示费用的总和)，或特定合作伙伴的购买者数量。

指标仅包含零或一 (The metric contains only zeros or ones)

At Criteo, we have quite a few binary metrics that we use for A/B-test decision making. For instance, we want to compare the number of users who clicked on an ad or better yet, the number of buyers in the two populations of the A/B-test. The base variable here is the binary variable X which represents if a user has clicked an ad or bought a product.

在Criteo，我们有很多二进制指标可用于A / B测试决策。 例如，我们要比较点击广告的用户数量或更好的用户，即A / B测试两个人群中的购买者数量。 这里的基本变量是二进制变量X，它表示用户是否单击了广告或购买了产品。

For this type of variable, the test to use is a chi-squared Pearson test.

对于此类变量，要使用的检验是卡方皮尔逊检验。

Let us say we want to compare the number of buyers between the reference population and the test population. Our null statistical hypothesis H0 is that the two populations have the same buying rate. The alternative hypothesis H1 is that the two populations do not have the same buying rate. We will fix the p-value to 0.05 for instance (meaning that we will accept a deviation of the test statistic to its 5% extremes under the null hypothesis before we reject it).

假设我们要比较参考人口和测试人口之间的购买者数量。 我们的无效统计假设H0是两个总体具有相同的购买率。 备选假设H1是两个总体的购买率不同。 例如，我们会将p值固定为0.05(这意味着在我们接受无效假设之前，我们将接受检验统计量与其5％极值之间的偏差)。

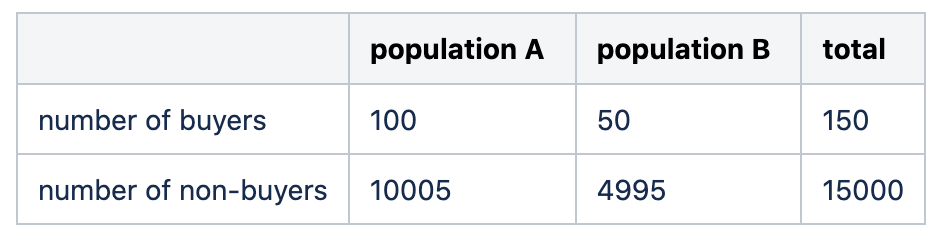
We have gathered the following data:

我们收集了以下数据：

Under the null hypothesis, population A and B are sampled from the same distribution, so that the empirical distribution of the sum of the two populations can be taken as the generative reference distribution. Here we get a conversion rate close to 1%.

在零假设下，从相同的分布中采样总体A和B，因此可以将两个总体之和的经验分布作为生成参考分布。 在这里，我们获得了接近1％的转化率。

Using this conversion rate for both populations, as the null hypothesis states, we can compute the expected distribution of buyers for populations A and B.

如原假设所述，使用两个人口的转换率，我们可以计算人口A和人口B的购买者的预期分布。

The chi-2 statistics is the sum, for all cells, of the square of the difference between the expected value and the real value, divided by the expected value. Here we get x2 = 0.743. We have chosen a p-value of 0.05, and thus for this two degree of freedom chi-2 distribution, the statistic needs to be inferior to 3.8. We accept the H0 hypothesis so that we deem this A/B-test as neutral.

chi-2统计量是所有单元格的期望值和实际值之差的平方的总和除以期望值。 在这里我们得到x2 = 0.743。 我们选择的p值为0.05，因此对于这两个自由度chi-2分布，统计量应低于3.8。 我们接受H0假设，因此我们认为此A / B检验为中性。

Note that this test naturally accommodates unbalanced populations (as here the population B is half the size of the population A).

请注意，此测试自然可以容纳不平衡的总体(因为此处的总体B是总体A的一半)。

加性指标的一般情况 (General case for an additive metric)

When the additive metric is not composed of only zeros and ones, the central limit theorem can be used to derive instantly the confidence interval of the metric. The central limit theorem tells us that the distribution of the mean of i.i.d. variables follows a normal distribution of known parameters. By multiplying by the total number of summed elements, this gives us the confidence bound for the sum.

当加性度量不仅由零和一组成时，可以使用中心极限定理立即导出度量的置信区间。 中心极限定理告诉我们， iid变量的均值分布遵循已知参数的正态分布。 通过将求和元素的总数乘以，便得出了求和结果的置信区间。

In the case of an A/B-test, things are a little bit more complicated as we need to compare two sums. Here, the test to use is a variant of the Student t-test. As the variance of the two samples are not expected to be the same, we have to use the specific version of the test which is adapted to this situation. It is called the Welch’s t-test. As for any statistical test, one needs to compute the statistic of the test, and compare it to the decision value given by the p-value chosen beforehand.

在A / B测试的情况下，由于我们需要比较两个总和，所以事情要复杂一些。 在这里，要使用的测试是Student t-test的变体。 由于两个样本的方差预计不会相同，因此我们必须使用适合这种情况的特定版本的测试。 这称为韦尔奇t检验 。 对于任何统计检验，都需要计算检验的统计量，并将其与预先选择的p值给出的决策值进行比较。

This method has a solid statistical basis and is computationally very efficient, as it only needs the mean and the variance of the statistic over the two populations.

该方法具有扎实的统计基础，并且计算效率很高，因为它只需要两个总体的统计量的均值和方差即可。

指标没有特殊属性 (The metric has no special property)

The bootstrap method enables to conclude in this general case. We will present two versions of it. First, we introduce the exact one, which happens to be non-distributed. To accommodate larger data sets, a distributed version will be presented afterwards.

引导程序方法可以在这种一般情况下得出结论。 我们将介绍它的两个版本。 首先，我们介绍确切的一个，它恰好是非分布式的。 为了容纳更大的数据集，之后将提供分布式版本。

引导程序方法(非分布式) (Bootstrap method (non-distributed))

Bootstrapping is a statistical method used for estimating the distribution of a statistic. It was pioneered by Efron in 1979. Its main strength is its ease of application on every metric, from the most simple to the most complicated. There are some metrics where you cannot apply the Central Limit Theorem, as for instance the median (or any quantile), or for a more business-related one, the cost per sale (it is a ratio of two sums of random variables). Its other strength lies in the minimal amount of assumptions needed to use it, which makes it a method of choice in most situations.

自举是一种统计方法，用于估计统计信息的分布。 它是埃夫隆(Efron)于1979年率先提出的。它的主要优点是易于在每个度量标准中使用，从最简单到最复杂。 在某些度量标准中，您无法应用中央极限定理，例如中位数(或任何分位数)，或者与业务相关的度量标准，即每次销售成本(它是两个随机变量之和的比率)。 它的其他优势在于使用它所需的最少假设量，这使其成为大多数情况下的一种选择方法。

The exact distribution of the metric can never be fully known. One good way to get it would be to reproduce the experiment which led to the creation of the data set many times and compute the metric each time. This would be of course extremely costly, not to mention largely impractical when an experiment cannot be run exactly the same twice (such as when some sort of feedback exists between the model being tested in the experiment and the results).

指标的确切分布永远无法完全了解。 获得它的一种好方法是重现导致多次创建数据集的实验，并每次计算度量。 当然这将是极其昂贵的，更不用说当实验不能完全相同地运行两次时(例如，当实验中的模型与结果之间存在某种反馈时)，这在很大程度上是不切实际的。

Instead, the bootstrap method starts from data set as an empirical distribution and replays “new” experiments by drawing samples (with replacement) from this data set. This is infinitely more practical than redoing the experiment many times. It has, of course, a computational cost of recreating (see below for a discussion of how many) an entire data set by sampling with replacement. The sampling is done using a binomial law of parameters (n, 1/n).

相反，bootstrap方法从数据集开始作为经验分布，并通过从该数据集中抽取样本(替换)来重放“新”实验。 这比多次重做实验更加实用。 当然，通过替换采样来重新创建整个数据集会产生一定的计算成本(请参阅下文中的讨论)。 使用参数(n，1 / n)的二项式定律进行采样。

引导方法：实用的演练 (Bootstrap method: A practical walk-through)

1. First, decide on the number k of bootstraps you want to use. A reasonable number should be at least a hundred, depending on the final use of the bootstraps.

   首先，确定您要使用的引导程序的数量k 。 合理的数量应至少为一百，这取决于引导程序的最终用途。

2. For every bootstrap to be computed, recreate a data set from the initial one with random sampling with replacement, this new data set having the same number of examples than the reference data set.
   对于要计算的每个引导程序，请从初始样本集重新创建一个数据集，并通过随机抽样进行替换，该新数据集的示例数与参考数据集相同。
3. Compute the metric of interest on this new data set.
   计算此新数据集上的关注指标。

4. Use the k values of the metric either to conclude on the statistical significance of the test.

   使用度量的k值可以得出测试的统计显着性。

在A / B测试的情况下如何使用引导程序 (How to use bootstraps in the case of an A/B-test)

When analyzing an A/B-test, there is not only one but two bootstraps to be made. The metric has to be bootstrapped on both populations. The bootstrapped difference of the metric between the two populations can be simply computed by subtracting the unsorted bootstraps of the metric of one population with the other. For additive metrics, this is equivalent to computing on the whole population a new metric which the same on one population and minus the previous one on the other population.

分析A / B测试时，不仅要进行一次引导，而且要进行两次引导。 该指标必须在两个人群中都具有优势。 可以通过将一个总体的指标的未排序引导程序与另一个总体相减来简单计算两个指标之间的自举差异。 对于加性指标，这等效于在整个总体上计算一个新指标，该新指标在一个总体上相同，而在另一个总体上减去前一个指标。

The bootstrapping has to be done in a fashion compatible with the split used for the A/B-test. Let us illustrate this by an example. At Criteo, we do nearly all our A/B-tests on users. We also think that most of the variability we see in our metrics comes from the users, so we bootstrap our metrics on users.

自举必须以与用于A / B测试的拆分兼容的方式进行。 让我们通过一个例子来说明这一点。 在Criteo，我们几乎对用户进行所有A / B测试。 我们还认为，我们在指标中看到的大多数可变性都来自用户，因此我们将指标引导到用户身上。

Finally, if the populations have different sizes, additive metrics need to be normalized so that the smaller population is comparable to the larger. This is not neccessary for intensive metrics (such as conversion rate or averages). For instance, to compare the effect of lighting conditions on the number of eggs laid in two different chicken coops, one larger than the other, the number of eggs has to be resized so that the two chicken coops are made of the same arbitrary size (note that here, we do not resize the number of chicken, as there might be no fixed relation between the size of the coop and the number of chicken). But studying the average number of eggs laid by every hen, no such resizing is needed (as it is already done by the averaging).

最后，如果总体大小不同，则需要对附加指标进行标准化，以便较小的总体与较大的总体具有可比性。 对于密集指标(例如转化率或平均值)，这不是必需的。 例如，为了比较光照条件对两个不同鸡舍产下的鸡蛋数量(一个大于另一个)的影响，必须调整鸡蛋的大小，以使两个鸡舍都具有相同的任意大小(请注意，在这里，我们没有调整鸡的数量，因为鸡舍的大小和鸡的数量之间可能没有固定的关系。 但是，通过研究每只母鸡产下的鸡蛋的平均数量，就不需要进行这种大小调整(因为平均已经完成了)。

如何得出A / B检验的重要性的结论？ (How to conclude on the significance of the A/B-test?)

The bootstrap method gives an approximation of the distribution of the metric. This can be used directly in a statistical test, either non-parametric or parametric. For instance, given the distribution of the difference of some metric between the two populations, a non-parametric test would be, given H0 “the two population are the same, ie the difference of the metric should be zero” and a p-value of 0.05, to compute the quantiles [ 2.5%, 97.5%] by ordering the bootstrapped metric, and conclude that H0 is true if 0 is inside this confidence interval. Other methods exist for computing a confidence interval from a bootstrapped distribution. A parametric test would for example interpolate the distribution of the metric by a normal one (using the mean and the variance computed from the bootstraps) and conclude that H0 is true if 0 is less than (approximately) two standard deviations away from the mean. This is true only for metrics whose distribution is approximately normal (for instance a mean value, where the central limit theorem will apply).

引导程序方法给出了度量分布的近似值。 这可以直接用于非参数或参数的统计测试中。 例如，给定两个总体之间某个度量标准差的分布，则给定H0，“两个总体相同，即度量标准差应为零”，并给出p值，这将是一个非参数检验。取0.05，以通过对自举度量进行排序来计算分位数[2.5％，97.5％]，并得出结论，如果0在此置信区间内，则H0为真。 存在用于根据自举分布计算置信区间的其他方法 。 例如，参数测试将通过一个正态插值来度量的分布(使用均值和自举计算得出的方差)，并得出结论：如果0小于(近似)远离均值的两个标准差，则H0为真。 这仅适用于分布近似正态的度量(例如，平均值，将应用中心极限定理)。

图解的例子 (An illustrated example)

To explain how to use the bootstrap method for A/B-testing, let us go through a very easy example. Two populations A and B have both one million users each, and we are looking at the number of people who bought a product. For our synthetic example, population A has a conversion rate of exactly one percent, whereas population B has a conversion rate of 1.03%. We simulate the two datasets using Bernouilli trials, and end up with 10109 buyers in population A, and 10318 buyers in population B. Note that the empirical conversion rate of population A deviates far more from the true rate than for population B. The question asked is “Is the difference of the number of buyers significant?”. The null hypothesis is that the two populations are generated from the same distribution. We will take a confidence interval of [2.5%; 97.5%] to conclude.

为了说明如何使用引导方法进行A / B测试，我们来看一个简单的示例。 A和B这两个人群分别拥有100万用户，我们正在研究购买产品的人数。 对于我们的综合示例，群体A的转化率恰好为1％，而群体B的转化率为1.03％。 我们使用Bernouilli试验模拟这两个数据集，最终得到人口A的10109个购买者和人口B的10318个购买者。请注意，人口A的经验转化率与真实比率的偏离远大于人口B的真实转化率。是“购买者数量差异显着吗？”。 零假设是两个总体由相同的分布生成。 我们将置信区间为[2.5％； 97.5％]得出结论。

We use a thousand bootstraps to see the empirical distribution of the number of buyers in both populations. Here is a plot below of the histogram of the bootstraps:

我们使用一千个引导程序来查看两个人群中购买者数量的经验分布。 这是引导程序直方图的下方图：

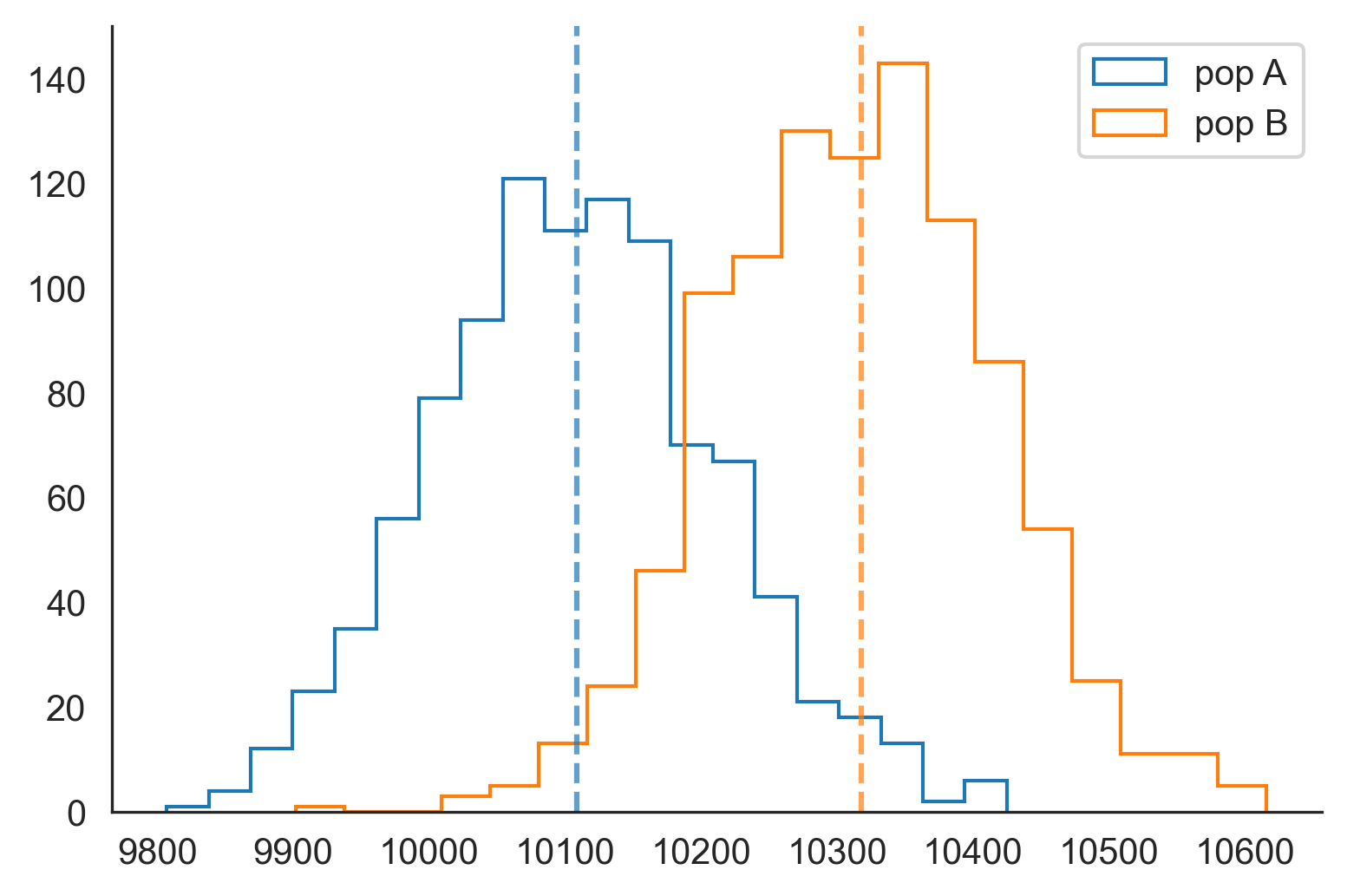
As predicted by the central limit theorem, the distributions are roughly normal and centered around the empirical number of buyers (dashed vertical lines). The two distributions overlap.

正如中心极限定理所预测的那样，分布大致呈正态分布，并以购买者的经验数量为中心(垂直虚线)。 这两个分布重叠。

To find the distribution of the difference of the number of buyers, the bootstraps of both populations are randomly shuffled and subtracted one by one. Another way to look at it is to concatenate the two data sets together and create a metric with a +1 for a buyer in A and -1 for a buyer in B. The sum of this metric gives the difference of number of buyers in the two populations. If the random sampling is compatible with the population split, this gives exactly the same result. Below is the result of this operation. As expected by the central limit theorem, this is a normal distribution. The color indicates if a bootstrap is positive or negative.

为了找到购买者数量差异的分布，随机调整两个种群的引导程序，并一一减去。 另一种看待它的方法是将两个数据集连接在一起，并创建一个度量标准，其中A中的买方为+ 1，B中的买方为-1。该度量的总和给出了A中买方的数量差异。两个人口。 如果随机抽样与总体划分兼容，则得出的结果完全相同。 以下是此操作的结果。 正如中心极限定理所期望的，这是一个正态分布。 颜色指示引导程序是正还是负。

In this case, the number of positive bootstraps is 74 out of 1000. This means that only 7.4% of bootstraps show a positive difference inside the confidence interval of [2.5%; 97.5%] which we decided earlier on. Subsequently, we cannot reject the null hypothesis. We can only say that the A/B-test is inconclusive.

在这种情况下，正引导程序的数量为1000的74。这意味着，只有7.4％的引导程序在置信区间[2.5％; 97.5％]。 随后，我们不能拒绝原假设。 我们只能说A / B测试没有定论。

Bootstrap方法(分布式) (Bootstrap method (distributed))

When working with large-scale data, several things can happen to the data set:

当使用大规模数据时，数据集可能会发生几件事情：

• The data set is distributed across machines and too big to fit into a single’s machine memory
  数据集分布在计算机之间，并且太大而无法容纳一个人的计算机内存
• The data set is distributed across machines and even though it could fit into a single machine, it is costly and impractical to collect everything on a single machine
  数据集分布在多台计算机上，即使它可以放入一台计算机中，也要在一台计算机上收集所有数据，这既昂贵又不切实际

• The data set is distributed across machines and even the values of an observation are distributed across machines. For instance, it happens if the observation we are interested in is “how much did the user spend for all his purchases in the last 7 days” and if our data set contains data at purchase-level. To apply the previous methods, we would first need to regroup our purchase-level data set into a user-level data set, which can be costly.

  该数据集跨机器分布和观察甚至值被跨越机器分布。 例如，如果我们感兴趣的观察结果是“用户在过去7天内花了多少钱购买所有商品”并且我们的数据集包含购买级别的数据，就会发生这种情况。 要应用先前的方法，我们首先需要将购买级别的数据集重新分组为用户级别的数据集，这可能会花费很大。

In this section, we describe a bootstrap algorithm that can work in this distributed setting. As it is also able to work on any distribution type, it is thus the most general algorithm to get confidence intervals.Let us first define k, the number of resamplings that we will do over the distribution of X (usually, at least 100). To get S1, the sum of the first resampled draw, we would normally draw with replacement n elements from the series of X_i, and then sum them.

在本节中，我们描述了可以在此分布式设置中工作的引导程序算法。 由于它也可以处理任何分布类型，因此它是获取置信区间的最通用算法。让我们首先定义k，即在X的分布上(通常至少100)进行重采样的次数。 。 为了得到S1，即第一次重采样的和，我们通常用X_i系列中的替换n个元素进行绘画，然后将它们求和。

However, in a distributed setting, it might be impossible or too costly to do a draw with replacement of the distributed series X_i. We instead use an approximation: Sum each element of the data set, weighted with a weight drawn from a Poisson(1) distribution. This weight is also “seeded” by both; the bootstrap population id (so from 1 to k) and also an identifier that represents the aggregation level our data should be grouped by. Doing this ensures that, if we go by the previous example, purchases made by the same user get the same weight for a given bootstrap resampling: We get the same end result as if we had already grouped the data set by user in the first place.

但是，在分布式环境中，用替换分布式系列X_i进行抽奖可能是不可能的，或者成本太高。 相反，我们使用一个近似值：对数据集的每个元素求和，并使用从Poisson(1)分布中得出的权重进行加权。 双方也都“担负”了这一责任； 引导程序人口ID(从1到k)，以及代表我们的数据应归类的聚合级别的标识符。 这样做可以确保，如果我们按照前面的示例进行操作，则在给定的引导程序重采样下，同一用户购买的商品将获得相同的权重：我们得到的最终结果与首先将用户对数据集进行分组的结果相同。

We thus obtain S1, an approximate version of the sum from resampled data. Once we obtain the S1… S_k series, we use this as a proxy for the real distribution of S and can then take the quantiles from this series. Note that this raises 2 issues:

因此，我们从重新采样的数据中获得S1，即总和的近似版本。 一旦获得S1…S_k系列，就可以将其用作S实际分布的代理，然后可以从该系列中获取分位数。 请注意，这引起了两个问题：

• An approximation error is made due to the fact that the number of bootstraps is finite (the bootstrap method converges for an infinite number of resampling)
  由于引导程序的数量是有限的，所以会产生近似误差(引导程序方法收敛于无限数量的重采样)

• An approximation error that induces a bias in the measure of quantiles is made due to the fact that the resampling is done approximately. This comes from the fact that for a given resampling, the sum of the weights is not exactly equal to n (this is only true on average). For further reading, check out this great blog post and the associated scientific paper.

  由于重采样是近似完成的，所以会产生一个近似误差，该误差会导致分位数的度量产生偏差。 这源于以下事实：对于给定的重采样，权重的总和不完全等于n(这仅在平均值上正确)。 如需进一步阅读，请查看这篇出色的博客文章和相关的科学论文 。

摘要 (Summary)

比较利弊 (Comparative pro/cons)

Here is a short table highlighting the pros and cons of each method.

这是一张简短的表格，突出了每种方法的优缺点。

结论 (Conclusion)

In this article, we have detailed how to analyze A/B-tests using various methods, depending on the type of metric which is analyzed and the amount of data. While all methods have their advantages and their drawbacks, we tend to use bootstraps most of the time at Criteo, because it is usable in most cases and lends itself well to distributed computing. As our data sets tend to be very large, we always use the distributed bootstraps method. We would not be able to afford the numerical complexity of the exact bootstrap method.

在本文中，我们详细介绍了如何根据所分析的指标类型和数据量，使用各种方法来分析A / B测试。 尽管所有方法都有其优点和缺点，但我们大多数时候倾向于在Criteo中使用引导程序，因为它在大多数情况下都可用并且非常适合于分布式计算。 由于我们的数据集往往非常大，因此我们始终使用分布式引导程序方法。 我们将无法负担精确自举方法的数值复杂性。

We also think that using the Chi-2 and T-test methods from time to time is useful. Using these methods forces you to follow the strict statistical hypothesis testing framework, and ask yourself the right questions. As you may find yourself using the bootstrap method a lot, it allows to keep a critical eye on it, and not take blindly its figures for granted!

我们还认为，不时使用Chi-2和T检验方法是有用的。 使用这些方法会迫使您遵循严格的统计假设检验框架，并向自己提出正确的问题。 您可能会发现自己经常使用bootstrap方法，因此它可以使您始终保持批判的眼光，而不会盲目地将其数字视为理所当然！

关于作者 (About the authors)

Aloïs Bissuel, Vincent Grosbois and Benjamin Heymann work in the same team at Criteo, working on measuring all sorts of things.

AloïsBissuel，Vincent Grosbois和Benjamin Heymann在Criteo的同一团队中工作，致力于测量各种事物。

Benjamin Heymann is a senior researcher, while Aloïs Bissuel and Vincent Grosbois are both senior machine learning engineers.

Benjamin Heymann是高级研究员，而AloïsBissuel和Vincent Grosbois都是高级机器学习工程师。

Like what you are reading? Check out our latest articles on Medium.

喜欢您正在阅读的内容吗？ 查看我们有关Medium的最新文章。

Interested in joining Criteo and help continue this article? Check out our current openings!

有兴趣加入Criteo并帮助继续本文吗？ 查看我们当前的空缺！