直方图及直方图均值化的理论,实现及展示
直方图:
首先,我们来看看什么是直方图:
理论概念:
在图像处理中,经常用到直方图,如颜色直方图、灰度直方图等。 图像的灰度直方图就描述了图像中灰度分布情况,能够很直观的展示出图像中各个灰度级所 占的多少。 图像的灰度直方图是灰度级的函数,描述的是图像中具有该灰度级的像素的个数:其中,横 坐标是灰度级,纵坐标是该灰度级出现的频率。
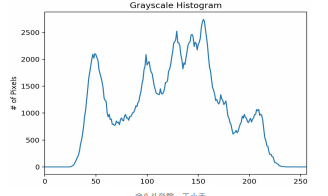
意义:
• 直方图反映了图像中的灰度分布规律。它描述每个灰度级具有的像素个数,但不包含 这些像素在图像中的位置信息。
• 任何一幅特定的图像都有唯一的直方图与之对应,但不同的图像可以有相同的直方图。
• 如果一幅图像有两个不相连的区域组成,并且每个区域的直方图已知,则整幅图像的 直方图是该两个区域的直方图之和
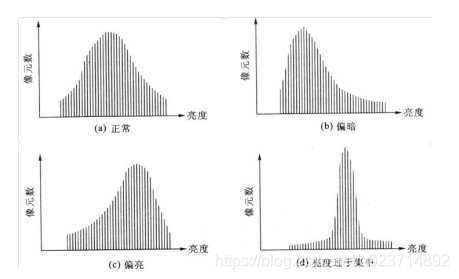
代码实现:
import cv2
import numpy as np
from matplotlib import pyplot as plt'''
calcHist—计算图像直方图
函数原型:calcHist(images, channels, mask, histSize, ranges, hist=None, accumulate=None)
images:图像矩阵,例如:[image]
channels:通道数,例如:0
mask:掩膜,一般为:None
histSize:直方图大小,一般等于灰度级数
ranges:横轴范围
'''
'''
# 灰度图像直方图
# 获取灰度图像
img = cv2.imread("lenna.png", 1)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#cv2.imshow("image_gray", gray)# 灰度图像的直方图,方法一
plt.figure()
plt.hist(gray.ravel(), 256)
plt.show()'''
'''
# 灰度图像的直方图, 方法二
hist = cv2.calcHist([gray],[0],None,[256],[0,256])
plt.figure()#新建一个图像
plt.title("Grayscale Histogram")
plt.xlabel("Bins")#X轴标签
plt.ylabel("# of Pixels")#Y轴标签
plt.plot(hist)
plt.xlim([0,256])#设置x坐标轴范围
plt.show()
'''#彩色图像直方图
image = cv2.imread("lenna.png")
cv2.imshow("Original",image)
#cv2.waitKey(0)chans = cv2.split(image)
colors = ("b","g","r")
plt.figure()
plt.title("Flattened Color Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")for (chan,color) in zip(chans,colors):hist = cv2.calcHist([chan],[0],None,[256],[0,256])plt.plot(hist,color = color)plt.xlim([0,256])
plt.show()
运行结果:
彩色:
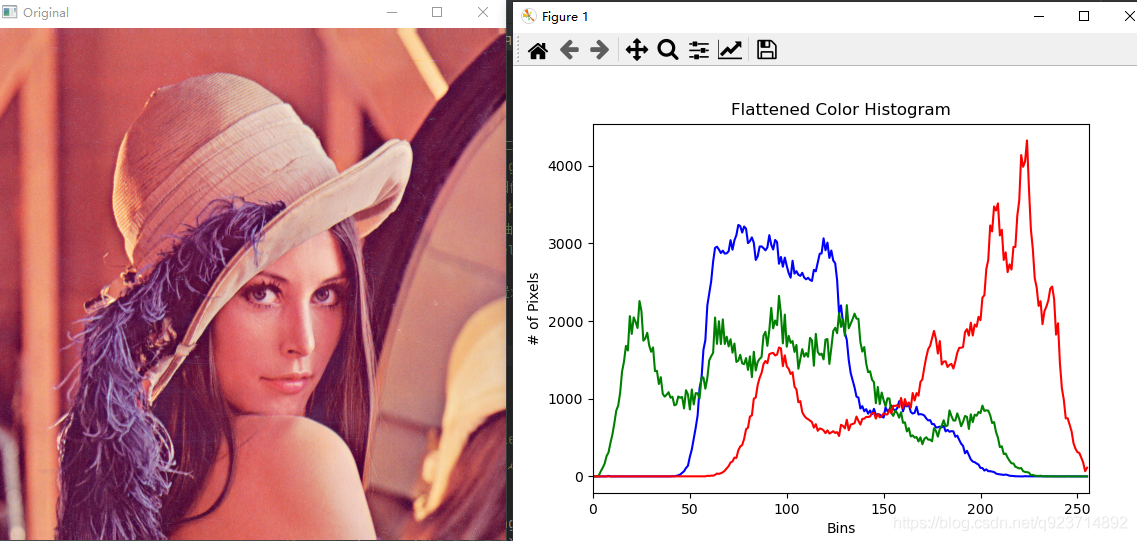
灰色:
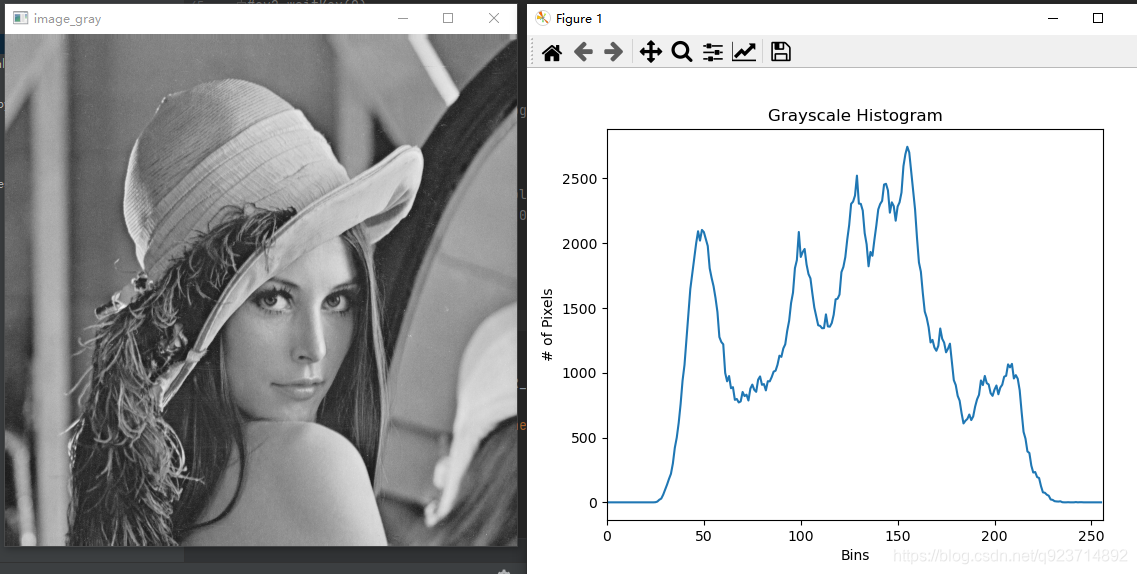
直方图均值化
由上面的输出结果,我们很容易发现,像素的分布是不均匀的,我们需要将像素的分布变得均匀,这就用到了直方图均值化。
概念:
直方图均衡化是将原图像的直方图通过变换函数变为均匀的直方图,然后按均匀直方图修改原 图像,从而获得一幅灰度分布均匀的新图像。
直方图均衡化的作用是图像增强。
步骤:
为了将原图像的亮度范围进行扩展,需要一个映射函数,将原图像的像素值均衡映射到新直 方图中,这个映射函数有两个条件: (1)为了不打乱原有的顺序,映射后亮、暗的大小关系不能改变, (2) 映射后必须在原有的范围内,比如(0-255)
步骤:
- 依次扫描原始灰度图像的每一个像素,计算出图像的灰度直方图H
- 计算灰度直方图的累加直方图
- 根据累加直方图和直方图均衡化原理得到输入与输出之间的映射关系。
- 最后根据映射关系得到结果:dst(x,y) = H’(src(x,y))进行图像变换
理论公式:
1.对于输入图像的任意一个像素p, p∈[0,255], 总能在输出图像里有对应的像素q, q∈[0,255] 使得下面等式成 立(输入和输出的像素总量相等):
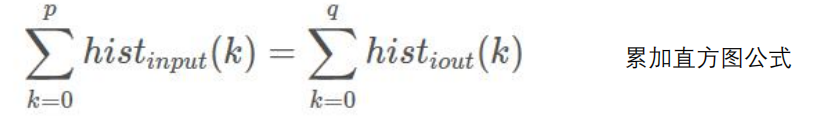
2.其中,输出图像每个灰度级的个数:
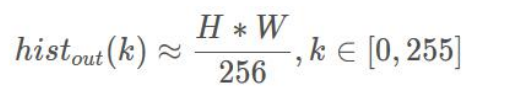
3.代入累加直方图公式:

(因为k是从0开始的,所以是乘(q+1),H和W分别为图像像素长和宽)
最后用一张图来讲解一下:
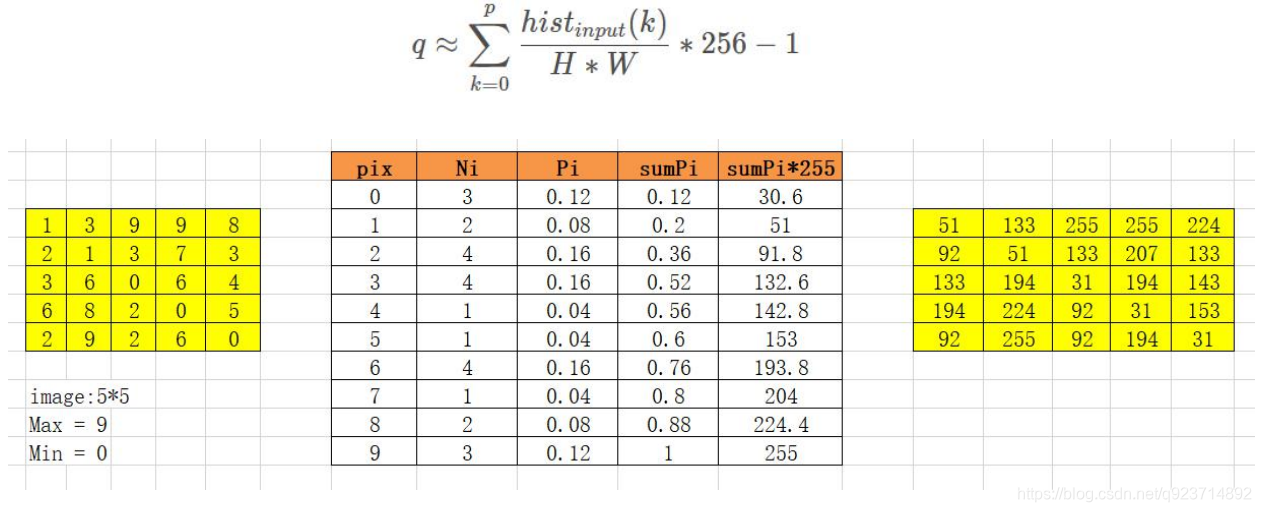
如左边黄色55图像中,像素值从0-9。
为其建立一个矩阵,pix值从0-9。
Ni值为该像素值存在的个数,如在55的图像中,0像素有3个,Ni值为3。
Pi值为该像素值的概率,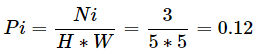
sunmPi值就是之前Pi的总和,也可以看作sumPi=Pi+sumP(i-1),比如sumP0=P0=0.12,sumP1=sumP0+P1
最后的结果就是sumPi×255-1(注意:图中忘记减一了)*,将这个结果的数值替换原像素数值。
代码实现:
import cv2
import numpy as np
from matplotlib import pyplot as plt'''
equalizeHist—直方图均衡化
函数原型: equalizeHist(src, dst=None)
src:图像矩阵(单通道图像)
dst:默认即可
'''# # 获取灰度图像
# img = cv2.imread("lenna.png", 1)
# gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# #cv2.imshow("image_gray", gray)
#
# # 灰度图像直方图均衡化
# dst = cv2.equalizeHist(gray)
#
# # 直方图
# hist = cv2.calcHist([dst],[0],None,[256],[0,256])
#
# plt.figure()
# plt.hist(dst.ravel(), 256)
# plt.show()
#
# cv2.imshow("Histogram Equalization", np.hstack([gray, dst]))
# cv2.waitKey(0)# 彩色图像直方图均衡化
img = cv2.imread("lenna.png", 1)
cv2.imshow("src", img)# 彩色图像均衡化,需要分解通道 对每一个通道均衡化
(b, g, r) = cv2.split(img)
bH = cv2.equalizeHist(b)
gH = cv2.equalizeHist(g)
rH = cv2.equalizeHist(r)
# 合并每一个通道
result = cv2.merge((bH, gH, rH))
cv2.imshow("dst_rgb", result)cv2.waitKey(0)chans = cv2.split(result)
colors = ("b","g","r")
plt.figure()
plt.title("Flattened Color Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")for (chan,color) in zip(chans,colors):hist = cv2.calcHist([chan],[0],None,[256],[0,256])plt.plot(hist,color = color)plt.xlim([0,256])
plt.show()
运行结果:
彩色:
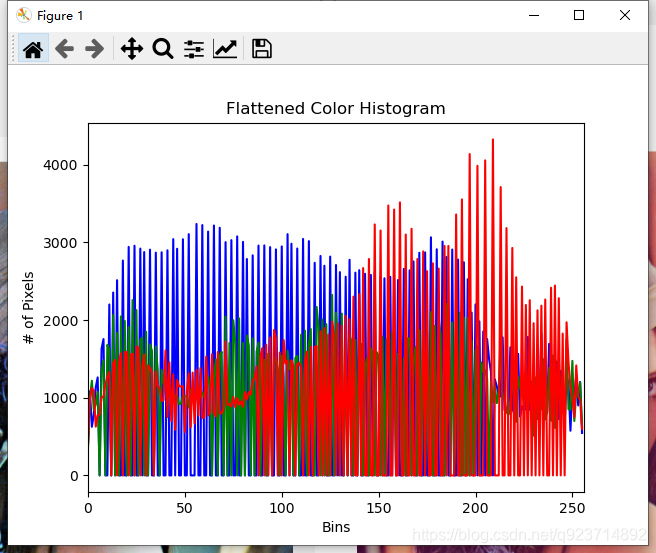
灰色:

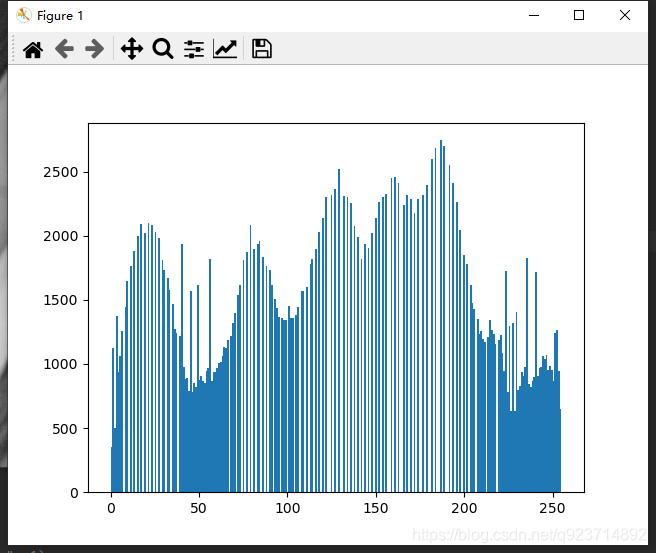
结果对比很明显像素值变的均匀很多,而且明显彩色图像变得更亮了一些。

)
填充与Vaild(有效)填充)


)













