opencv：畸变矫正：透视变换算法的思想与实现

畸变矫正

在这里插入图片描述
注意：虽然能够成功矫正但是也会损失了部分图像！

透视变换(Perspective Transformation)

概念：

透视变换是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。我们常说的仿射变换是透视变换的一个特例。透视变换的目的就是把现实中为直线的物体，在图片上可能呈现为斜线，通过透视变换转换成直线的变换。仿射变换（Affine Transformation或 Affine Map），又称为仿射映射，是指在几何中，图像进行从一个向量空间进行一次线性变换和一次平移，变换为到另一个向量空间的过程。
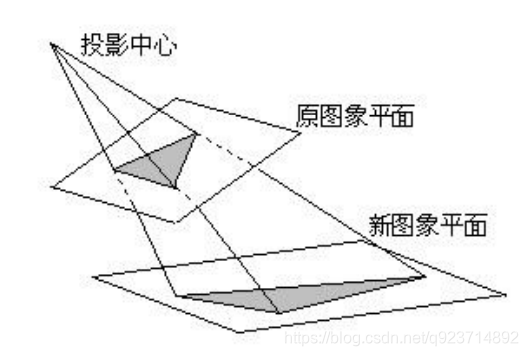
在这里插入图片描述

思想：

通用的变换公式为：
在这里插入图片描述
x,y是原始图片坐标，对应得到变换后的图片坐标（X’;Y’;Z’）其中：

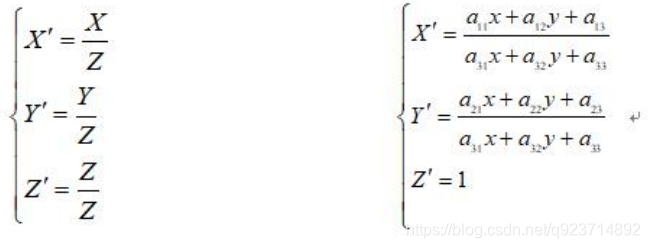
可以看作原图像的数据各值与变换后图像的数据各值，对应相等。
令a33=1，展开上面公式，得到一个点的情况：

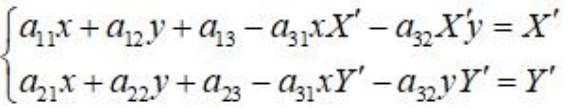
如果我们要解出上面含有8个未知量（a）的方程,我们需要8个像素点，原图像4个，新图像4个。
源点四个坐标分别为A：（x0,y0),(x1,y1),(x2,y2),(x3,y3) 目标点四个坐标分别为B：(X’0,Y’0),(X’1,Y’1),(X’2,Y’2),(X’3,Y’3)
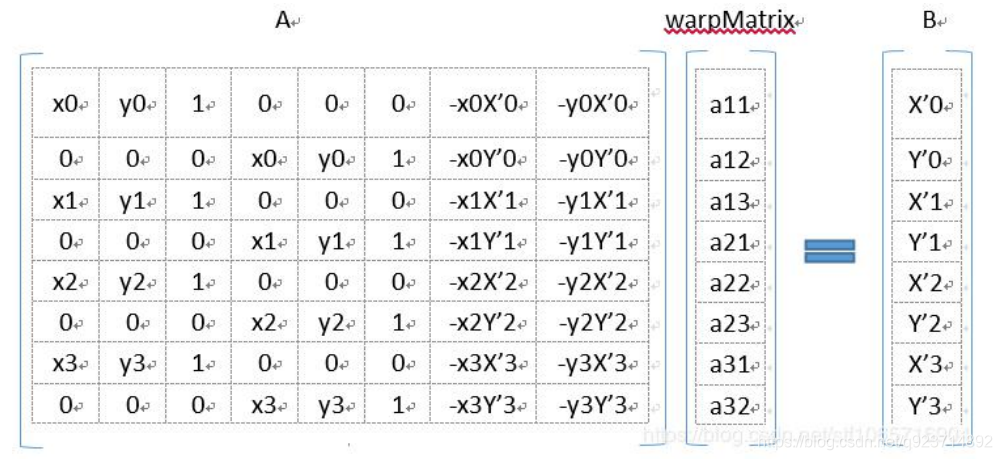
在这里插入图片描述

手动代码实现：

import numpy as npdef WarpPerspectiveMatrix(src, dst):assert src.shape[0] == dst.shape[0] and src.shape[0] >= 4#assert:当src的格式等于dst的格式，并且src的格式大于等于4，程序才继续运行nums = src.shape[0]A = np.zeros((2*nums, 8)) # A*warpMatrix=BB = np.zeros((2*nums, 1))for i in range(0, nums):A_i = src[i,:]B_i = dst[i,:]A[2*i, :] = [A_i[0], A_i[1], 1, 0, 0, 0,-A_i[0]*B_i[0], -A_i[1]*B_i[0]]B[2*i] = B_i[0]A[2*i+1, :] = [0, 0, 0, A_i[0], A_i[1], 1,-A_i[0]*B_i[1], -A_i[1]*B_i[1]]B[2*i+1] = B_i[1]A = np.mat(A)#用A.I求出A的逆矩阵，然后与B相乘，求出warpMatrixwarpMatrix = A.I * B #求出a_11, a_12, a_13, a_21, a_22, a_23, a_31, a_32#之后为结果的后处理warpMatrix = np.array(warpMatrix).T[0]warpMatrix = np.insert(warpMatrix, warpMatrix.shape[0], values=1.0, axis=0) #插入a_33 = 1warpMatrix = warpMatrix.reshape((3, 3))return warpMatrixif __name__ == '__main__':print('warpMatrix')src = [[10.0, 457.0], [395.0, 291.0], [624.0, 291.0], [1000.0, 457.0]]  #编造的输入src = np.array(src)dst = [[46.0, 920.0], [46.0, 100.0], [600.0, 100.0], [600.0, 920.0]]    #编造的输出dst = np.array(dst)warpMatrix = WarpPerspectiveMatrix(src, dst)print(warpMatrix)

这里就不展示结果了重点是思想

opencv接口代码实现：

import cv2
import numpy as npimg = cv2.imread('photo1.jpg')result3 = img.copy()#img = cv2.GaussianBlur(img,(3,3),0)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
#转灰度，做单通道计算比较节省时间
edges = cv2.Canny(gray,50,150,apertureSize = 3)
#canny边缘检测（仅针对这次的输入图片）
cv2.imshow("canny", edges)'''
注意这里src和dst的输入并不是图像，而是图像对应的顶点坐标。
'''
src = np.float32([[207, 151], [517, 285], [17, 601], [343, 731]])
dst = np.float32([[0, 0], [337, 0], [0, 488], [337, 488]])
# 生成透视变换矩阵；进行透视变换
m = cv2.getPerspectiveTransform(src, dst)
result = cv2.warpPerspective(result3, m, (337, 488))
# (337,488)是输出图像大小
cv2.imshow("src", img)
cv2.imshow("result", result)
cv2.waitKey(0)