Multicollinearity is likely far down on a mental list of things to check for, if it is on a list at all. This does, however, appear almost always in real-life datasets, and it’s important to be aware of how to address it.

多重共线性可能根本不在要检查的事物的清单上，即使它根本不在清单上。 但是，这几乎总是出现在现实生活的数据集中，因此，重要的是要知道如何解决它。

As its name suggests, multicollinearity is when two (or more) features are correlated with each other, or ‘collinear’. This occurs often in real datasets, since one measurement (e.g. family income) may be correlated with another (e.g. school performance). You may be unaware that many algorithms and analysis methods rely on the assumption of no multicollinearity.

顾名思义，多重共线性是指两个(或多个)要素相互关联，即“共线性”。 由于一种度量(例如家庭收入)可能与另一种度量(例如学校成绩)相关，因此这经常发生在真实数据集中。 您可能没有意识到许多算法和分析方法都依赖于没有多重共线性的假设。

Let’s take this dataset for example, which attempts to predict a student’s chance of admission given a variety of factors.

让我们以这个数据集为例，该数据集尝试在各种因素的影响下预测学生的入学机会。

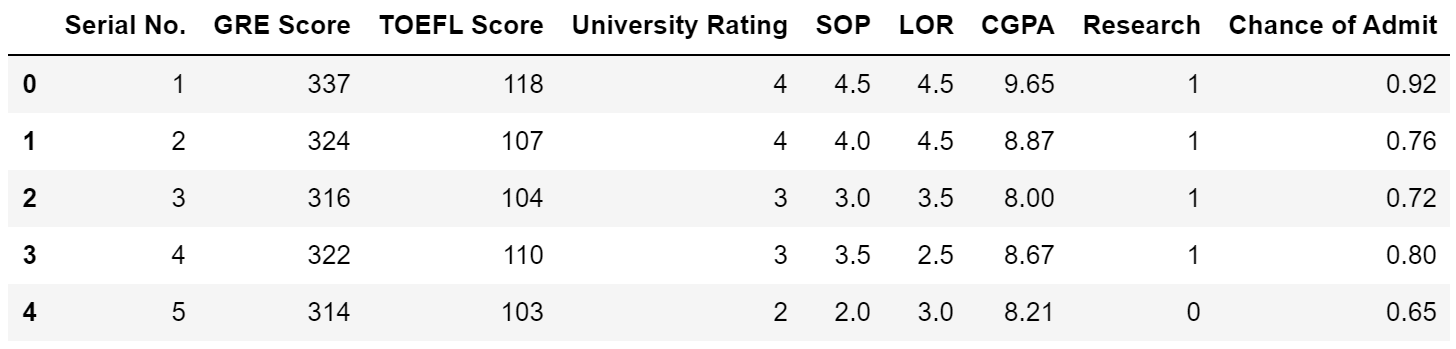
We want to achieve a static like “performing research increases your chance of admission by x percent” or “each additional point on the TOEFL increases chance of admission by y percent”. The first thought is to train a linear regression model and interpret the coefficients.

我们希望实现一个静态的状态，例如“进行研究使您被录取的机会增加x ％”或“托福每增加一个点，就可以使入学的机会增加y ％”。 首先想到的是训练线性回归模型并解释系数。

A multiple regression model achieves a mean absolute error of about 4.5% percentage points, which is fairly accurate. The coefficients are interesting to analyze, and we can make a statement like ‘each point on the GRE increases you chances of admission by 0.2%, whereas each point on your CGPA increases chances by 11.4%.’

多元回归模型的平均绝对误差约为4.5％，这是相当准确的。 系数的分析很有趣，我们可以做出这样的表述：“ GRE的每个点使您被录取的机会增加了0.2％，而CGPA的每个点使您被录取的机会增加了11.4％。”

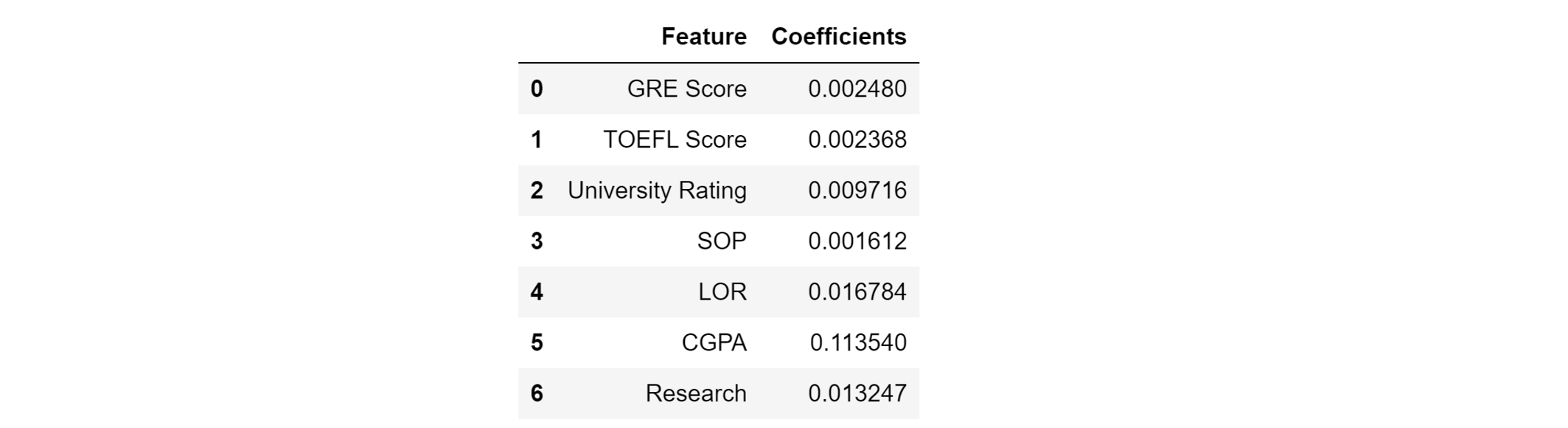
Let’s take a look at the correlation matrix to identify which features are correlated with each other. In general, this dataset is full of highly correlated features, but CGPA is in general correlated heavily with other features.

让我们看一下相关矩阵，以确定哪些要素相互关联。 总的来说，该数据集充满了高度相关的特征，但是CGPA通常与其他特征高度相关。

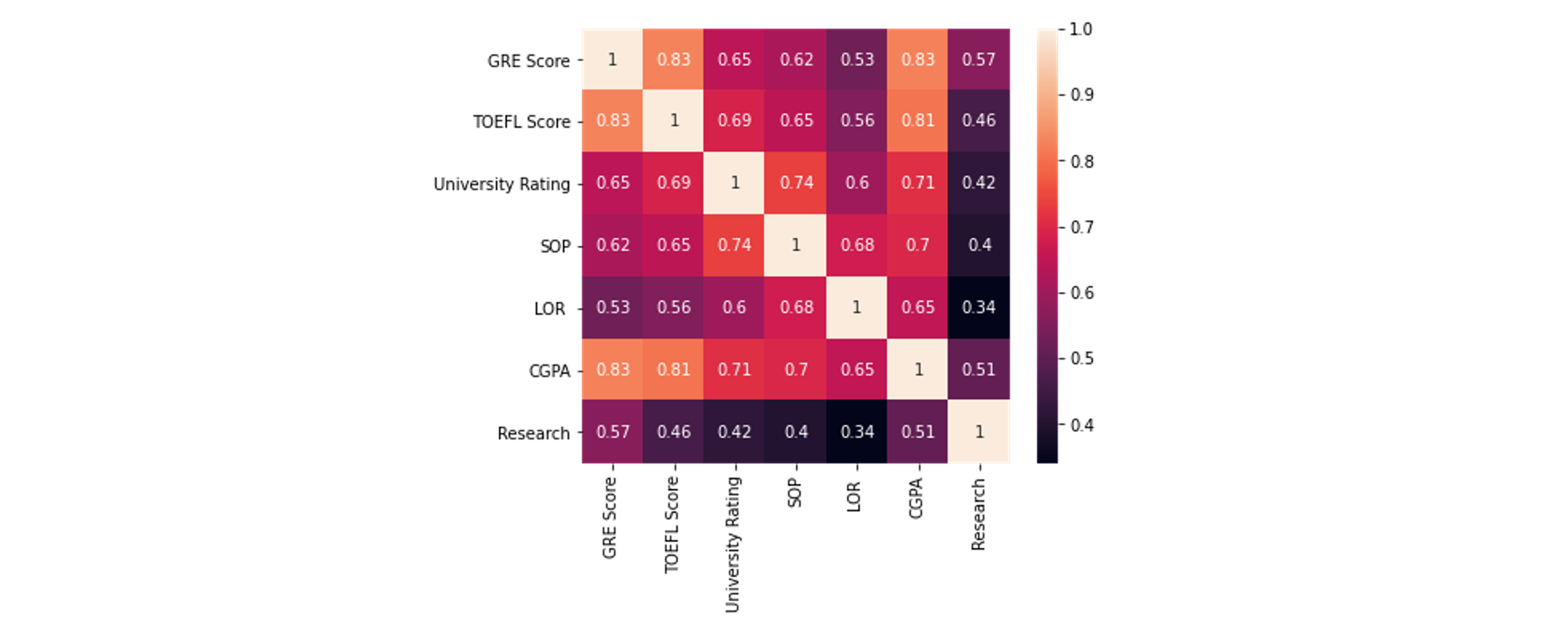
Since the TOEFL score is highly correlated by the GRE score, let’s remove this feature and re-train a linear regression model. (Perhaps) Surprisingly, the mean absolute error decreases to 4.3%. The change of coefficients is also interesting — notably, the importance of the University Rating decreases by almost half, the importance of research doubles, etc.

由于TOEFL分数与GRE分数高度相关，因此让我们删除此功能并重新训练线性回归模型。 (也许)令人惊讶的是，平均绝对误差降低到4.3％。 系数的变化也很有趣-值得注意的是，大学评估的重要性降低了近一半，研究的重要性增加了一倍，等等。

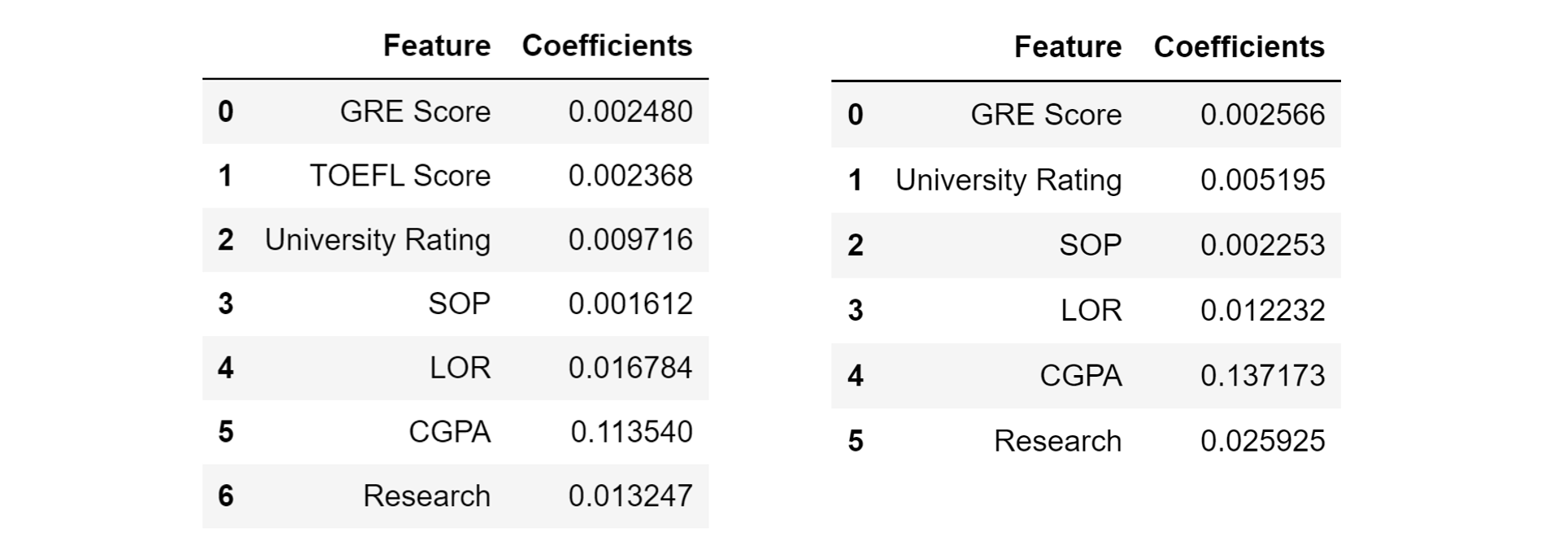
We can take the following away from this:

我们可以采取以下措施：

• The TOEFL score, like any other feature, can be thought of as having two components: information and noise.
  就像其他任何功能一样，TOEFL分数也可以认为具有两个组成部分：信息和噪音。
• Its information component was already represented in other variables (perhaps performing well on the GRE requires skills to perform well on the TOEFL, etc.), so it did not provide any new information.
  它的信息部分已经用其他变量表示(也许在GRE上表现出色需要技能才能在TOEFL上表现出色，等等)，因此它没有提供任何新信息。
• It had enough noise such that keeping the feature for a minimal information gain is not worth the amount of noise it introduces to the model.
  它具有足够的噪声，以至于为了获得最小的信息增益而保持该功能不值得其引入模型的噪声量。

In other words, the TOEFL score was collinear with many of the other features. At a base level, the performance of the model was damaged, but additionally, more complex analyses on linear models — which can be very insightful — like the interpretation of coefficients need to be adjusted.

换句话说，托福成绩与许多其他特征是共线的。 从根本上来说，模型的性能受到了损害，但此外，对线性模型的更复杂的分析(可能非常有见地)也需要调整，例如系数的解释需要调整。

It’s worth exploring what the coefficients of regression models mean. For instance, if the coefficient for GRE score is 0.2%, this means that holding all other variables fixed, a one-unit increase in GRE score translates to a 0.2% increase in admission. If we include the TOEFL score (and additional highly correlated features), however, we can’t assume that these variables will remain fixed.

值得探索回归模型系数的含义。 例如，如果GRE分数的系数为0.2％，则意味着将所有其他变量固定为 ，GRE分数每增加1单位，入学率就会增加0.2％。 但是，如果我们包括TOEFL分数(以及其他高度相关的功能)，则不能假定这些变量将保持不变。

Hence, the coefficients go haywire, and completely uninterpretable, since there is massive information overlap. When such scenarios arise, the modelling capability is limited as well. Because there is so much overlap, everything is amplified — if there is an error in one part, it is likely to spread via overlapping to several other sections.

因此，由于存在大量的信息重叠，因此这些系数非常困难，并且完全无法解释。 当出现这种情况时，建模能力也会受到限制。 由于存在太多的重叠，因此一切都会被放大-如果一个部分中存在错误，则很可能会通过重叠到其他几个部分而扩展。

In general, it’s impractical to memorize whether algorithms or techniques work well with multicollinearity, but it is usually true that any model that treats features the ‘same’ (makes assumptions about feature relationships) or doesn’t measure information content is vulnerable to multicollinearity.

总的来说，记住算法或技术在多重共线性中是否能很好地工作是不切实际的，但是通常确实的是，任何对待特征“相同”(对特征关系做出假设)或不测量信息内容的模型都容易受到多重共线性的影响。

What does this mean?

这是什么意思？

Take, for instance, the decision tree, which is not vulnerable to multicollinearity because it explicitly measures information content (opposite of entropy) and makes no other assumptions or measurements of relationships between features. If columns A and B are correlated with each other, the decision tree will simply choose one and discard the other (or place it very low). In this case, features are considered by their information content.

以决策树为例，该决策树不易受到多重共线性的影响，因为它显式地测量信息内容(与熵相反)，并且不进行其他假设或度量要素之间的关系。 如果A列和B列相互关联，则决策树将只选择其中一个并丢弃另一个(或将其放置得很低)。 在这种情况下，要素将通过其信息内容来考虑。

On the other hand, K-Nearest Neighbors is affected by multicollinearity because it assumes every point can be represented in multidimensional space as some coordinate (e.g. (3, 2.5, 6.7, 9.8) on an x training set with four dimensions). It doesn’t measure information content, and treats features as the same. Hence, one can imagine that data points between two highly correlated features would cluster together along a line, and how that would interfere with cross-dimensional distances.

在另一方面，K最近邻是由多重共线性，因为它假设每个点都可以在多维空间被表示为一些坐标的影响(例如(3, 2.5, 6.7, 9.8)上的x训练集具有四个尺寸)。 它不度量信息内容，并且将特征视为相同。 因此，可以想象两个高度相关的要素之间的数据点将沿着一条线聚在一起，以及如何干扰跨维距离。

Principal Component Analysis is an unsupervised method, but we can still evaluate it along these criteria! The goal of PCA is to explicitly retain the variance, or structure (information) of a reduced dataset, which is why it is not only generally immune to multicollinearity but is often used to reduce multicollinearity in datasets.

主成分分析是一种无监督的方法，但是我们仍然可以按照这些标准对其进行评估！ PCA的目标是明确保留简化数据集的方差或结构(信息)，这就是为什么它不仅通常不受多重共线性影响，而且经常用于减少数据集中的多重共线性。

Most efficient solving methods for algorithms rely on matrix mathematics and linear algebra systems — essentially representations of high-dimensional spaces, which are easily screwed with by multicollinearity.

用于算法的最有效的求解方法依赖于矩阵数学和线性代数系统-本质上是高维空间的表示，这些空间很容易被多重共线性所迷惑。

Common techniques like heavy one-hot encoding (dummy variables) in which categorical variables are represented as 0s and 1s can also be damaging because they form a perfectly linear relationship. Say that we have three binary columns A, B, and C, indicating if a row is part of one of the categories. The sum of these columns must add to 1, and hence a perfectly linear relationship A+B+C=1 is established.

诸如重一键编码(虚拟变量)之类的常用技术(其中分类变量以0和1表示)也可能是有害的，因为它们形成了完美的线性关系。 假设我们有三个二进制列A，B和C，它们指示一行是否属于类别之一。 这些列的总和必须加1，因此建立了完美的线性关系A+B+C=1 。

How can we identify multicollinearity?

我们如何识别多重共线性？

• Use a VIF (Variance Inflation Factor) score on a regression model to identify is multicollinearity is present in your dataset.
  在回归模型上使用VIF(方差通货膨胀因子)得分来确定数据集中是否存在多重共线性。
• If standard errors are too high, it may be an indicator that one error is being repeatedly propagated because of information overlap.
  如果标准错误过高，则可能表明由于信息重叠，一个错误正在重复传播。
• Large changes in parameters when adding or removing new features indicate heavily duplicated information.
  添加或删除新功能时，参数的较大变化表示信息重复很多。
• Create a correlation matrix. Features with values consistently above 0.4 are indicators of multicollinearity.
  创建一个相关矩阵。 值始终高于0.4的要素表示多重共线性。

There are many solutions to multicollinearity:

多重共线性有多种解决方案：

• Use an algorithm that is immune to multicollinearity if it is an inherent aspect of the data and other transformations are not feasible. Ridge regression, principal component regression, or partial least squares regression are all good regression alternatives.
  如果它是数据的固有方面并且其他转换不可行，则使用不受多重共线性影响的算法。 岭回归，主成分回归或偏最小二乘回归都是很好的回归选择。
• Use PCA to reduce the dimensionality of the dataset and only retain variables that are important towards preserving the data’s structure. This is beneficial if the dataset is overall very multicollinear.
  使用PCA可以减少数据集的维数，并且仅保留对于保留数据结构很重要的变量。 如果数据集总体上非常多共线性，这将是有益的。
• Use a feature selection method to remove highly correlated features.
  使用特征选择方法删除高度相关的特征。
• Obtain more data — this is the preferred method. More data can allow the model to retain the current amount of information while giving context and perspective to noise.
  获取更多数据-这是首选方法。 更多数据可以使模型保留当前的信息量，同时为噪声提供上下文和透视图。