主成份分析算法PCA
非监督学习算法
PCA的实现:
简单来说,就是将数据从原始的空间中转换到新的特征空间中,例如原始的空间是三维的(x,y,z),x、y、z分别是原始空间的三个基,我们可以通过某种方法,用新的坐标系(a,b,c)来表示原始的数据,那么a、b、c就是新的基,它们组成新的特征空间。在新的特征空间中,可能所有的数据在c上的投影都接近于0,即可以忽略,那么我们就可以直接用(a,b)来表示数据,这样数据就从三维的(x,y,z)降到了二维的(a,b)。
问题是如何求新的基(a,b,c)?
一般步骤是这样的:
对原始数据零均值化(中心化),
求协方差矩阵,
对协方差矩阵求特征向量和特征值,这些特征向量组成了新的特征空间。
PCA–零均值化(中心化):
中心化即是指变量减去它的均值,使均值为0。
其实就是一个平移的过程,平移后使得所有数据的中心点是(0,0)
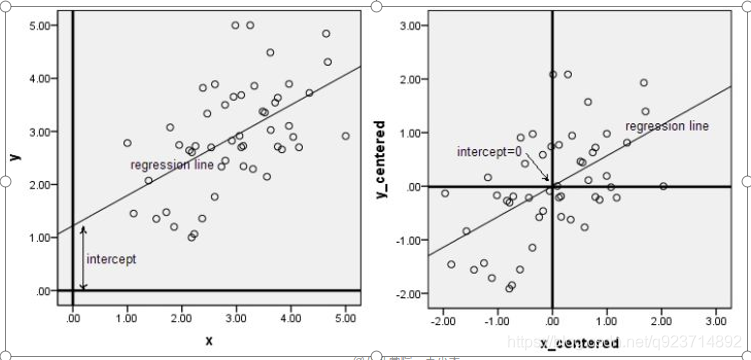
只有中心化数据之后,计算得到的方向才能比较好的“概括”原来的数据。
此图形象的表述了,中心化的几何意义,就是将样本集的中心平移到坐标系的原点O上。

PCA–PCA降维的几何意义:
我们对于一组数据,如果它在某一坐标轴上的方差越大,说明坐标点越分散,该属性能够比较好的反映源数据。所以在进行降维的时候,主要目的是找到一个超平面,它能使得数据点的分布方差呈最大,这样数据表现在新的坐标轴上时候已经足够分散了。
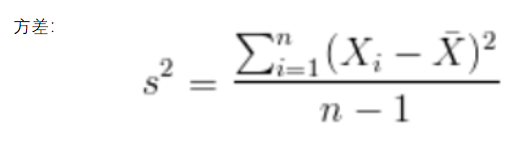
PCA算法的优化目标就是:
① 降维后同一维度的方差最大 ② 不同维度之间的相关性为0(协方差)
PCA–协方差矩阵:
定义:

比如,三维(x,y,z)的协方差矩阵: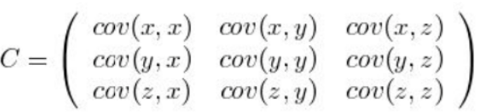
协方差矩阵的特点:
协方差矩阵计算的是不同 维度之间的协方差, 而不是不同样本之间的。
样本矩阵的每行是一个样本, 每列为一个维度, 所以我们要按列计算均值。
协方差矩阵的对角线就是各个维度上的方差
特别的,如果做了中心化,则协方差矩阵为(中心化矩阵的协方差矩阵公式):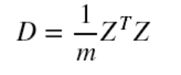
PCA–对特征值进行排序:

PCA–评价模型的好坏,K值的确定
通过特征值的计算我们可以得到主成分所占的百分比,用来衡量模型的好坏。
对于前k个特征值所保留下的信息量计算方法如下:
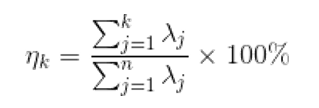
代码实现:
手动实现:
import numpy as np
class PCA():def __init__(self,n_components):self.n_components = n_componentsdef fit_transform(self,X):self.n_features_ = X.shape[1]# 求协方差矩阵X = X - X.mean(axis=0) #0均值化self.covariance = np.dot(X.T,X)/X.shape[0] #求协方差# 求协方差矩阵的特征值和特征向量eig_vals,eig_vectors = np.linalg.eig(self.covariance)# 获得降序排列特征值的序号idx = np.argsort(-eig_vals)# 降维矩阵self.components_ = eig_vectors[:,idx[:self.n_components]]# 对X进行降维return np.dot(X,self.components_)# 调用
pca = PCA(n_components=2) #降维为2
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]]) #导入数据,维度为4
newX=pca.fit_transform(X)
print(newX) #输出降维后的数据结果展示:
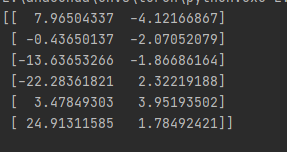
接口实现:
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]]) #导入数据,维度为4
pca = PCA(n_components=2) #降到2维
pca.fit(X) #训练
newX=pca.fit_transform(X) #降维后的数据
# PCA(copy=True, n_components=2, whiten=False)
print(pca.explained_variance_ratio_) #输出贡献率
print(newX) #输出降维后的数据结果展示:
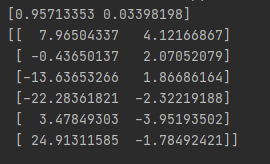
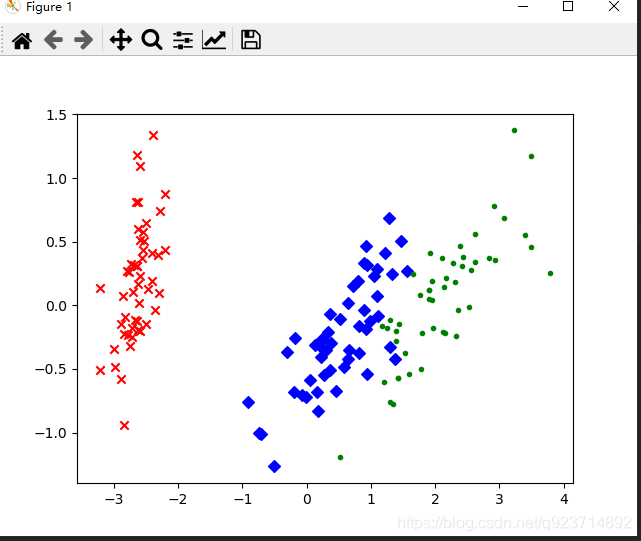
PCA–鸢尾花实例:
我们通过Python的sklearn库来实现鸢尾花数据进行降维,数据本身是4维的降维后变成2维。
其中样本总数为150,鸢尾花的类别有三种。
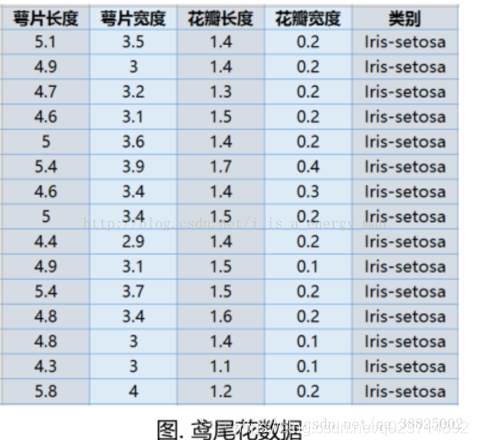
代码实现:
import matplotlib.pyplot as plt
import sklearn.decomposition as dp
from sklearn.datasets import load_irisx,y=load_iris(return_X_y=True) #加载数据,x表示数据集中的属性数据,y表示数据标签
pca=dp.PCA(n_components=2) #加载pca算法,设置降维后主成分数目为2
reduced_x=pca.fit_transform(x) #对原始数据进行降维,保存在reduced_x中
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]
for i in range(len(reduced_x)): #按鸢尾花的类别将降维后的数据点保存在不同的表中if y[i]==0:red_x.append(reduced_x[i][0])red_y.append(reduced_x[i][1])elif y[i]==1:blue_x.append(reduced_x[i][0])blue_y.append(reduced_x[i][1])else:green_x.append(reduced_x[i][0])green_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()结果展示:
PCA算法的优缺点:
优点:
它是无监督学习,完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预,最后的结果只与数据相关,与用户是独立的。
用PCA技术可以对数据进行降维,同时对新求出的“主元”向量的重要性进行排序,根据需要取前面最重要的部分,将后面的维数省去,可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。
各主成分之间正交,可消除原始数据成分间的相互影响。
计算方法简单,易于在计算机上实现。
缺点:
如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高。
贡献率小的主成分往往可能含有对样本差异的重要信息。
特征值矩阵的正交向量空间是否唯一有待讨论。
在非高斯分布的情况下,PCA方法得出的主元可能并不是最优的,此时在寻找主元时不能将方差作为衡量重要性的标准。














DDL增强功能-数据类型、同义词、分区表)

初衷、感想与笔记目录)


