1 CDF
累积分布函数(Cumulative Distribution Function,CDF),又叫分布函数,是概率密度函数的积分,能完整描述一个实随机变量X的概率分布。一般以大写CDF标记,,与概率密度函数probability density function(小写pdf)相对。
对于所有实数 ,累积分布函数定义如下:
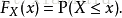
即累积分布函数表示:对离散变量而言,所有小于等于a的值出现概率的和。
2 CCDF
互补累计分布函数(Complementary Cumulative Distribution Function,CCDF) 为了表示OFDM系统中的峰均值PAPR的统计特性所引入的的概念,它定义为多载波传输系统中峰均值超过某一门限值z的概率。互补累积分布函数是对连续函数,所有大于a的值,其出现概率的和。
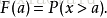
3 用CDF计算期望

https://blog.csdn.net/xiaofalu/article/details/81667337
https://blog.csdn.net/itnerd/article/details/85545524






方法)

流和会话)










