在强化学习中,马尔科夫决策过程(Markov decision process, MDP)是对完全可观测的环境进行描述的,也就是说观测到的状态内容完整地决定了决策的需要的特征。几乎所有的强化学习问题都可以转化为MDP。本讲是理解强化学习问题的理论基础。
1. 马尔科夫过程 Markov Process
1.1 马尔科夫性 Markov Property
某一状态信息包含了所有相关的历史,只要当前状态可知,所有的历史信息都不再需要,当前状态就可以决定未来,则认为该状态具有马尔科夫性。
可以用下面的状态转移概率公式来描述马尔科夫性:
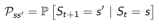
下面状态转移矩阵定义了所有状态的转移概率:
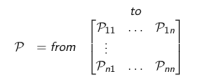
式中n为状态数量,矩阵中每一行元素之和为1.
1.2 马尔科夫过程 Markov Property
马尔科夫过程 又叫马尔科夫链(Markov Chain),它是一个无记忆的随机过程,可以用一个元组<S,P>表示,其中S是有限数量的状态集,P是状态转移概率矩阵。
1.3 示例——学生马尔科夫链
本讲多次使用了学生马尔科夫链这个例子来讲解相关概念和计算。
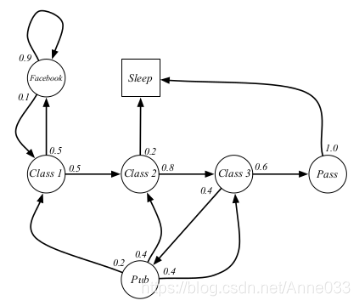
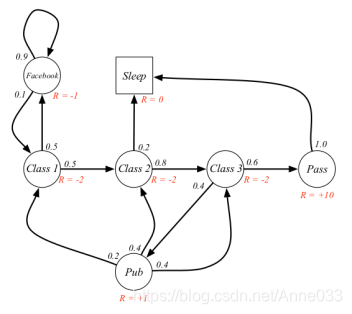
图中,圆圈表示学生所处的状态,方格Sleep是一个终止状态,或者可以描述成自循环的状态,也就是Sleep状态的下一个状态100%的几率还是自己。箭头表示状态之间的转移,箭头上的数字表示当前转移的概率。
举例说明:当学生处在第一节课(Class1)时,他/她有50%的几率会参加第2节课(Class2);同时在也有50%的几率不在认真听课,进入到浏览facebook这个状态中。在浏览facebook这个状态时,他/她有90%的几率在下一时刻继续浏览,也有10%的几率返回到课堂内容上来。当学生进入到第二节课(Class2)时,会有80%的几率继续参加第三节课(Class3),也有20%的几率觉得课程较难而退出(Sleep)。当学生处于第三节课这个状态时,他有60%的几率通过考试,继而100%的退出该课程,也有40%的可能性需要到去图书馆之类寻找参考文献,此后根据其对课堂内容的理解程度,又分别有20%、40%、40%的几率返回值第一、二、三节课重新继续学习。一个可能的学生马尔科夫链从状态Class1开始,最终结束于Sleep,其间的过程根据状态转化图可以有很多种可能性,这些都称为Sample Episodes。以下四个Episodes都是可能的:
C1 - C2 - C3 - Pass - Sleep
C1 - FB - FB - C1 - C2 - Sleep
C1 - C2 - C3 - Pub - C2 - C3 - Pass - Sleep
C1 - FB - FB - C1 - C2 - C3 - Pub - C1 - FB - FB - FB - C1 - C2 - C3 - Pub - C2 - Sleep
该学生马尔科夫过程的状态转移矩阵如下图:
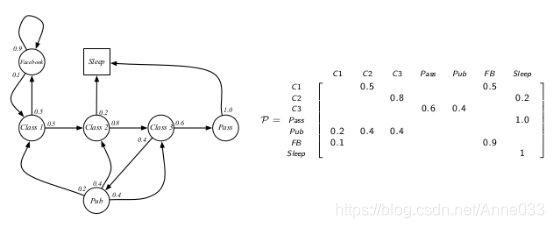
2 马尔科夫奖励过程 Markov Reward Process
马尔科夫奖励过程在马尔科夫过程的基础上增加了奖励R和衰减系数γ:<S,P,R,γ>。R是一个奖励函数。S状态下的奖励是某一时刻(t)处在状态s下在下一个时刻(t+1)能获得的奖励期望:
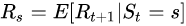
很多听众纠结为什么奖励是t+1时刻的。照此理解起来相当于离开这个状态才能获得奖励而不是进入这个状态即获得奖励。David指出这仅是一个约定,为了在描述RL问题中涉及到的观测O、行为A、和奖励R时比较方便。他同时指出如果把奖励改为 [公式] 而不是 [公式] ,只要规定好,本质上意义是相同的,在表述上可以把奖励描述为“当进入某个状态会获得相应的奖励”。
衰减系数 Discount Factor: γ∈ [0, 1],它的引入有很多理由,其中优达学城的“机器学习-强化学习”课程对其进行了非常有趣的数学解释。David也列举了不少原因来解释为什么引入衰减系数,其中有数学表达的方便,避免陷入无限循环,远期利益具有一定的不确定性,符合人类对于眼前利益的追求,符合金融学上获得的利益能够产生新的利益因而更有价值等等。
下图是一个“马尔科夫奖励过程”图示的例子,在“马尔科夫过程”基础上增加了针对每一个状态的奖励,由于不涉及衰减系数相关的计算,这张图并没有特殊交代衰减系数值的大小。
2.1 收获 Return
定义:收获GtG_tGt为在一个马尔科夫奖励链上从t时刻开始往后所有的奖励的有衰减的总和。也有翻译成“收益”或"回报"。公式如下:
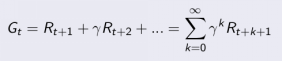
其中衰减系数体现了未来的奖励在当前时刻的价值比例,在k+1时刻获得的奖励R在t时刻的体现出的价值是γkR\gamma^k RγkR,γ接近0,则表明趋向于“近视”性评估;γ接近1则表明偏重考虑远期的利益。
2.2 价值函数 Value Function
价值函数给出了某一状态或某一行为的长期价值。
定义:一个马尔科夫奖励过程中某一状态的价值函数为从该状态开始的马尔可夫链收获的期望:
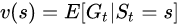
注:价值可以仅描述状态,也可以描述某一状态下的某个行为,在一些特殊情况下还可以仅描述某个行为。在整个视频公开课中,除了特别指出,约定用状态价值函数或价值函数来描述针对状态的价值;用行为价值函数来描述某一状态下执行某一行为的价值,严格意义上说行为价值函数是“状态行为对”价值函数的简写。
2.3 举例说明收获和价值的计算
为方便计算,把“学生马尔科夫奖励过程”示例图表示成下表的形式。表中第二行对应各状态的即时奖励值,蓝色区域数字为状态转移概率,表示为从所在行状态转移到所在列状态的概率:
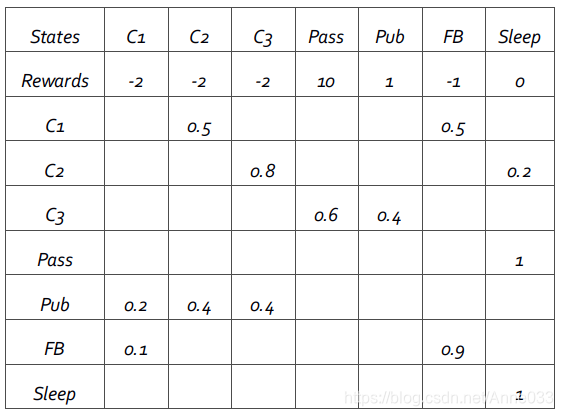
考虑如下4个马尔科夫链。现计算当γ= 1/2时,在t=1时刻(S1=C1S_1=C_1S1=C1 )时状态S1S_1S1 的收获分别为:

从上表也可以理解到,收获是针对一个马尔科夫链中的某一个状态来说的。
当γ= 0时,上表描述的MRP中,各状态的即时奖励就与该状态的价值相同。当γ≠ 0时,各状态的价值需要通过计算得到,这里先给出γ分别为0, 0.9,和1三种情况下各状态的价值,如下图所示。
各状态圈内的数字表示该状态的价值,圈外的R=-2等表示的是该状态的即时奖励。
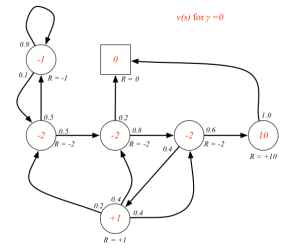
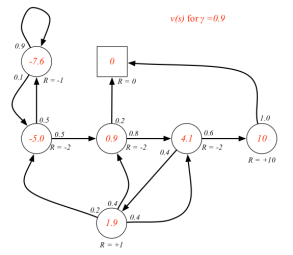
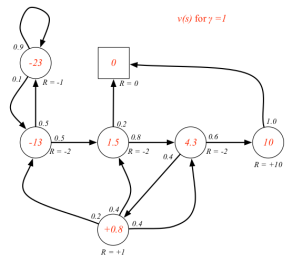
各状态价值的确定是很重要的,RL的许多问题可以归结为求状态的价值问题。因此如何求解各状态的价值,也就是寻找一个价值函数(从状态到价值的映射)就变得很重要了。
2.4 价值函数的推导
2.4.1 Bellman方程 - MRP
先尝试用价值的定义公式来推导看看能得到什么:
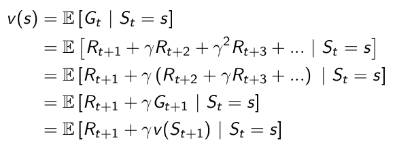
这个推导过程相对简单,仅在导出最后一行时,将Gt+1G_{t+1}Gt+1变成了v(St+1)v(S_{t+1})v(St+1)。其理由是收获的期望等于收获的期望的期望。下式是针对MRP的Bellman方程:
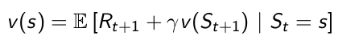
通过方程可以看出 [公式] 由两部分组成,一是该状态的即时奖励期望,即时奖励期望等于即时奖励,因为根据即时奖励的定义,它与下一个状态无关;另一个是下一时刻状态的价值期望,可以根据下一时刻状态的概率分布得到其期望。如果用s’表示s状态下一时刻任一可能的状态,那么Bellman方程可以写成:
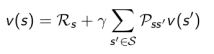
2.4.2 方程的解释
下图已经给出了γ=1时各状态的价值(该图没有文字说明γ=1,根据视频讲解和前面图示以及状态方程的要求,γ必须要确定才能计算),状态 [公式] 的价值可以通过状态Pub和Pass的价值以及他们之间的状态转移概率来计算:
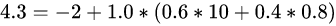
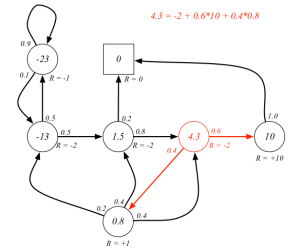
2.4.3 Bellman方程的矩阵形式和求解

大规模MRP的求解通常使用迭代法。常用的迭代方法有:动态规划Dynamic Programming、蒙特卡洛评估Monte-Carlo evaluation、时序差分学习Temporal-Difference,后文会逐步讲解这些方法。
3 马尔科夫决定过程 Markov Decision Process
相较于马尔科夫奖励过程,马尔科夫决定过程多了一个行为集合A,它是这样的一个元组: <S, A, P, R, γ>。看起来很类似马尔科夫奖励过程,但这里的P和R都与具体的行为a对应,而不像马尔科夫奖励过程那样仅对应于某个状态,A表示的是有限的行为的集合。具体的数学表达式如下:

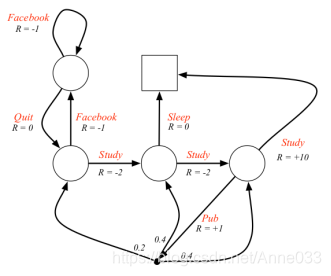
3.1 示例——学生MDP
下图给出了一个可能的MDP的状态转化图。图中红色的文字表示的是采取的行为,而不是先前的状态名。对比之前的学生MRP示例可以发现,即时奖励与行为对应了,同一个状态下采取不同的行为得到的即时奖励是不一样的。由于引入了Action,容易与状态名混淆,因此此图没有给出各状态的名称;此图还把Pass和Sleep状态合并成一个终止状态;另外当选择”去查阅文献”这个动作时,主动进入了一个临时状态(图中用黑色小实点表示),随后被动的被环境按照其动力学分配到另外三个状态,也就是说此时Agent没有选择权决定去哪一个状态。
3.2 策略Policy

用文字描述是这样的,在执行策略 [公式] 时,状态从s转移至 s’ 的概率等于一系列概率的和,这一系列概率指的是在执行当前策略时,执行某一个行为的概率与该行为能使状态从s转移至s’的概率的乘积。
3.3 奖励函数
奖励函数表示如下:
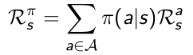
用文字表述是这样的:当前状态s下执行某一指定策略得到的即时奖励是该策略下所有可能行为得到的奖励与该行为发生的概率的乘积的和。
策略在MDP中的作用相当于agent可以在某一个状态时做出选择,进而有形成各种马尔科夫过程的可能,而且基于策略产生的每一个马尔科夫过程是一个马尔科夫奖励过程,各过程之间的差别是不同的选择产生了不同的后续状态以及对应的不同的奖励。
3.4 基于策略π的价值函数

下图用例子解释了行为价值函数
3.5 Bellman期望方程 Bellman Expectation Equation
MDP下的状态价值函数和行为价值函数与MRP下的价值函数类似,可以改用下一时刻状态价值函数或行为价值函数来表达,具体方程如下:
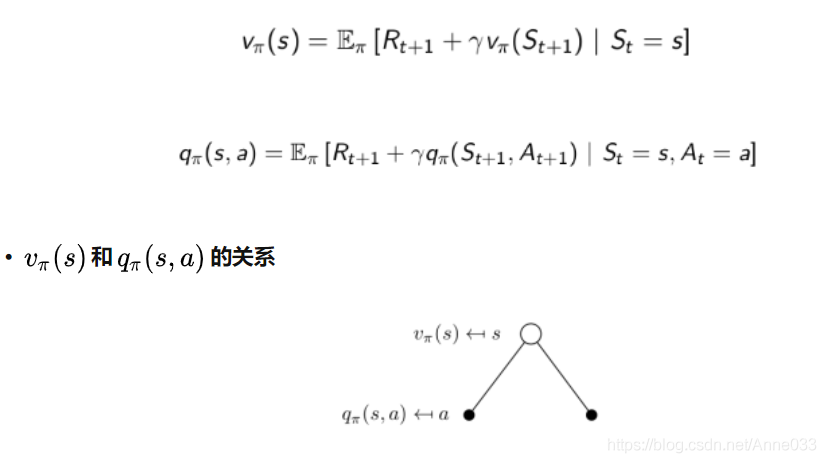
上图中,空心较大圆圈表示状态,黑色实心小圆表示的是动作本身,连接状态和动作的线条仅仅把该状态以及该状态下可以采取的行为关联起来。可以看出,在遵循策略π时,状态s的价值体现为在该状态下遵循某一策略而采取所有可能行为的价值按行为发生概率的乘积求和。

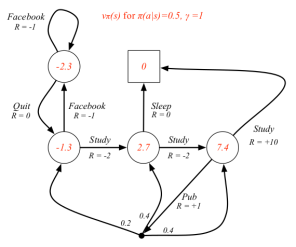
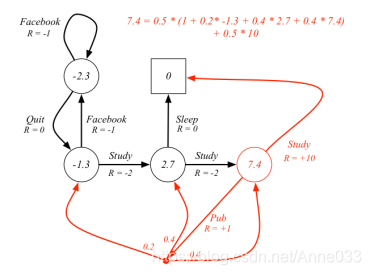
3.6 学生MDP示例
下图解释了红色空心圆圈状态的状态价值是如何计算的,遵循的策略随机策略,即所有可能的行为有相同的几率被选择执行。
3.7 Bellman期望方程矩阵形式
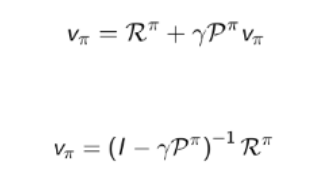
3.8 最优价值函数

最优价值函数明确了MDP的最优可能表现,当我们知道了最优价值函数,也就知道了每个状态的最优价值,这时便认为这个MDP获得了解决。
学生MDP问题的最优状态价值
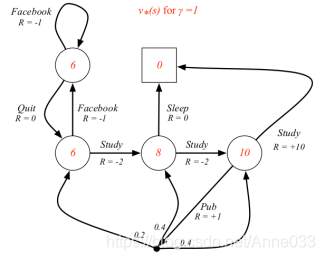
学生MDP问题的最优行为价值
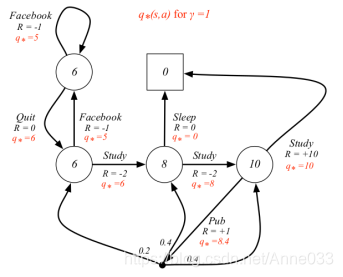
注:youtube留言认为Pub行为对应的价值是+9.4而不是+8.4
3.9 最优策略
当对于任何状态 s,遵循策略π的价值不小于遵循策略 π’ 下的价值,则策略π优于策略 π’:
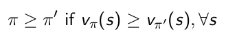
定理 对于任何MDP,下面几点成立:1.存在一个最优策略,比任何其他策略更好或至少相等;2.所有的最优策略有相同的最优价值函数;3.所有的最优策略具有相同的行为价值函数。
3.9.1 寻找最优策略
可以通过最大化最优行为价值函数来找到最优策略:
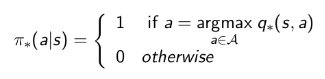
对于任何MDP问题,总存在一个确定性的最优策略;同时如果我们知道最优行为价值函数,则表明我们找到了最优策略。
3.9.2 学生MDP最优策略示例
红色箭头表示的行为表示最优策略
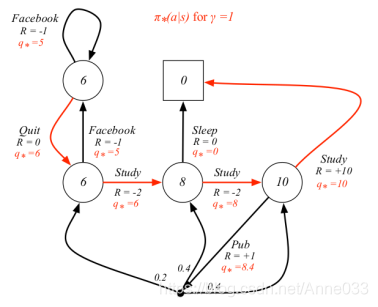
3.10 Bellman最优方程 Bellman Optimality Equation
针对 [公式] ,一个状态的最优价值等于从该状态出发采取的所有行为产生的行为价值中最大的那个行为价值:
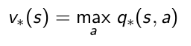
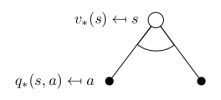
针对q∗q_*q∗ ,在某个状态s下,采取某个行为的最优价值由2部分组成,一部分是离开状态 s 的即刻奖励,另一部分则是所有能到达的状态 s’ 的最优状态价值按出现概率求和:
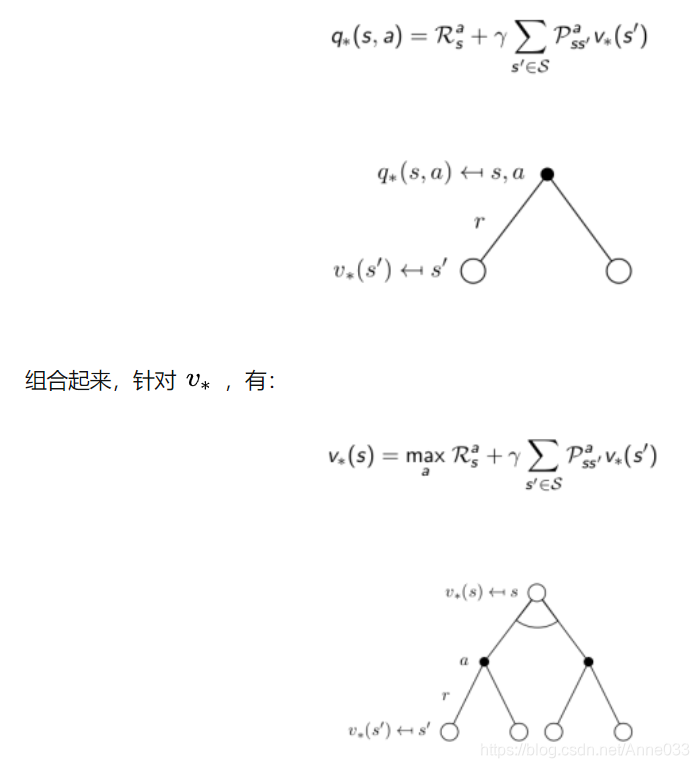
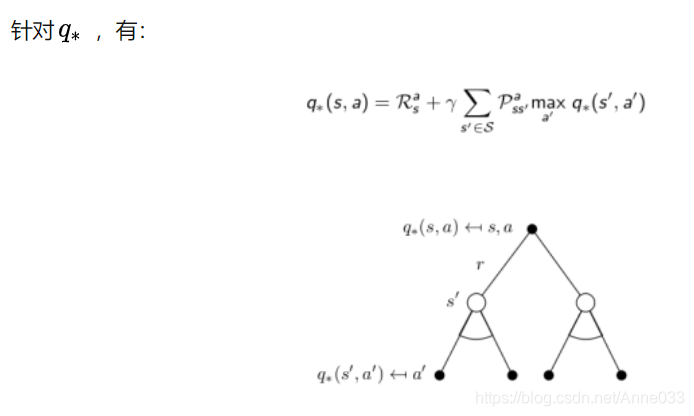
3.11 Bellman最优方程学生MDP示例
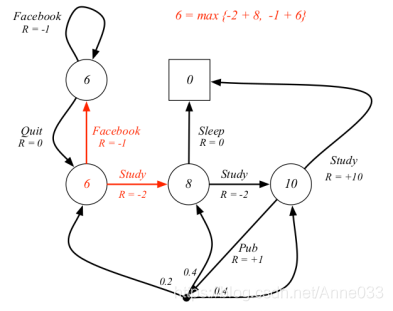
3.12 求解Bellman最优方程
Bellman最优方程是非线性的,没有固定的解决方案,通过一些迭代方法来解决:价值迭代、策略迭代、Q学习、Sarsa等。后续会逐步讲解展开。
4 MDP延伸——Extensions to MDPs
简要提及:无限状态或连续MDP;部分可观测MDP;非衰减、平均奖励MDP
https://zhuanlan.zhihu.com/p/28084942


方法)

流和会话)












)
)
)