图像处理作业
1
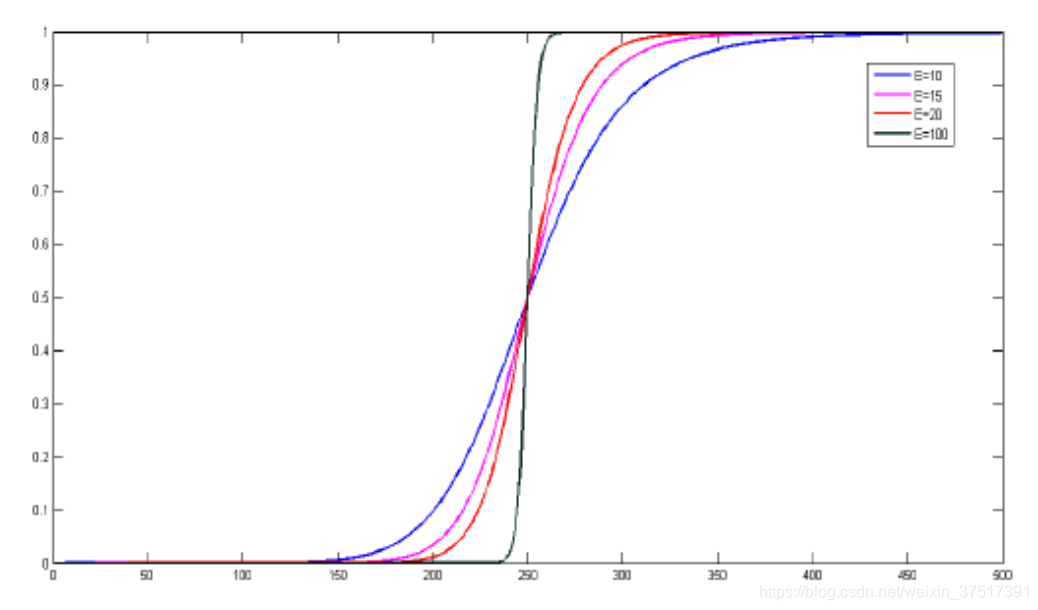
取s=T(r)=11+(mr)Es=T(r)=\frac{1}{1+(\frac{m}{r})^E}s=T(r)=1+(rm)E1
其中rrr为原始亮度,mmm为输入区间的中点,EEE描述曲线的陡峭程度
2
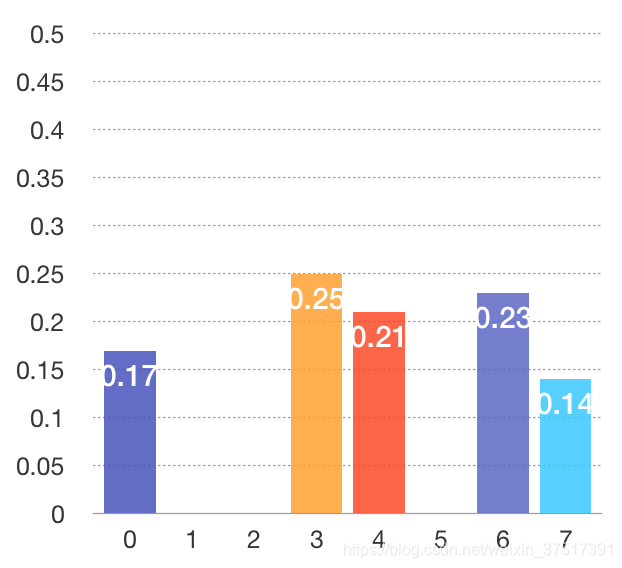
一幅8灰度级图像具有如下所示的直方图,求直方图均衡后的灰度级和对应概率,并画出均衡后的直方图的示意图。(图中的8个不同灰度级对应的归一化直方图为[0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02])
s0=7∑j=00p(rj)=1.19s_0 = 7\sum_{j=0}^{0}p(r_j)=1.19s0=7∑j=00p(rj)=1.19
s1=7∑j=01p(rj)=2.94s_1 = 7\sum_{j=0}^{1}p(r_j)=2.94s1=7∑j=01p(rj)=2.94
s2=7∑j=02p(rj)=4.41s_2 = 7\sum_{j=0}^{2}p(r_j)=4.41s2=7∑j=02p(rj)=4.41
s3=7∑j=03p(rj)=5.53s_3 = 7\sum_{j=0}^{3}p(r_j)=5.53s3=7∑j=03p(rj)=5.53
s4=7∑j=04p(rj)=6.02s_4 = 7\sum_{j=0}^{4}p(r_j)=6.02s4=7∑j=04p(rj)=6.02
s5=7∑j=05p(rj)=6.58s_5 = 7\sum_{j=0}^{5}p(r_j)=6.58s5=7∑j=05p(rj)=6.58
s6=7∑j=06p(rj)=6.68s_6 = 7\sum_{j=0}^{6}p(r_j)=6.68s6=7∑j=06p(rj)=6.68
s7=7∑j=07p(rj)=7.00s_7 = 7\sum_{j=0}^{7}p(r_j)=7.00s7=7∑j=07p(rj)=7.00
将其四舍五入到最接近的整数中去:
s0=1,s1=3,s2=4,s3=6,s4=6,s5=7,s6=7,s7=7s_0=1,s_1 = 3,s_2=4,s_3=6,s_4 = 6,s_5=7,s_6=7,s_7=7s0=1,s1=3,s2=4,s3=6,s4=6,s5=7,s6=7,s7=7
均衡后的直方图如下图所示。
3
(选做题)课本习题3.6。对于离散的情况,用matlab进行一下实验。
对于连续的情况,直方图均衡公式如下
s=∫0rpr(x)dxs = \int_0^rp_r(x)dxs=∫0rpr(x)dx
可知
dsdr=pr(r)\frac{ds}{dr}=p_r(r)drds=pr(r)
ps(s)=pr(r)∗1pr(r)=1p_s(s)=p_r(r)*\frac{1}{p_r(r)}=1ps(s)=pr(r)∗pr(r)1=1
再次做直方图均衡时
pz(z)=ps(s)=1p_z(z)=p_s(s)=1pz(z)=ps(s)=1
z=∫0sps(x)dx=sz=\int_0^sp_s(x)dx=sz=∫0sps(x)dx=s
因此,再次做直方图均衡之后,不会发生改变。
离散的情况下:

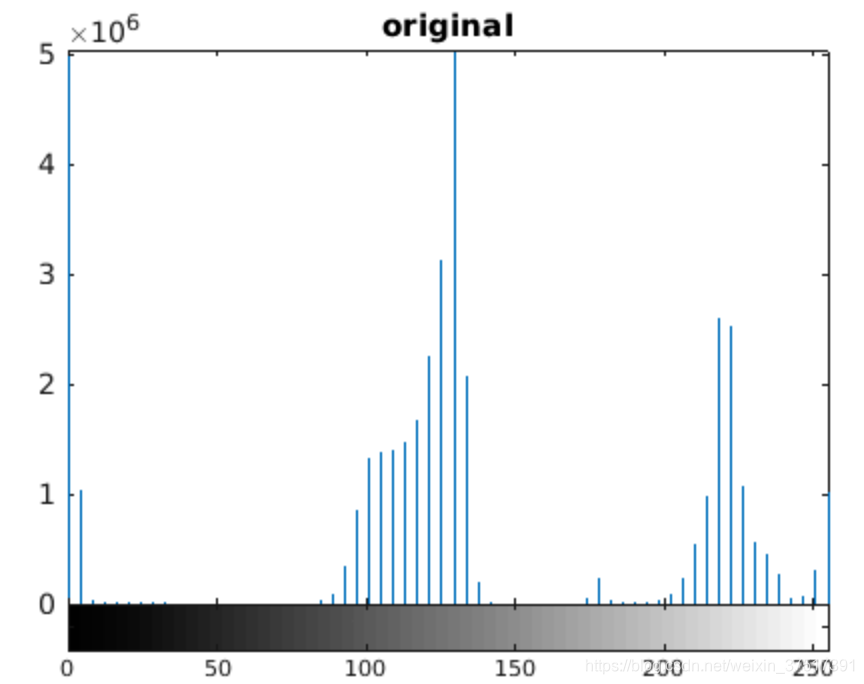
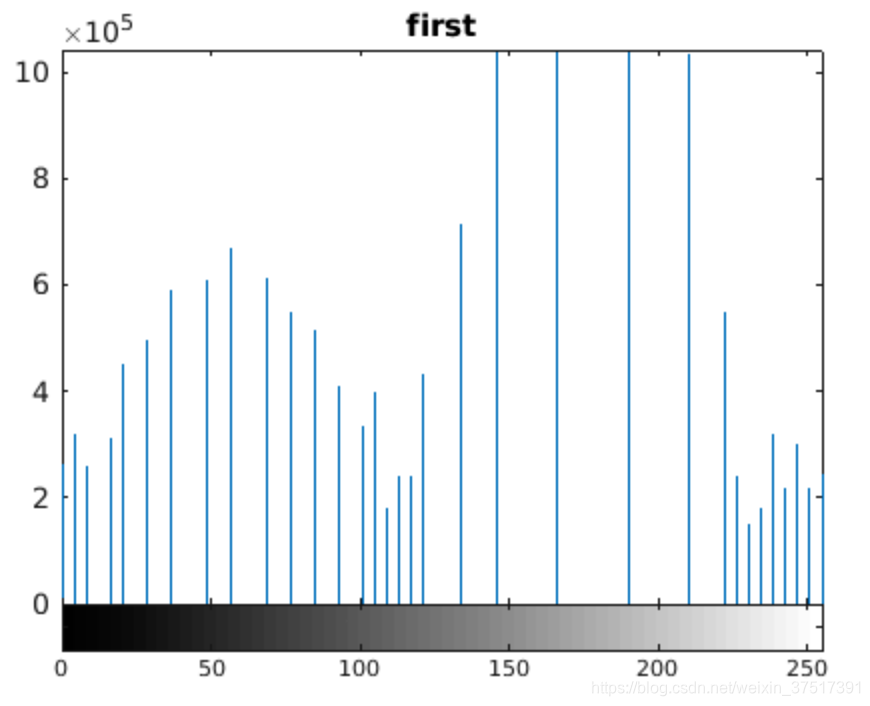
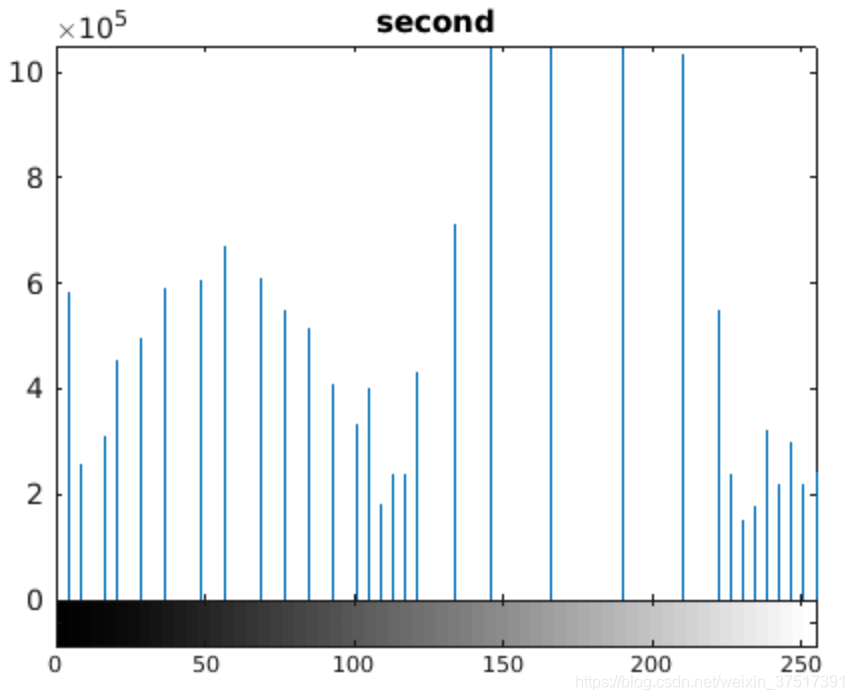
4
完成课本数字图像处理第二版114页,习题3.10。
∫0T(r)pz(x)dx=∫0rpr(x)dx\int_0^{T(r)} p_z(x)dx=\int_0^rp_r(x)dx∫0T(r)pz(x)dx=∫0rpr(x)dx
由于pz(x)=2∗x,pr(x)=2−2∗xp_z(x)=2*x,p_r(x)=2-2*xpz(x)=2∗x,pr(x)=2−2∗x
∫0T(r)pz(x)dx=∫0rpr(x)dx=∫0T(r)2xdx=∫0r2−2xdx\int_0^{T(r)} p_z(x)dx=\int_0^rp_r(x)dx=\int_0^{T(r)}2xdx=\int_0^r2-2xdx∫0T(r)pz(x)dx=∫0rpr(x)dx=∫0T(r)2xdx=∫0r2−2xdx
(T(r))2=2r−r2(T(r))^2=2r-r^2(T(r))2=2r−r2
T(r)=2r−r2T(r)=\sqrt {2r-r^2}T(r)=2r−r2

.NET技术交流会圆满成功)
![P5322-[BJOI2019]排兵布阵【背包】](http://pic.xiahunao.cn/P5322-[BJOI2019]排兵布阵【背包】)



![P5268-[SNOI2017]一个简单的询问【莫队】](http://pic.xiahunao.cn/P5268-[SNOI2017]一个简单的询问【莫队】)

)

![P3850-[TJOI2007]书架【Splay】](http://pic.xiahunao.cn/P3850-[TJOI2007]书架【Splay】)
)



)
![P5304-[GXOI/GZOI2019]旅行者【最短路】](http://pic.xiahunao.cn/P5304-[GXOI/GZOI2019]旅行者【最短路】)


)