0、目录

---

 整体架构目录：ASP.NET Core分布式项目实战-目录

 

一、微服务选型

---

在做微服务架构的技术选型的时候，以“无侵入”和“社区活跃”为主要的考量点，将来升级为原子服务架构、量子服务架构的时候、甚至恢复成单体架构的时候，代价最小。

软件开发只需要组装，不再需要从头开发。

选型可以参考一下张队长的文章： 微软MVP张善友告诉你，微服务选型要注意这些地方

二、微服务架构是什么？

---

 

每一个微服务都是一个零件，并使用这些零件组装出不同的形状。微服务架构就是把一个大系统按业务功能分解成多个职责单一的小系统，并利用简单的方法使多个小系统相互协作，组合成一个大系统。
服务之间互相协调、互相配合，为用户提供最终价值，每个服务运行在其独立的进程中，服务于服务间采用轻量级的通信机制互相协作，通常是基于HTTP协议的RESTful API或者RPC。
核心思想：把大系统拆分为小系统。

三、微服务组件

---

服务注册：服务提供方将自己调用地址注册到服务注册中心，让服务调用方能够方便地找到自己。

服务发现：服务调用方从服务注册中心找到自己需要调用的服务的地址。
负载均衡:
服务网关：服务网关是服务调用的唯一入口。
配置中心:
API管理：
集成框架：微服务组件都以职责单一的程序包对外提供服务，集成框架以配置的形式将所有微服务组件（特别是管理端组件）集成到统一的界面框架下，让用户能够在统一的界面中使用系统。 
分布式事务：保证数据的一致性
调用链 ：记录完成一个业务逻辑时调用到的微服务，并将这种串 行或并行的调用关系展示出来。在系统出错时，可以方便地找到 出错点。 （监控）
支撑平台：由于微服务化后，系统变得更加碎片化，系统的部署、运维、监控等都比单体架构更加复杂，就需要用到自动化.

四、微服务架构优势？为什么要采用微服务架构？

---

 

微服务与单体的比较，可看下图：

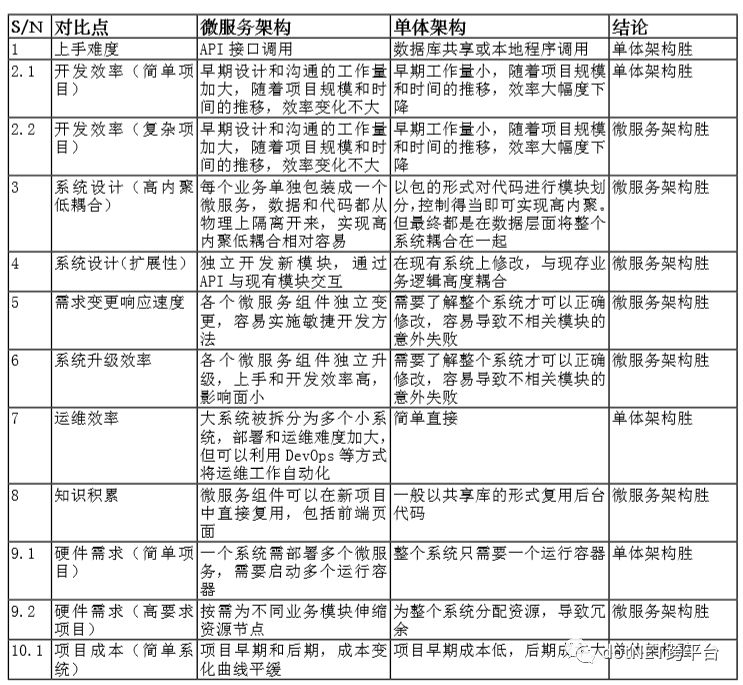
什么时候选用微服务呢？

从个人来看，有三种场景可以考虑使用微服务
1、规模大 ，团队超过10人
2、业务复杂度高，系统超过5个子模块
3、需要长期演进，项目开发和维护周期超过半年

 

五、快速体验微服务架构

---

 

使用微服务简单模式进行开发的四个步骤：
1、沿用组织中现有的技术体系开发单一职责的微服务
2、服务提供方将地址信息注册到注册中心，调用方将服务地址从注册中心拉下来。
3、通过门户后端（服务网关）将服务API暴露给门户和移动APP。
4、将管理端模块集成到统一的操作界面上。

 

六、运维

---

 

基础设施：自动构建、自动部署、日志中心、健康 检查、性能监控等功能
gitlab-CI/CD、Jenkins+gitlab-CI/CD：自动化部署
K8s&Docker+Jenkins&Pipeline+Gitlab--CI/CD：自动化部署
ELK:日志
zipkin/skywalking：微服务监控

七、总结

---

 

我们只需要在开发 层面理解了注册中心、服务发现、负载均衡、服务网关和管理端集成框架， 在运维层面准备好持续集成工具、配置中心和监控告警工具，就可以很容 易地落地微服务架构，享受微服务架构带来的精彩。祝大家玩得愉快。

  

八、微服务架构API的开发与治理

---

 

1、开放给互联网用户调用的API需要在API网关上加上授权、鉴权、限流、限并发、统计、计费等功能

2、内网环境：提供给内网里的其他微服务调用的API。

1、内网环境API开发

---

 

1、需要先考虑是用HTTP API还是RPC？

HTTP API：
指的是简单的基于HTTP协议的API，具体的例子就是MVC的Controller,
http://127.0.0.1/helloworld

RPC:
远程过程调用(大多数指Socker通信方法的远程调用)，也可以使用HTTP协议来实现RPC调用，例如gRPC.

HTTP 简单、RPC基于Socket的RPC性能更好。但我最后还是选择了HTTP API来使用。

2、HTTP API 的性能足以支撑多数项目

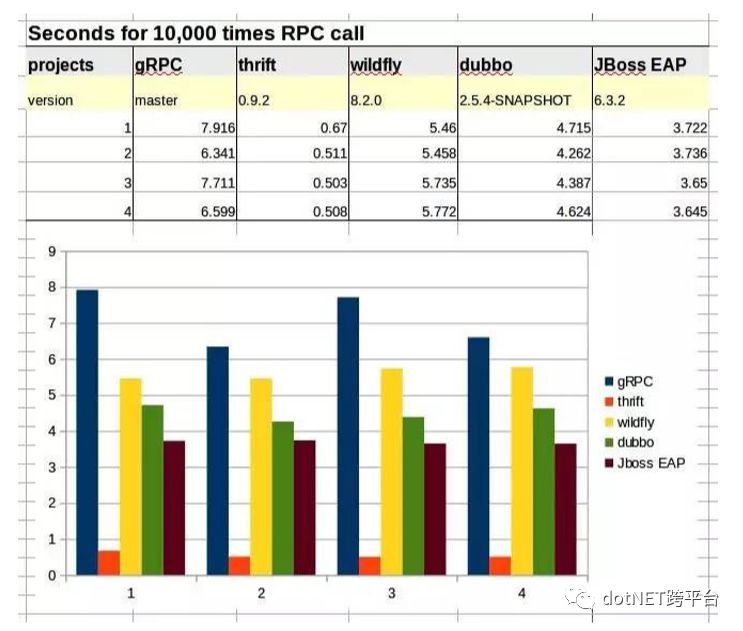
RPC的协议吞吐量是HTTP性能的几倍，如 protobuf、Thrift、Kyro、Dubbo
等，在考虑自身技术栈、成本、稳定性、易用性、可维护性、业务场景等因素考虑，HTT和RPC的性能差别并不是主要问题。

 

 

九、如何保障微服务架构下的数据一致性

---

 

以电商平台为例，当用户下单并支付后，系统需要修改订单的状态并
且增加用户积分。由于系统采用的是微服务架构，分离出了支付服务、订 单服务和积分服务，每个服务都有独立数据库做数据存储。当用户支付成 功后，无论是修改订单状态失败还是增加积分失败，都会 造成数据的不 一致。

 

然而微服务架构下，每个微服务都有自己的数据库，导致微服务架构 的系统不能简单地满足 ACID，我们就需要寻找微服务架构下的数据一致性解决方案：

CAP是指在一个分布式系统下，包含三个要素：：Consistency（一致性）、 Availability（可用性）、Partition tolerance（分区容错性），并且 三者不 可得兼。 
C:所有数据变动都是同步的
A：即在可以接受的时间范围内正确的相应用户请求
P：分区容错性，即某节点或网络分区故障时，系统仍能提供满足一致性和可用性的服务。
在分布式系统下，为了保证模块的分区容错性，只能在数据强一致性和可用性之间做平衡。具体表现为在一定时间内，可能模块之间数据是不一致的，但是通过自动或者手动补偿后能够达到最终的一致。

分享我们是如何保证微服务架构的数据一致性的：

1、可靠消息最终一致性（适用于跨平台技术栈不统一的场景）

利用MQ组件实现的二阶段提交，涉及三个模块：
A、上游应用，执行业务并发送MQ消息
B、可靠消息服务和MQ消息组件，协调上下游消息的传递，并确保上下游数据的一致性。
C、下游应用，监听MQ的消息并执行自身业务。

2、TCC方案

涉及三个模块：主业务、从业务、活动管理器
1、主业务服务分别调用所有从业务服务的try操作，并在活动管理器中记录所有从业务服务。当所有从业服务try成功或者某个从业服务try失败时，进入第二阶段。
2、活动管理器根据第一阶段从业服务的try结果来执行confirm或cancel操作。如果第一阶段所有从业务服务都try成功，则协作者调用所有从业服务的confirm操作，否则，调用所有从业务服务的cancel操作。
Confirm 失败：则回滚所有 confirm 操作并执行 cancel 操作。 
Cancel 失败：从业务服务需要提供自动 cancel 机制，以保证 cancel 成功。

 参考地址：

张队长文章： 微软MVP张善友告诉你，微服务选型要注意这些地方

原文地址: https://www.cnblogs.com/guolianyu/p/9568400.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com