背景
产品在新功能发布前，可能会采取小流量测试的方式，或者在确定方案前使用A/B测试来衡量。一般开发人员会跟运维同学合作，通过一些现有平台切换机器或者流量来实现。本文介绍了另外一种简便的方式，并解释了其在持续集成上的应用，同时提供了现有的开发框架供快速使用。
Feature Flag VS Feature Branches
Feature Flag(又名 Feature Toggle、Flip等)是一种允许控制线上功能开启或者关闭的方式，通常会采取配置文件的方式来控制。提到Feature Flag一般都会跟Feature Branches进行比较。这两个有什么关联与差别呢？可以通过一个简单的示例来比较：假设产品需要添加一个功能，如果你在主干上进行开发，那么通常的做法是在前端开发人员在界面上添加功能，然后可能会有其他同学来完成后端服务、安全保障，最后测试及Bug修复并发布上线。如下图所示：
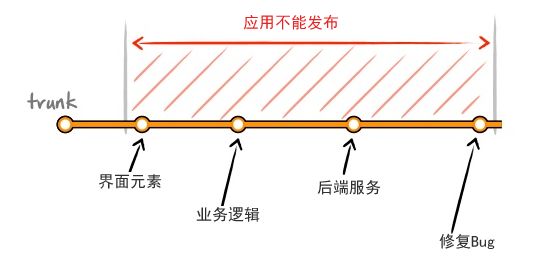
图中有个明显的问题是主干分支上在功能测试完毕之前是不能进行发布的，因为功能已经在提供在界面中，必须完备之后才能发布给用户使用。
当然解决方法也很简单，例如我们常见的是会使用功能分支(Feature Branches)来解决。在主干上拉取一个分支，然后在分支上开完测试完之后在合并到主干上，这样就不会影响主干的持续发布了。如果有另外的新的功能那么同样拉取新的分支来解决。如下图：
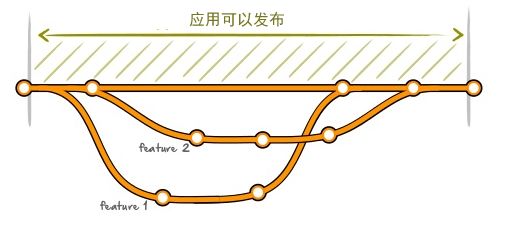
这样同样存在问题，如果一个功能比较复杂，开发的周期较长，而在此期间主干上已经多次修改代码，那么等分支上开发完之后合并到主干将是一个比较麻烦的工作。你必须去处理各种冲突，与其他开发人员沟通修改点。这是很多人不愿意做的。
于是有人提供了新的方案来解决这个问题。例如将开发工作拆分成多个小块，在各个分支上开发测试完成后及时合并到主干中，并且可以先隐藏界面功能，直到所有的功能开发完成之后才展现。这样每次合并的难度就小多了；或者每次将主干上的修改都及时同步到分支上，这样分支上开发完成之后合并到主干上就简单多了。
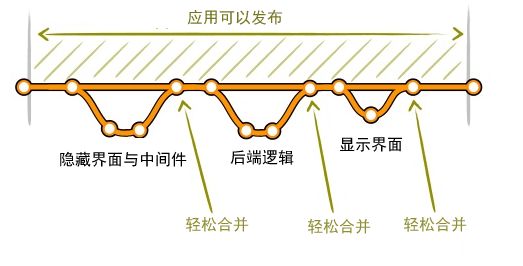
如果发布时出现bug怎么办？可能常见的是进行回滚重新上线。有什么方式既能避免分支合并的麻烦、保持主干快速迭代随时发布，又能更好的控制新功能的发布、方便的进行小流量或快速回滚操作呢？答案就是Feature Flag。
Feature Flag允许关闭未完成的功能，你可以在主干上进行迭代开发，新功能即便未开发完成也不会影响发布，因为它对用户是关闭的。当功能开发完成之后，修改配置便可以让功能发布。这种操作甚至可以在线上进行，例如代码已经发布但功能不可见，你可以修改配置让功能对特定的用户(线上测试、小流量或者全量发布等)可见。如果发现新功能存在问题，那么可以通过配置文件来迅速回滚，而必须重新分支上线。Feature Flag原理示意图如下：
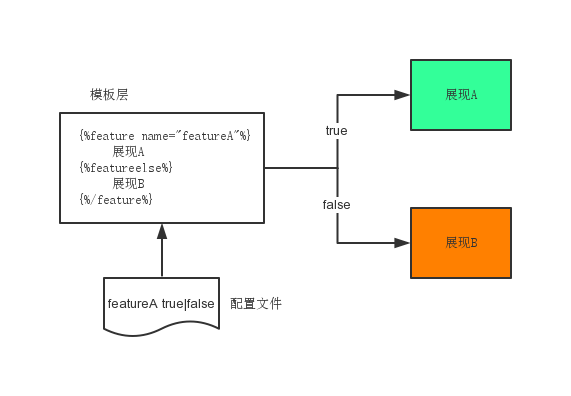
自的优缺点
选择合适的方案，而不拘泥于方式本身
并没有万能的方案，两种方式都有各自的优缺点。
Feature Branches
优点：
同时开发多个功能分支不会影响主干和线上代码
在分支上开发新功能时不用担心对其他在开发的功能的影响
现有很多持续集成系统支持分支的构建、测试、部署等
缺点也很明显，Martin Fowler的文章中已经做了全面的阐述：
分支分出去时间越长往往代码合并难度越大
在一个分支中修改了函数名字可能会引入大量编译错误。这点被称为语义冲突（semantic conflict）
为了减少语义冲突，会尽量少做重构。而重构是持续改进代码质量的手段。如果在开发的过程中持续不断的存在功能分支，就会阻碍代码质量的改进。
一旦代码库中存在了分支，也就不再是真正的持续集成了。当然你可以给每个分支建立一个对应的CI，但它只能测试当前分支的正确性。如果在一个分支中修改了函数功能，但是在另一个分支还是按照原来的假设在使用，在合并的时候会引入bug，需要大量的时间来修复这些bug。
Feature Toggle
优点：
避免了分支合并代码冲突的问题，因为是基于主干的开发
每次提交都在主干，迭代速度明显有优势
新功能的整个过程都持续集成
缺点:
未完成的功能可能会部署到线上，如果配置有误可能将未完成的功能开启。当然可以将界面层最后开发避免过早暴露。
主干上担心提交代码影响其他功能。
我们可以根据需要选择合适的方案。Feature Flag在避免分支合并加快迭代上有优势，另外Feature Flag除了主干开发上的支持，还有什么实用功能呢？下面来介绍。
Feature Flag种类与应用
一般Feature Flag可以分为两类，见下所示：
发布开关：
在发布代码时关掉未完成的功能
生存期短
功能稳定就马上删除
在整个开发过程中有预定义的值
业务开关：
实现A/B测试
针对特定人群发布功能尽早获得反馈
针对特定条件开启或者关闭功能。例如可以设置在指定时间点开启，这样新功能将按照设定自动上线下线，无需手动上线，适合专题等情况
能线上开启或者关闭,实现快速回滚
发布开关主要是为了隐藏未开发完成的功能，而业务开关则可以帮助我们快速满足某些需求。例如A/B测试，Feature Flag可以轻松控制展现哪个功能，提升A/B测试的可维护性。我们也可以通过配置里面的逻辑让新功能针对小部分人群甚至是特定地域的人群发布，尽早获取功能的反馈。甚至是可以在线上开启调试，只让新功能对调试人员可见。而这些都只需要配置文件和简单的标记来实现。
谁在用Feature Flag
功能看起来很酷，但是不是新东西？有谁在用呢，我可不不愿意承担风险
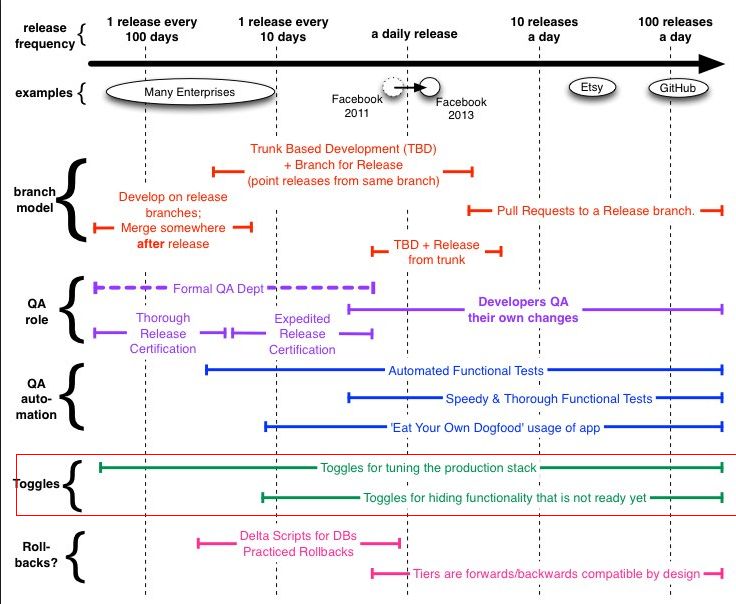
事实上Feature Flag已经在国外互联网公司中获得广泛的使用。例如FaceBook、Google等公司使用基于主干的开发模式来持续集成开发，Feature Flag是其中一个基础技术。下面这幅图展现了FaceBook开发模式转变历程,可以看到几年前facebook就开始使用Feature Toggle，使用了Feature Flag关闭主干上未开发完成的功能来保证快速迭代和高频率的发布。
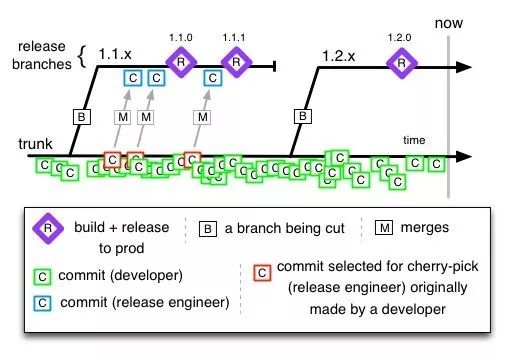
外主干开发中推荐这样一种方式：trunk作为开发主线，所有开发人员完成开发后向及时向主干提交代码，开发人员不允许在主干上拉取分支。在发布的时候由系统拉取分支发布，主干上的bug修复及时同步到发布分支。开发人员可以本地使用git等工具进行版本管理。如下图所示：
然基于主干的开发模式已经成为国外的主流，但分支开发并不是不该使用。使用分支不推荐的是让新功能代码在分支上长时间堆积，分支应当是生存周期短的。
实际应用中我们可以根据业务场景来选择是否用功能分支还是Feature Flag，并且这两者可以相互结合。例如在文章前面提到的示例中，可以使用分支来开发细分的子功能保持分支及时合并，同时使用Feature Flag来控制功能的发布，提升工作效率。
最佳实践
除了主干开发，什么情况下选择使用Feature Flag呢？下面是使用Feature Flag的一些典型场景：
在 UI 中隐藏或禁用新功能
在应用程序中隐藏或禁用新组件
对接口进行版本控制
扩展接口
支持组件的多个版本
将新功能添加到现有应用程序
增强现有应用程序中的现有功能
可以看到，由于Feature Flag本身是对业务功能的控制，所以不适于功能大范围的改动等情况。另外使用过程中需要注意一些问题：
只在需要的地方创建开关。美酒虽豪，不可贪杯。滥用任何技术都会出现问题。
控制开关的数量。同上，开关应按需使用并及时清除。
开关之间代码保持独立。如果代码存在依赖就没法删除，最终维护性反而变差
清除发布开关和废弃代码。发布开关应当在功能稳定后删除，旧代码也是。
界面层最后暴露。
如何实现
实现这套东西复杂吗？下面以php和smarty模板为例来介绍。
首先需要一套控制代码逻辑的工具，虽然开源的框架有在后端代码层的支持，但推荐在模板层使用Feature Flag，因为模板直接跟功能挂钩，维护起来更加直观方便。
例如我们会提供一个smarty插件，让你控制相应的展现:
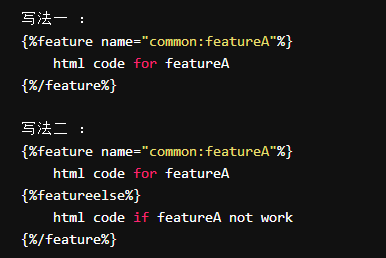
个代码的意思是如果common模块的featureA命中，则展现下面代码，否则展现另外一套代码，展现代码由于与功能相关，所以就相当于控制了展现哪个功能。当然你也可以不用featureelse只控制功能的开启或者关闭。
另外我们需要一个配置文件，对应featureA的配置，如下所示：
{
"features" : {
"featureA" : {
"type" : "switch",
"value" : "on",
"desc" : "test switch feature work or not"
}
}
}
featureA配置的value是on，开关类型是switch。也就是说这个功能是开启的。与switch类似的可以实现多个feature类型，例如抽样控制、日期控制、地域控制等，代码逻辑只需要根据value的设定判断是true还是false。例如抽样类型，value设置0.5，那么对应的类型逻辑只需要判断随机数是否在0-0.5范围内而已。
部署中我们只需要修改featureA的配置就可以控制功能的发布，是不是so easy!
开发框架
有哪些相应的开源框架呢？几乎各种语言都有相应的实现。例如FEX FIS小组提供了基于php和node.js的框架。此外还有多种语言的开源实现：
| 语言 | Feature Flag框架 |
|---|---|
| php | 基于smarty的Feature Flag框架 |
| NodeJs | 基于Node前后端解决方案Yogurt的Feature Flag框架 |
| java | Togglz |
| .NET | FeatureToggle |
| Ruby | Rollout、Degrade |
| Python | Gargoyle、Nexus admin |
| Groovy | GrailsFeatureToggle |
总结
Feature Flag与Feature Branches各有优势，结合使用能发挥更大作用
结合业务场景选择合适方案
Feature Flag能支持主干开发，并在控制功能发布上有独特优势
参考资料
采用功能切换进行软件开发
使用功能开关更好地实现持续部署
FeatureToggle
Feature driven development
Favor Feature Toggles over Feature Branches
What is Trunk Based Development?
Decoupling Deployment and Release- Feature Toggles
