前言
接着上篇的《.net core实践系列之SSO-同域实现》，这次来聊聊SSO跨域的实现方式。这次虽说是.net core实践，但是核心点使用jquery居多。
建议看这篇文章的朋友可以先看上篇《.net core实践系列之SSO-同域实现》做一个SSO大概了解。
源码地址：https://github.com/SkyChenSky/Core.SSO.git
效果图
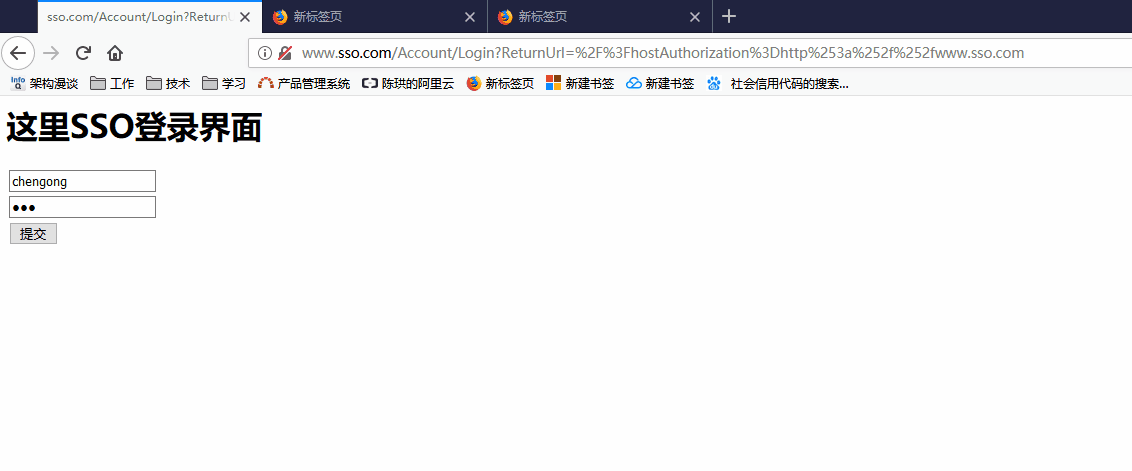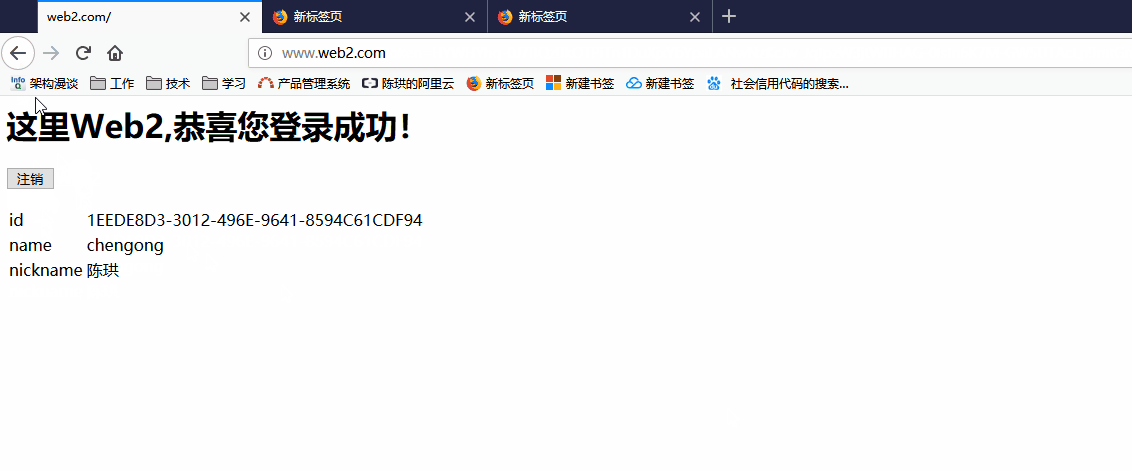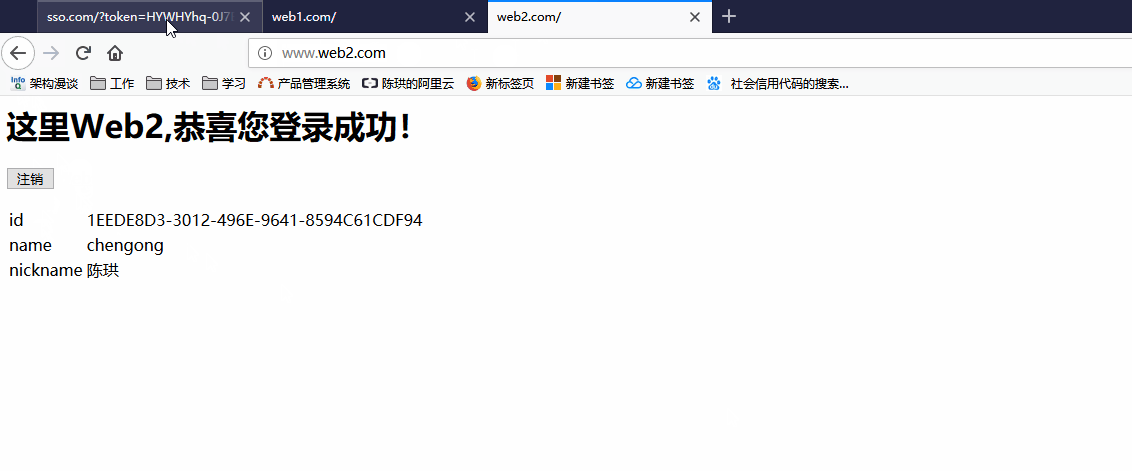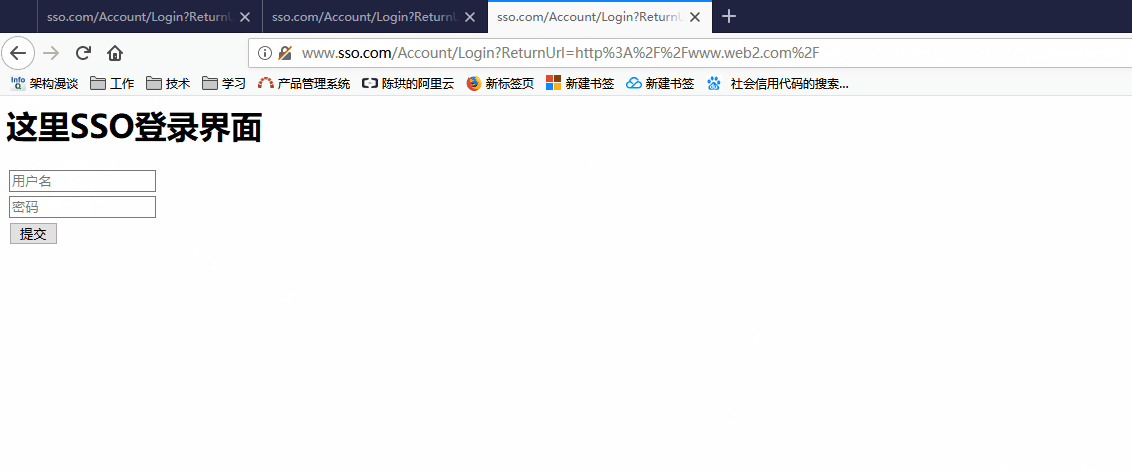
知识点回顾
实现原则
只要统一Token的产生和校验方式，无论授权与认证的在哪（认证系统或业务系统），也无论用户信息存储在哪（浏览器、服务器），其实都可以实现单点登录的效果
实现关键点
Token的生成
Token的共享
Token校验
Token共享复杂度
同域
跨域
Token认证方式
业务系统自认证
转发给认证中心认证
同源策略
所有支持JavaScript 的浏览器，都必须遵守的安全策略，也是浏览器最基本的安全功能。
如果没有处理过发起跨域请求，就算服务器接收到了，响应成功了浏览器也是会拦截的。
同源
指域名，协议，端口相同
目的
浏览器为了阻止恶意脚本获取不同源上的的敏感信息。
跨域请求
然而在实际情况下跨域请求的场景也是存在的，解决方案有两种：
JSONP
响应头设置“Access-Control-Allow-Origin”
Cookie
Cookie的读取和发送也是必须遵循同源策略的。
虽说请求共享可以设置响应头Access-Control-Allow-Credentials、Access-Control-Allow-Origin与Ajax请求属性xhrFields: {withCredentials: true}进行解决，但是！
就算响应头有set-cookie浏览器也是无法正常保存的。
SSO跨域解决方式
针对cookie认证，我唯一能找到的解决方案就是跳转页面。
具体步骤：
认证中心登录成功后，请求登录中心接口获得token
携带token逐个跳转到业务系统的中转页面。
跳转完成后，返回到认证中心登录页面进行引导。
PS：如果哪位朋友有更加好的方案，可以及时与我沟通，非常感谢
实现方式
登录中心授权
业务系统Token保存与注销
public class TokenController : Controller
{
public static TokenCookieOptions CookieOptions { get; set; }
public IActionResult Authorization(string token, List<string> hostAuthorization = null)
{
if (CookieOptions == null || string.IsNullOrEmpty(token))
return BadRequest();
HttpContext.Response.Cookies.Append(CookieOptions.Name, token, new CookieOptions
{
Domain = CookieOptions.Domain,
Expires = DateTimeOffset.UtcNow.Add(CookieOptions.Expires),
HttpOnly = CookieOptions.HttpOnly,
IsEssential = CookieOptions.IsEssential,
MaxAge = CookieOptions.MaxAge,
Path = CookieOptions.Path,
SameSite = CookieOptions.SameSite
});
if (hostAuthorization.Any())
hostAuthorization = hostAuthorization.Where(a => !a.Contains(HttpContext.Request.Host.Host)).ToList();
if (!hostAuthorization.Any())
hostAuthorization = new List<string> { "http://www.sso.com" };
return View(new TokenViewData
{
Token = token,
HostAuthorization = hostAuthorization
});
}
public IActionResult Logout(List<string> hostAuthorization = null)
{
HttpContext.Response.Cookies.Delete(CookieOptions.Name);
if (hostAuthorization.Any())
hostAuthorization = hostAuthorization.Where(a => !a.Contains(HttpContext.Request.Host.Host)).ToList();
if (!hostAuthorization.Any())
hostAuthorization = new List<string> { "http://www.sso.com" };
return View(new TokenViewData
{
HostAuthorization = hostAuthorization
});
}
}
Token生成与认证
与同域的实现的方式一致。
生成与认证是一对的，与之对应的就是AES的加密与解密。
业务系统自主认证的方式，对于系统的代码复用率与维护性都很低。如果想进行转发到认证系统进行认证，可以对[Authorize]进行重写。
大致思路是：
访问业务系统时，由自定义的[Authorize]进行拦截
获取到Token设置到请求头进行HttpPost到认证系统提供的/api/token/Authentication接口
响应给业务系统如果是成功则继续访问，如果是失败则401或者跳转到登录页。
结尾
最近事情比较多，demo与文章写的比较仓促，如果朋友们有更好的实现方式与建议，麻烦在下面评论反馈给我，先在此感谢。
原文地址: https://www.cnblogs.com/skychen1218/p/9805995.html
.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com
