两点之间距离
欧氏距离
即欧几里得距离。
平面内两点的距离为
立体空间内两点的距离为
\(\dots\)
\(n\) 维空间内两点的距离为
曼哈顿距离
二维空间内,两点之间距离为
\(n\) 维空间内两点的距离为
性质 \(-\) 三角形不等式:从点 \(i\) 到 \(i\) 的直接距离不会大于途经的任何其它点 \(k\) 的距离。
切比雪夫距离
二维空间内,两点之间距离为
曼哈顿距离与切比雪夫距离的相互转化
设 \(A(x_1,y_1),B(x_2,y_2)\) ,
-
曼哈顿坐标系是通过切比雪夫坐标系旋转 \(45^\circ\) 后,再缩小到原来的一半得到的
-
把每个点 \((x,y)\) 转化为 \((x+y,x-y)\) ,新坐标系下的切比雪夫距离 就是 原坐标系下的曼哈顿距离 。
-
把每个点 \((x,y)\) 转化为 \((\dfrac{x+y}{2},\dfrac{x-y}{2})\) ,新坐标系下的曼哈顿距离 就是 原坐标系下的切比雪夫距离 。
例题
P5098 [USACO04OPEN]Cave Cows 3
对于式子 \(|x_1-x_2|+|y_1-y_2|\) ,可以假设 \(x_1-x_2\ge 0\) ,根据 \(y_1-y_2\) 正负分类讨论:
- \(y_1-y_2\ge 0\) :
- \(y_1-y_2< 0\) :
分别求出 \(x+y\) 和 \(x-y\) 的最大、最小值之差即可。
P4648 [IOI2007] pairs 动物对数 (曼哈顿距离转切比雪夫距离)
P3964 [TJOI2013]松鼠聚会 (切比雪夫距离转曼哈顿距离)
向量叉积
对于点对 \((A,B,C)\) ,设:
\(x_1=A_x-B_x,y_1-A_y-B_y,x_2=C_x-B_x,y_2=C_y-B_y\)
若:
则:
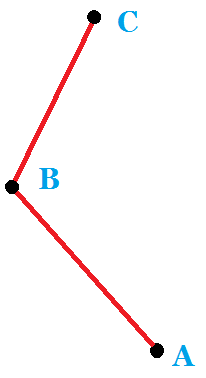
若:
则:
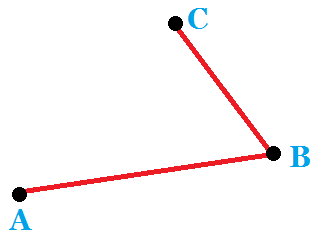
因此我们就可以利用叉积来维护凸包以及多边形面积。
点的旋转
让点 \((x_1,y_1)\) 绕点 \((x_2,y_2)\) 旋转 \(t^o\) :
\(x=(x_1-x_2)\times \cos{t}-(y_1-y_2)\times \sin{t}+x_2\)
\(y=(x_1-x_2)\times \sin{t}+(y_1-y_2)\times \cos{t}+y_2\)
![树链剖分概念及模板 + 例题 [POJ3237 tree + 软件包管理器]](http://pic.xiahunao.cn/树链剖分概念及模板 + 例题 [POJ3237 tree + 软件包管理器])
![P3706-[SDOI2017]硬币游戏【高斯消元,字符串hash】](http://pic.xiahunao.cn/P3706-[SDOI2017]硬币游戏【高斯消元,字符串hash】)
)


![P4548-[CTSC2006]歌唱王国【概率生成函数,KMP】](http://pic.xiahunao.cn/P4548-[CTSC2006]歌唱王国【概率生成函数,KMP】)
)
+ 勇者斗恶龙(dragon))

)
)



)

)
![DP专练1( [NOIP 2003]加分二叉树 + 太空梯 )](http://pic.xiahunao.cn/DP专练1( [NOIP 2003]加分二叉树 + 太空梯 ))
![P1896 [SCOI2005]互不侵犯](http://pic.xiahunao.cn/P1896 [SCOI2005]互不侵犯)
![AT2368-[AGC013B]Hamiltonish Path【构造】](http://pic.xiahunao.cn/AT2368-[AGC013B]Hamiltonish Path【构造】)