文章目录
- 概念
- 模板
- 例题1:软件包管理器
- 题目
- 题解
- 代码实现
- 例题2:POJ3237 tree
- 题目
- 题解
- 代码实现
概念
树链剖分主要是用于解决以下这两个问题。
1、更改树上点x到点y的最短路径上的所有结点的值
2、查询树上点x到点y的最短路径上的所有结点的和。
在讲树链剖分之前,我们先来看一下这样几个概念:
重儿子:父亲结点的所有儿子结点中,子树拥有结点数最多的结点。
轻儿子:父亲结点除了重儿子以外的所有儿子。
重边:父亲结点与重儿子的连边。
轻边:父亲结点与轻儿子的连边。
重链:所有重边所组成的一条链。

在这幅图中,圈内的数字为每个点的权值,粗边为重边,组成的链称为重链
任意一个点到根结点的路径,不会有超过logn条轻边;重链的个数不超过logn;
每个点一定都会只属于一个重链
接下来进入证明lognlognlogn条轻边环节(其余的相信大家都能自己finishitfinish\ itfinish it)
法一:(表达颇为复杂,可移至法二)
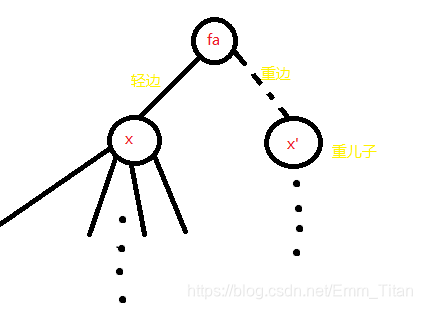
我们假设x−−fax--fax−−fa是轻边,x′−−fax'--fax′−−fa是重边,那么就有size[x]≤size[x′],size[x]<size[fa]size[x]\le size[x'],size[x]<size[fa]size[x]≤size[x′],size[x]<size[fa]
为什么没有取等,因为fafafa自己也算一个sizesizesize
所以最极限的情况就是size[fa]=size[x]+size[x′]+1,size[x]=size[x′]size[fa]=size[x]+size[x']+1,size[x]=size[x']size[fa]=size[x]+size[x′]+1,size[x]=size[x′],也是严格大于
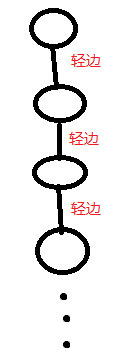
那么如果x−−fax--fax−−fa是轻边,那么size[fa]size[fa]size[fa]至少是size[x]size[x]size[x]两倍(粗略来看),如果fafafa也是轻边往上又×2×2×2以此类推
那么就是2i2^i2i(i只是我用来表示形式搞的),而点总共只有nnn,故i≤logni\le logni≤logn,所以上线就是lognlognlogn
法二:(本质与法一一样,但是表述要好懂一点吧。。。
根据轻儿子重儿子的定义,我们不难得到siz[轻儿子]<=siz[父亲]2siz[轻儿子]<=\frac{siz[父亲]}{2}siz[轻儿子]<=2siz[父亲],这么滚雪球般的/2/2/2,就是logloglog的级别
然后,知道重链和重链之间至少隔了一条轻边(否则两条重链应该合并成一条)
极限情况就是,每两条轻边之间就插一条重链,轻边的级别都被限制在了logloglog
所以重链的级别也不会超过logloglog
模板
接下来我们讲讲实现:
在进行树链剖分时,我们将进行这些变量声明:
f[u]:保存点u的父亲结点
d[u]:保存点u的深度
size[u]:保存以u为根节点的子树的结点个数
son[u]:保存点u的重儿子
top[u]:保存点u所在重链的顶端结点
id[u]:保存点u在线段树上对应的编号
rk[u]:表示线段树上点u在原树上对应的编号(与id进行映射)
接下来,就是要求出所有结点它的子树的大小,并找出重儿子(即处理出size[u]和son[u])。我们在这里可以直接通过DFS,对树进行深度搜索,得到我们想要的两个答案。
void dfs1 ( int u, int fa, int depth ) { //当前节点,父节点,层次深度 f[u] = fa;d[u] = depth;size[u] = 1;//这个点本身size=1 for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( v == fa ) continue;dfs1 ( v, u, depth + 1 );//层次深度+1 size[u] += size[v];//回溯的子节点size已被处理,用它来更新父节点size if ( size[v] > size[son[u]] || ! son[u] )son[u] = v;//选取size最大的作为重儿子 }
}
接下来,我们再进行一遍DFS,找到所有结点重链的顶端,并对结点进行重新排序。
void dfs2 ( int u, int t ) { //当前节点,重链顶端 top[u] = t;id[u] = ++ cnt; //标记dfs序 rk[cnt] = u;//序号cnt对应节点u 一般来说是没有用的。。 if ( ! son[u] ) return;dfs2 ( son[u], t );/*我们选择优先进入重儿子来保证一条重链上各个节点dfs序号连续一个点和它的重儿子处于同一条重链所以重儿子所在重链的顶端还是t */for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( v != son[u] && v != f[u] )dfs2 ( v, v );//一个点位于轻链顶端,那么他的top必定是它本身 }
}
两遍DFS之后,我们就可以知道我们前面列出的所有变量的值
且对于每一条重链,他们当中的点都是连续的区间
对于点uuu而言,uuu的子树的dfsdfsdfs序都是连续的一段区间
那么,对于每一条重链,我们可以通过线段树去维护这一条链内的所有信息
对于两个点不在一条链上的,我们可以通过对深度较深的那个点进行操作
将这个点跳转到他的top位置的父亲结点上,直到两个点在一条重链上为止
写法很多,分享其一
int sum ( int x, int y ) {int ans = 0, fx = top[x], fy = top[y];while ( fx != fy ) {if ( d[fx] >= d[fy] ) {ans += query ( 1, cnt, id[fx], id[x], 1 );//线段树的区间从0或者1开始由题决定//线段树l,r,我们要查找的区间L,R,线段树编号numx = f[fx];fx = top[x]; }else {ans += query ( 1, cnt, id[fy], id[y], 1 );y = f[fy];fy = top[y];}}//循环结束,两点已经位于同一条重链上,但两点不一定为同一个点//所以我们还要统计这两点间的贡献 if ( id[x] <= id[y] )ans += query ( 1, cnt, id[x], id[y], 1 );else ans += query ( 1, cnt, id[y], id[x], 1 );return ans;
}
线段树的模板我就不给了,注意要打lazy标记哦!!!
接下来就去战场上试试手吧。。

例题1:软件包管理器
题目
题目描述
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,⋯,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
输入格式
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n−1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
输入输出样例
输入
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0
输出
3
1
3
2
3
输入
10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9
输出
1
3
2
1
3
1
1
1
0
1
说明/提示
【样例说明 1】
一开始所有的软件包都处于未安装状态。
安装5号软件包,需要安装0,1,5三个软件包。
之后安装6号软件包,只需要安装6号软件包。此时安装了0,1,5,6四个软件包。
卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。
之后安装4号软件包,需要安装1,4两个软件包。此时0,1,4处在安装状态。最后,卸载0号软件包会卸载所有的软件包。`
【数据范围】
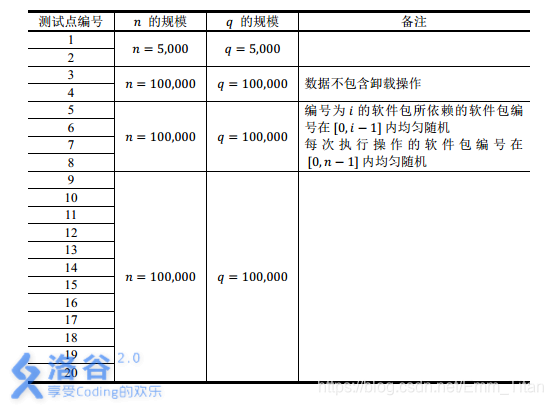
题解
这就是一个树链剖分模板题:
但是怎么感觉跟模板有一丢丢不太一样的感jio呢

每个iii有且只有一个依附,也就是只会有一个爸爸,加上题目保证不会有环,那么这肯定是一棵树了!
安装时要从iii往上找每一个的依赖安装包,直到根节点000为止,可以用模板往上找。
卸载时要从iii往下开始把每一个依赖i的安装包或者间接依赖I的安装包都删掉,直到叶子结点
即,删掉iii(包含iii)的子树
这中间的计算再用线段树维护,更改即可,还可以优美的打个lazylazylazy懒标记
代码实现
#include <cstdio>
#include <vector>
using namespace std;
#define MAXN 100005
int tree[MAXN << 2];
int sum[MAXN << 2];
vector < int > G[MAXN];
int n, q, x, cnt;
char s[10];
int f[MAXN], id[MAXN], dep[MAXN], tot[MAXN], son[MAXN], top[MAXN];void dfs1 ( int u, int fa, int depth ) {dep[u] = depth;tot[u] = 1;for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( v == fa ) continue;dfs1 ( v, u, depth + 1 );tot[u] += tot[v];if ( tot[v] > tot[son[u]] || ! son[u] )son[u] = v;}
}void dfs2 ( int u, int t ) {id[u] = ++ cnt;top[u] = t;if ( ! son[u] ) return;dfs2 ( son[u], t );for ( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i];if ( v == son[u] || v == f[u] ) continue;dfs2 ( v, v );}
}void pushdown ( int l, int r, int num ) {if ( sum[num] == 0 )sum[num << 1] = sum[num << 1 | 1] = 0;if ( sum[num] == r - l + 1 ) {int mid = ( l + r ) >> 1;sum[num << 1] = mid - l + 1;sum[num << 1 | 1] = r - mid;}
}void update ( int l, int r, int L, int R, int num, bool opt ) {if ( L <= l && r <= R ) {sum[num] = ( r - l + 1 ) * opt;return;}int mid = ( l + r ) >> 1;if ( L <= mid ) update ( l, mid, L, R, num << 1, opt );if ( mid < R ) update ( mid + 1, r, L, R, num << 1 | 1, opt );sum[num] = sum[num << 1] + sum[num << 1 | 1];
}int query ( int l, int r, int L, int R, int num ) {if ( L <= l && r <= R ) return sum[num];pushdown ( l, r, num );int mid = ( l + r ) >> 1;int sum1 = 0, sum2 = 0;if ( L <= mid ) sum1 = query ( l, mid, L, R, num << 1 );if ( mid < R ) sum2 = query ( mid + 1, r, L, R, num << 1 | 1 );return sum1 + sum2;
}void solve_sum ( int x ) {int ans = 0, fx = top[x];while ( fx ) {ans += id[x] - id[fx] - query ( 0, cnt, id[fx], id[x], 1 ) + 1;update ( 0, cnt, id[fx], id[x], 1, 1 );x = f[fx];fx = top[x];}ans += id[x] - id[0] - query ( 0, cnt, id[fx], id[x], 1 ) + 1;update ( 0, cnt, id[0], id[x], 1, 1 );printf ( "%d\n", ans );
}int main() {scanf ( "%d", &n );for ( int i = 1;i < n;i ++ ) {scanf ( "%d", &f[i] );G[f[i]].push_back ( i );}dfs1 ( 0, -1, 1 );dfs2 ( 0, 0 );scanf ( "%d", &q ); for ( int i = 1;i <= q;i ++ ) {scanf ( "\n%s %d", s, &x );if ( s[0] == 'i' )solve_sum ( x );else {printf ( "%d\n", query ( 0, cnt, id[x], id[x] + tot[x] - 1, 1 ) );update ( 0, cnt, id[x], id[x] + tot[x] - 1, 1, 0 ); }}return 0;
}
不如趁热打铁:
再来一道例题吧~(づ ̄3 ̄)づ╭❤~

例题2:POJ3237 tree
题目
给你由N个结点组成的树。树的节点被编号为1到N,边被编号为1到N-1。每一条边有一个权值。然后你要在树上执行一系列指令。指令可以是如下三种之一:
CHANGE i v:将第i条边的权值改成v。
NEGATE a b:将点a到点b路径上所有边的权值变成其相反数。
QUERY a b:找出点a到点b路径上各边的最大权值。
输入格式
输入文件的第一行有一个整数N(N<=10000)。
接下来N-1行每行有三个整数a,b,c,代表点a和点b之间有一条权值为c的边。这些边按照其编号从小到大给出。
接下来是若干条指令(不超过10^5条),都按照上面所说的格式。
输入文件的最后一行是"DONE".
输出格式
对每个“QUERY”指令,输出一行,即路径上各边的最大权值。
样例
input1
3
1 2 1
2 3 2
QUERY 1 2
CHANGE 1 3
QUERY 1 2
DONE
output1
1
3
input2
5
2 1 8
1 3 4
4 1 3
5 3 7
NEGATE 1 4
CHANGE 1 9
NEGATE 2 1
CHANGE 1 9
NEGATE 5 1
NEGATE 2 1
QUERY 5 1
QUERY 3 1
CHANGE 3 6
NEGATE 3 1
DONE
output2
-4
-4
数据范围与提示
N <= 10000
题解
首先这道题可以发现以任何一个点作为根节点都不会影响这棵树的长相
我们就老规矩以1作为根节点建树
其次这道题不同于模板的就是这是一个边权的树链剖分
那我们就要把边权变为我们的模板
因为这道题我完全是自己做的,

所以我的思路是把边权塞成点权
具体操作如下:
因为这是一棵树那么每一个点的爸爸都只有111个,
所以我就考虑把这条边的边权塞给儿子vvv节点的点权,
这样接下来的操作完全就是线段树模板+树链模板
然后这道题有取相反数的操作,也就意味着原本的最小值有可能咸鱼翻身变成最大值
这就提醒我们线段树要开成结构体,存下maxmaxmax和minminmin
但是这道题既然把边权塞成了点权,就要考虑一些情况:

1):我们线段树的范围是[1,cnt][1,cnt][1,cnt],包含了根节点111,
而我们把边塞成了点,自然根节点111是不应该被算的,
所以我们可以把根节点111的线段树区间的最小值置为极大值INF,最大值置为极小值-INF
这样在比对最大值和最小值往上传给父亲区间的时候,我们就能保证不选根节点111的区间
2):当我们找答案x,yx,yx,y,爬到了同一个重链的时候,要注意:
我们以id[x]<=id[y]id[x]<=id[y]id[x]<=id[y]为例,当他们爬到同一个重链的时候,id[x]id[x]id[x]的值代表了xxx和xxx爸爸这条边的值
很明显我们只需要xyx~yx y包含的边值,就要把这条边给排除掉
这时只需要id[x]+1id[x]+1id[x]+1就可以避免了

还不理解我们就用图来表示:
我们现在求的是x−yx-yx−y的边中最大值,也就是jjj和kkk两条边的最大值
上面提过把边权塞给儿子节点,
那么xxx的点权id[x]id[x]id[x]也就是fxxfx~xfx x这条边的边权,即iii
我们如果按照模板的打法L,RL,RL,R传的就是id[x],id[y]id[x], id[y]id[x],id[y],这样我们就多算了一条iii
所以我们才要进行id[x+1]id[x+1]id[x+1],把这条边排除掉
会不会存在id[x]+1>id[y]id[x]+1>id[y]id[x]+1>id[y]的情况呢?

最简单的就是xxx是yyy的直系爸爸
那么id[x]+1id[x]+1id[x]+1就刚好是id[y]id[y]id[y],id[y]id[y]id[y]的点权存的又是xyx~yx y两点之间的边权,刚好就是我们想要的
然后这道题就这么结束了。。。

代码实现
添加链接描述
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
#define inf 0x7f7f7f7f
#define maxn 10005
#define lson now << 1
#define rson now << 1 | 1
pair < int, int > edge[maxn];
struct node { int to, w; };
vector < node > G[maxn];
int T, n, cnt;
int dep[maxn], f[maxn], siz[maxn], val[maxn], son[maxn];
int id[maxn], dfn[maxn], top[maxn];
int Max[maxn << 2], Min[maxn << 2];
bool tag[maxn << 2];void dfs1( int u, int fa ) {dep[u] = dep[fa] + 1, f[u] = fa, siz[u] = 1;for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i].to, w = G[u][i].w;if( v == fa ) continue;else dfs1( v, u );val[v] = w;siz[u] += siz[v];if( ! son[u] or siz[v] > siz[son[u]] ) son[u] = v;}
}void dfs2( int u, int t ) {top[u] = t, dfn[u] = ++ cnt, id[cnt] = u;if( ! son[u] ) return;else dfs2( son[u], t );for( int i = 0;i < G[u].size();i ++ ) {int v = G[u][i].to;if( v == f[u] or v == son[u] ) continue;else dfs2( v, v );}
}void build( int now, int l, int r ) {tag[now] = 0;if( l == r ) { if( l ^ 1 ) Max[now] = Min[now] = val[id[l]];else Max[now] = -inf, Min[now] = inf;return;}int mid = ( l + r ) >> 1;build( lson, l, mid );build( rson, mid + 1, r );Max[now] = max( Max[lson], Max[rson] );Min[now] = min( Min[lson], Min[rson] );
}void modify( int now ) {Max[now] = -Max[now];Min[now] = -Min[now];swap( Max[now], Min[now] );tag[now] ^= 1;
}void pushdown( int now ) {if( ! tag[now] ) return;modify( lson );modify( rson );tag[now] = 0;
}void modify( int now, int l, int r, int pos, int v ) {if( l == r ) { Max[now] = Min[now] = v; return; }pushdown( now );int mid = ( l + r ) >> 1;if( pos <= mid ) modify( lson, l, mid, pos, v );else modify( rson, mid + 1, r, pos, v );Max[now] = max( Max[lson], Max[rson] );Min[now] = min( Min[lson], Min[rson] );
}void reverse( int now, int l, int r, int L, int R ) {if( R < l or r < L or L > R ) return;if( L <= l and r <= R ) { modify( now ); return; }pushdown( now );int mid = ( l + r ) >> 1;reverse( lson, l, mid, L, R );reverse( rson, mid + 1, r, L, R );Max[now] = max( Max[lson], Max[rson] );Min[now] = min( Min[lson], Min[rson] );
}void reverse( int x, int y ) {while( top[x] ^ top[y] ) {if( dep[x] < dep[y] ) swap( x, y );reverse( 1, 1, n, dfn[top[x]], dfn[x] );x = f[top[x]];}if( dep[x] > dep[y] ) swap( x, y );reverse( 1, 1, n, dfn[x] + 1, dfn[y] );
}int query( int now, int l, int r, int L, int R ) {if( r < L or R < l or L > R ) return -inf;if( L <= l and r <= R ) return Max[now];pushdown( now );int mid = ( l + r ) >> 1;return max( query( lson, l, mid, L, R ), query( rson, mid + 1, r, L, R ) );
}void query( int x, int y ) {int ans = -inf;while( top[x] ^ top[y] ) {if( dep[top[x]] < dep[top[y]] ) swap( x, y );ans = max( ans, query( 1, 1, n, dfn[top[x]], dfn[x] ) );x = f[top[x]];}if( dep[x] > dep[y] ) swap( x, y );ans = max( ans, query( 1, 1, n, dfn[x] + 1, dfn[y] ) );printf( "%d\n", ans );
}int main() {scanf( "%d", &T );while( T -- ) {scanf( "%d", &n );cnt = 0;for( int i = 1;i <= n;i ++ ) G[i].clear(), son[i] = 0;for( int i = 1, u, v, w;i < n;i ++ ) {scanf( "%d %d %d", &u, &v, &w );edge[i] = make_pair( u, v );G[u].push_back( { v, w } );G[v].push_back( { u, w } );}dfs1( 1, 0 );dfs2( 1, 1 );build( 1, 1, n );char opt[10]; int a, b;while( 1 ) {scanf( "%s", opt );if( opt[0] == 'D' ) break;else {scanf( "%d %d", &a, &b );switch( opt[0] ) {case 'C' : {if( dep[edge[a].first] < dep[edge[a].second] )modify( 1, 1, n, dfn[edge[a].second], b );elsemodify( 1, 1, n, dfn[edge[a].first], b );break;}case 'N' : reverse( a, b ); break;case 'Q' : query( a, b ); break;}}}}return 0;
}
好了,树链剖分就到这里了

![P3706-[SDOI2017]硬币游戏【高斯消元,字符串hash】](http://pic.xiahunao.cn/P3706-[SDOI2017]硬币游戏【高斯消元,字符串hash】)
)


![P4548-[CTSC2006]歌唱王国【概率生成函数,KMP】](http://pic.xiahunao.cn/P4548-[CTSC2006]歌唱王国【概率生成函数,KMP】)
)
+ 勇者斗恶龙(dragon))

)
)



)

)
![DP专练1( [NOIP 2003]加分二叉树 + 太空梯 )](http://pic.xiahunao.cn/DP专练1( [NOIP 2003]加分二叉树 + 太空梯 ))
![P1896 [SCOI2005]互不侵犯](http://pic.xiahunao.cn/P1896 [SCOI2005]互不侵犯)
![AT2368-[AGC013B]Hamiltonish Path【构造】](http://pic.xiahunao.cn/AT2368-[AGC013B]Hamiltonish Path【构造】)
)