建议在看这篇博客之间要了解一下带旋Treap
我会在模板前面写上一部分的思路讲解，帮助各位理解

概念

根据它的名字我们也可以得知，这种数据结构就是$treap$的后代，只不过不带旋转，其余都是一致的
所以在运用和代码上会有所异同。它比$treap$多了$split$（拆树）和$merge$（合并）操作，所以得到的结果是可以多处理数据结构的区间问题。以一换一
接下来我们就重点介绍$split$和$merge$还有区间操作到底是个什么玩意儿？？？

全套模板

因为是自己修改后的模板，可能会有不严谨处，欢迎大家指出并更正！

先照样介绍各个数组变量的含义：
$Size$：表示节点数量也可作最后一个点编号
$cnt[p]$：表示编号为$p$，值为$x$在$treap$中插入的次数
$key[p]$：表示该点$p$的值为$x$
$rd[p]$：就是我们自己搞的修正值，用$rand()$函数随机生成
$siz[p]$：编号为$p$的子树包括本身在内的节点数量即大小
$son[p][2]$：$son[p][0]$表示p的左儿子，$son[p][1]$表示$p$的右儿子

---

push_up模板

先蓄蓄力，放松放松

void push_up ( int x ) {siz[x] = siz[son[x][0]] + siz[son[x][1]] + cnt[x];
}

---

split拆树模板(按权值拆)

$split$拆树的结果就是把树根据要求值$k$拆成两半

左边全是值$\le k$的点，右边全是值$>k$的点

上图讲解：充分运用画过的图，我带领大家走一遍，再不懂就不管本蒟蒻了

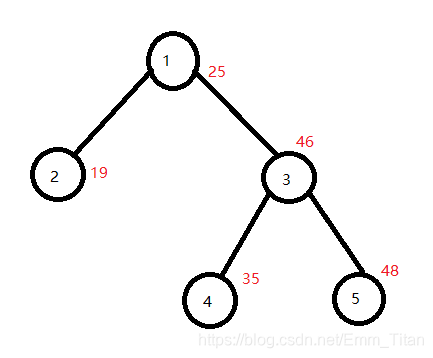
假设我们的$k$为35，那么首先从根节点1开始，发现1的权值25小于35

这个时候我们就能确定根节点以及根节点的左子树的权值全都是小于35的

那么这个时候它们是属于拆分后左边的子树的

但是我们会发现根节点的右子树也存在可能值大于35的节点

我们就需要继续往下拆分

接下来走到节点3，发现权值大于35，可以得出的结论是3节点以及它的右子树的权值都是大于35的，应该是属于拆分后的右子树，

但是同样的我们不能肯定它的左儿子是否也是归属于右边，继续往左拆分

最后走到了叶子节点，发现节点4的权值小于等于35也应该归于左边

这个时候就把节点4接到根节点1的右边，成功把1和3的边给断掉

最后一层一层回溯，最顶层的两个根节点就分别为1，3

节点1统领了所有权值小于等于$k$的子树，节点3统领了所有权值大于$k$的子树

我的写法是传地址，这样就直接更改了

---

void split ( int p, int &l, int &r, int x ) {if ( ! p ) {l = r = 0;return;}if ( key[p] <= x ) {l = p;split ( son[p][1], son[p][1], r, x );push_up ( l );}else {r = p;split ( son[p][0], l, son[p][0], x );push_up ( r );}
}

---

split拆树模板(按个数拆)

此代码有适用范围！！！在某些题中会出错

按下标拆的思路与按权值拆是一样的，只不过往右子树找的时候记得把左子树和根占得位置给减掉即可

拆出来的左子树的个数恰好是给定的$k$，右子树就是剩下来的所有点

void split_id ( int p, int &l, int &r, int x ) {if ( ! p ) {l = r = 0;return;}if ( siz[son[p][0]] + 1 <= x ) {l = p;split_id ( son[p][1], son[p][1], r, x - siz[son[p][0]] - 1 );push_up ( l );}else {r = p;split_id ( son[p][0], l, son[p][0], x );push_up ( r );}
}

---

merge合并模板（地址版）

我们可以发现拆分子树的时候，改变了树的形态，这也是无法进行$treap$的旋转操作的一个原因，
百因必有果，你的报应就是我

既然方便了$split$拆分，改变了树的形态，我们就必须再写一个补丁函数，把树进行还原修复

但是我们不再是使用权值$k$进行，我们思考$treap$用旋转的目的是为了维护树的键值不是从大到小就是从小到大

反正就是要有一定的顺序

那么$merge$的目的也是维护树的键值有顺序

本来$split$拆的树也是我们维护好了顺序的

所以$merge$合并的时候根据键值顺序来合并，也能还原$split$所拆的树

在这里我仍然选择的传地址直接改在原来的地方，如果把上边的$split$理解了，那么我相信这个也就很好理解了

void merge ( int &p, int x, int y ) {if ( ! x || ! y ) {p = x + y;return;}if ( rd[x] < rd[y] ) {p = x;merge ( son[p][1], son[p][1], y );}else {p = y;merge ( son[p][0], x, son[p][0] );}push_up ( p );
}

---

merge合并模板（带返回根）

int merge ( int x, int y ) {if ( ! x || ! y )return x + y;if ( rd[x] < rd[y] ) {son[x][1] = merge ( son[x][1], y );push_up ( x );return x;}else {son[y][0] = merge ( x, son[y][0] );push_up ( y );return y;}
}

---

区间模板

其实就是先把这个区间$[l,r]$拆出来然后搞一波，再把它合并回去

可以理解为先把部队里某一个方阵的士兵扯出来再捅几刀最后再让他们归队，好残忍

void XXX ( int x, int y ) {int l, r, L, R;spilt ( root, l, r, y );split ( l, L, R, x - 1 );//区间里面进行的操作merge ( l, L, R );merge ( root, l, r ); 
}

我们以翻转$reverse$为例，小声bb：是为了让你们做文艺平衡树更简单

void reverse ( int x, int y ) {int l, r, L, R;spilt ( root, l, r, y );split ( l, L, R, x - 1 );lazy[R] = !lazy[R];//对[x,y]区间进行打标，1表示翻转，0表示没有翻转 merge ( l, L, R );merge ( root, l, r ); 
}

---

简单过渡一下：其实多做几道题多用用模板会对代码更加理解，为了方便各位理解下面更改的函数，在这里简单总结一下$split$和$merge$的思路

$split(root,l,r,x)$表示把以$root$为根的子树按照权值$x$拆分，$l$存储着小于等于$x$的子树的根，$r$存储着大于$x$的子树的根

$merge(root,l,r)$表示把一棵子树的根为$l$和另一棵子树的根为$r$合并为一棵根为$root$的新根

那么其余的操作都可以用$split$和$merge$改变我们以前的写法，新朋友就要多用用嘛！

---

insert插入模板

$insert$之前我们是用的递归方式，在这里就要充分运用$split$和$merge$

我声明一下，很多很多篇博客都是直接新建一个节点，本蒟蒻就不理解了，对于一个点它可能已经出现在树上了，这个时候就直接$cnt++$，为什么要选择新建点呢？

所以我就费了九牛二虎之力写出了自己想要的模板

当然对于某部分的题各个点之间是互不相同的，或其它特殊的要求，我的代码就与大佬们成为一流的了，这个时候就可以删掉我代码中if的判断即可，不删也不影响，最多代码长了一丢丢而已啦~

• 首先我们把树先拆成权值都$\le x$的子树和权值都$>x$的子树
• 再把权值$\le x$的子树拆分成权值$\le x-1$的树和权值$>x-1$也就是权值等于$x$的树
• 接着我们就判断储存权值等于$x$的树的节点是否为空，
  • 如果为空就意味着树上并没有该点，就新建一个点；
  • 否则就直接$cnt++$再$update$一下
• 拆了就要合并，我们怎么拆的就怎么倒着并回去，很简单的，本蒟蒻都能自己打出来

void insert ( int x ) {int l, r, L, R;split ( root, l, r, x );split ( l, L, R, x - 1 );if ( R ) {cnt[R] ++;push_up ( R );merge ( l, L, R );merge ( root, l, r );}else {++ Size;cnt[Size] = siz[Size] = 1;rd[Size] = rand ();key[Size] = x;merge ( l, L, Size );merge ( root, l, r );}
}

---

delete删除模板

仿照$insert$的思路

• 先把值为$x$的这个点拆出来
• 接下来判断如果这个点插入的次数是否大于1
  • 如果大于可以直接$cnt--$，该点不会消失，倒着合并回去；
  • 否则该点就应该消失在树上，我们可以通过不让它参与合并，排挤它 ，那么它就不会出现在树上了，直接把值小于等于$x-1$的树和值大于$x$的树合并即可
    

void delet ( int x ) {int l, r, L, R;split ( root, l, r, x );split ( l, L, R, x - 1 );if ( R && cnt[R] > 1 ) {cnt[R] --;push_up ( R );merge ( l, L, R );merge ( root, l, r );}elsemerge ( root, L, r );
}

---

剩下的查找其实是可以照搬的，但是我还是给大家分享一些其它的写法吧！！

---

find_kth找第k大模板

这个我还是很喜欢这种写法的，所以就不更改了

int find_kth ( int rt, int x ) {if ( siz[son[rt][0]] >= x )return find_kth ( son[rt][0], x );else if ( siz[son[rt][0]] + cnt[rt] < x )return find_kth ( son[rt][1], x - siz[son[rt][0]] - cnt[rt] );elsereturn key[rt];
}
//非递归结构体版本 ↓
void find_val( int x ) {int now = rt;while( 1 ) {if( x <= t[t[now].lson].siz ) now = t[now].lson;else if( x <= t[t[now].lson].siz + t[now].cnt ) break;else x -= ( t[t[now].lson].siz + t[now].cnt ), now = t[now].rson;}printf( "%d\n", t[now].val );
}

Upd：
下面求排名为 $x$ 的数的方法不一定是对的。
因为按照个数大小分裂代码的正确性当且仅当数据中每个数互不相等。
显然，设想某个数有若干个，占据了排名为一段的区间，如果按照 $x/x-1$ 的个数分，全都划在该数身上，则 $R$ 就是个空子树了。
如果直接判 $R$ 是否为空也是错误的。
但是我也不知道为什么？？！！所以还是麻烦大家写上面的方法。
也有可能是因为博主的其它模板某些限制把。。。
数据结构真是一个比一个玄学！！凸(艹皿艹 )

void find_val( int x ) {int l, r, L, R;split_siz( rt, x, l, r );split_siz( l, x - 1, L, R );printf( "%d\n", t[R].val );rt = merge( merge( L, R ), r );
}

---

get_rank找排名模板

我们就充分运用新学函数，思考一下如果把$\le x-1$的树拆出来
那么它的大小$+1$是不是就是$x$的$rank$排名呢！！！实在是

void get_rank ( int x ) {int l, r;split ( root, l, r, x - 1 );printf ( "%d\n", siz[l] + 1 );merge ( root, l, r );
}

---

pre找前驱模板

找前驱，这里是严格小于的情况，先拆分一下看有木有权值小于$x$的点
有的话我们就调用$find$_$kth$在拆分出来的那棵子树中去找最后一个也就是$x$的前一个

int pre ( int x ) {int l, r, result;split ( root, l, r, x - 1 );if ( siz[l] )result = find_kth ( l, siz[l] );elseresult = INF;merge ( root, l, r );return result;
}

---

suf找后驱模板

找后驱，与找前驱相似，这里是严格大于的情况，先拆分一下看有木有权值大于$x$的点
有的话我们就调用$find$_$kth$在拆分出来的那棵子树中去找第一个也就是$x$的后一个

int suf ( int x ) {int l, r, result;split ( root, l, r, x );if ( siz[r] )result = find_kth ( r, 1 );elseresult = INF;merge ( root, l, r );return result;
}

Upd：当然你可以直接暴力的裂开。以找前驱为例，把 $\le x-1$ 的子树列出来，从子树的根开始疯狂走右儿子（如果有）。

void find_pre( int x ) {int l, r;split_val( rt, x - 1, l, r );int now = l;while( t[now].rson ) now = t[now].rson;printf( "%d\n", t[now].val );rt = merge( l, r );
}void find_suf( int x ) {int l, r;split_val( rt, x, l, r );int now = r;while( t[now].lson ) now = t[now].lson;printf( "%d\n", t[now].val );rt = merge( l, r );
}

---

老套路来些题目练习练习，实在是太模板了，直接器官移植都能过，哎╮(╯▽╰)╭

例题1：普通平衡树

题目

点击查看

代码实现

一样一样的，进行器官移植即可

#include <cstdio>
#include <algorithm>
using namespace std;
#define MAXN 100005
#define INF 0x7f7f7f7f
int root, n, Size;
int son[MAXN][2], cnt[MAXN], siz[MAXN], rd[MAXN], key[MAXN];void push_up ( int x ) {siz[x] = siz[son[x][0]] + siz[son[x][1]] + cnt[x];
}void split ( int p, int &l, int &r, int x ) {if ( ! p ) {l = r = 0;return;}if ( key[p] <= x ) {l = p;split ( son[p][1], son[p][1], r, x );push_up ( l );}else {r = p;split ( son[p][0], l, son[p][0], x );push_up ( r );}
}void merge ( int &p, int x, int y ) {if ( ! x || ! y ) {p = x + y;return;}if ( rd[x] < rd[y] ) {p = x;merge ( son[p][1], son[p][1], y );}else {p = y;merge ( son[p][0], x, son[p][0] );}push_up ( p );
}void insert ( int x ) {int l, r, L, R;split ( root, l, r, x );split ( l, L, R, x - 1 );if ( R ) {cnt[R] ++;push_up ( R );merge ( l, L, R );merge ( root, l, r );}else {++ Size;cnt[Size] = siz[Size] = 1;rd[Size] = rand ();key[Size] = x;merge ( l, L, Size );merge ( root, l, r );}
}void delet ( int x ) {int l, r, L, R;split ( root, l, r, x );split ( l, L, R, x - 1 );if ( R && cnt[R] > 1 ) {cnt[R] --;push_up ( R );merge ( l, L, R );merge ( root, l, r );}elsemerge ( root, L, r );
}int find_kth ( int rt, int x ) {if ( siz[son[rt][0]] >= x )return find_kth ( son[rt][0], x );else if ( siz[son[rt][0]] + cnt[rt] < x )return find_kth ( son[rt][1], x - siz[son[rt][0]] - cnt[rt] );elsereturn key[rt];
}int pre ( int x ) {int l, r, result;split ( root, l, r, x - 1 );if ( siz[l] )result = find_kth ( l, siz[l] );elseresult = INF;merge ( root, l, r );return result;
}int suf ( int x ) {int l, r, result;split ( root, l, r, x );if ( siz[r] )result = find_kth ( r, 1 );elseresult = INF;merge ( root, l, r );return result;
}void get_rank ( int x ) {int l, r;split ( root, l, r, x - 1 );printf ( "%d\n", siz[l] + 1 );merge ( root, l, r );
}int main() {scanf ( "%d", &n );while ( n -- ) {int opt, x;scanf ( "%d %d", &opt, &x );switch ( opt ) {case 1 : insert ( x ); break;case 2 : delet ( x ); break;case 3 : get_rank ( x ); break;case 4 : printf ( "%d\n", find_kth ( root, x ) ); break;case 5 : printf ( "%d\n", pre ( x ) ); break;case 6 : printf ( "%d\n", suf ( x ) ); break;}}return 0;
}

例题2：文艺线段树

题目

点击查看题目

代码实现

在这里因为涉及到一个区间翻转问题，我们就可以类比线段树打$lazy$标记，也对$treap$树打一个标记
那么在我们进行$split,merge$操作时，要保证对于一个点，它的左儿子和右儿子是对的，所以这里要写一个标记下放的$pushdown$
最后输出数列的时候也采用递归的方式，左中右的中序遍历，在这之间顺便进行标记下放

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 100005
#define INF 0x7f7f7f7f
int root, n, Size, m;
int son[MAXN][2], cnt[MAXN], siz[MAXN], rd[MAXN], key[MAXN];
bool lazy[MAXN];void push_up ( int x ) {siz[x] = siz[son[x][0]] + siz[son[x][1]] + cnt[x];
}void pushdown ( int x ) {if ( x && lazy[x] ) {swap ( son[x][0], son[x][1] );lazy[son[x][0]] = !lazy[son[x][0]];lazy[son[x][1]] = !lazy[son[x][1]];lazy[x] = 0;return; }
}void split ( int p, int &l, int &r, int x ) {if ( ! p ) {l = r = 0;return;}pushdown ( p );//千万不要放在if-else里面，先把标记下放去交换左右儿子//确保此时p的左右儿子是真的，不然就报错了/(ㄒoㄒ)/~~if ( siz[son[p][0]] + 1 <= x ) {l = p;split ( son[p][1], son[p][1], r, x - siz[son[p][0]] - 1 );push_up ( l );}else {r = p;split ( son[p][0], l, son[p][0], x );push_up ( r );}
}void merge ( int &p, int x, int y ) {if ( ! x || ! y ) {p = x + y;return;}if ( rd[x] < rd[y] ) {pushdown ( x );p = x;merge ( son[p][1], son[p][1], y );}else {pushdown ( y );p = y;merge ( son[p][0], x, son[p][0] );}push_up ( p );
}void insert ( int x ) {int l, r, L, R;split ( root, l, r, x );split ( l, L, R, x - 1 );if ( R ) {cnt[R] ++;push_up ( R );merge ( l, L, R );merge ( root, l, r );}else {++ Size;cnt[Size] = siz[Size] = 1;rd[Size] = rand ();key[Size] = x;merge ( l, L, Size );merge ( root, l, r );}
}void delet ( int x ) {int l, r, L, R;split ( root, l, r, x );split ( l, L, R, x - 1 );if ( R && cnt[R] > 1 ) {cnt[R] --;push_up ( R );merge ( l, L, R );merge ( root, l, r );}elsemerge ( root, L, r );
}void print ( int x ) {if ( ! x )return;pushdown ( x );print ( son[x][0] );printf ( "%d ", key[x] );print ( son[x][1] );
}void reverse ( int x, int y ) {int l, r, L, R;split ( root, l, r, y );split ( l, L, R, x - 1 );lazy[R] = !lazy[R];merge ( l, L, R );merge ( root, l, r );
}int main() {scanf ( "%d %d", &n, &m );for ( int i = 1;i <= n;i ++ )insert ( i );for ( int i = 1;i <= m;i ++ ) {int idl, idr;scanf ( "%d %d", &idl, &idr );reverse ( idl, idr );}print ( root );return 0;
}

因此这道题启示我们，随着我们的操作要求的不一样，在$split$和$merge$中一些语句可能会发生顺序变换，不能盲目地去背模板，一定要理解

可能会有部分代码细节错误，因为这些题实在是水，导致有些写错的代码还是能跑过数据

---