在讲一致性Hash之前我们先来讨论一个问题。

　　问题：现在有亿级用户，每日产生千万级订单，如何将订单进行分片分表？

　　小A：我们可以按照手机号的尾数进行分片，同一个尾数的手机号写入同一片/同一表中。

　　大佬：我希望通过会员ID来查询这个会员的所有订单信息，按照手机号分片/分表的话，前提是需要该用户的手机号保持不变，并且在查询订单列表时需要提前查询该用户的手机号，利用手机号尾数不太合理。

　　小B：按照大佬的思路，我们需要找出一个唯一不变的属性来进行分片/分表。

　　大佬：迷之微笑~

　　小B：（信心十足）会员在我们这边保持不变的就是会员ID（int），我们可以通过会员ID的尾数进行分片/分表

　　小C：尽然我们可以用会员ID尾数进行分片/分表，那就用取模的方式来进行分片/分表，通过取模的方式可以达到很好的平衡性。示意图如下：

 　　

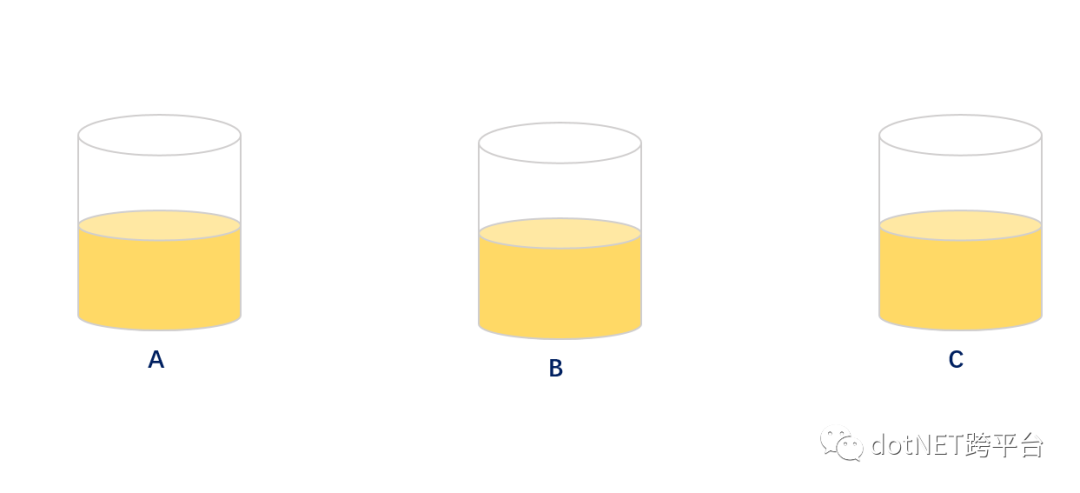
　　大佬：嗯嗯嗯，在不考虑会员冷热度的情况下小B和小C说的方案绝佳；但是往往我们的会员有冷热度和僵尸会员，通过取模的方式往往会出现某个分片数据异常高，部分分片数据异常低，导致平衡倾斜。示意图如下：

　　

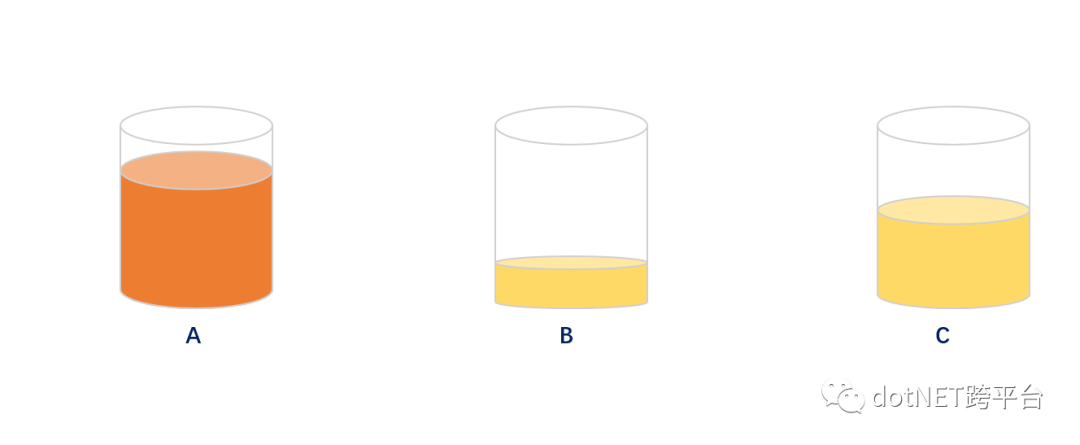
　　大佬：当出现某个分片/分表达到极限时我们需要添加片/表，此时发现我们无法正常添加片/表。因为一旦添加片/或表的时候会导致绝大部分数据错乱，按照原先的取模方式是无法正常获取数据的。示意图如下

　　

 

 

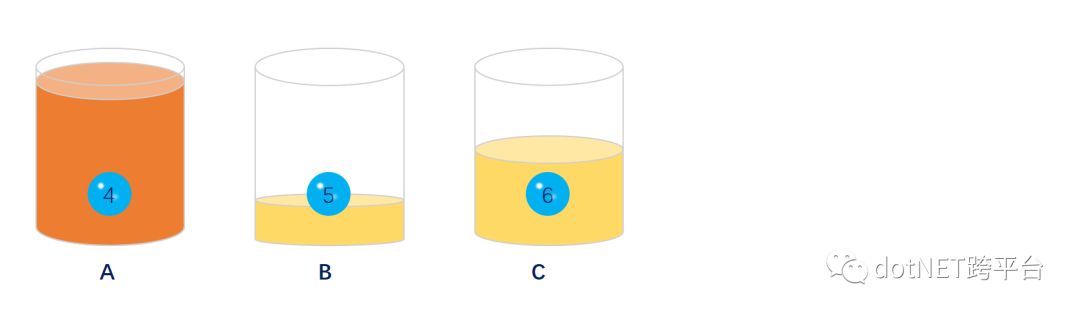
添加分片/分表前4,5,6会员的订单分别存储在A，B，C上，当添加了片/表的时候在按照（会员ID%N）方式取模去取数据4,5,6会员的订单数据时发现无法取到订单数据，因为此时4,5,6这三位会员数据分布存在了D，E，A上，具体示意图如下： 

　　

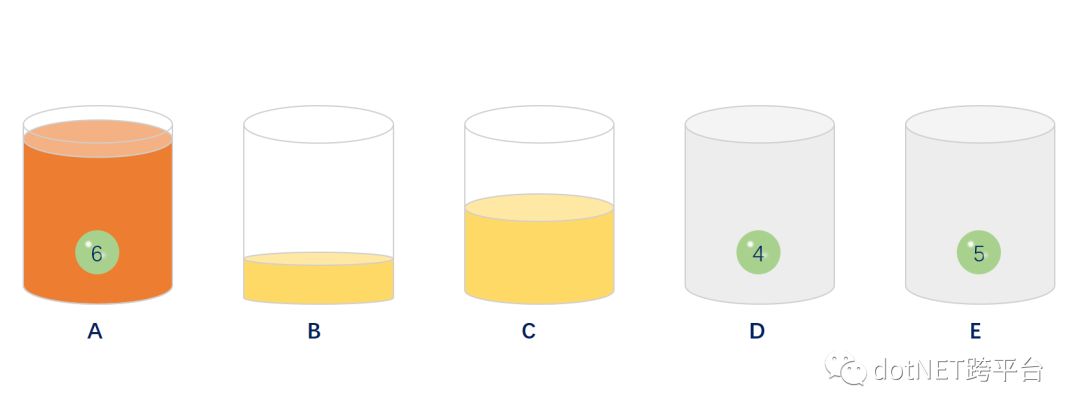
　　大佬：所以通过取模的方式也会存在缺陷；好了接下来我们来利用一致hash原理的方式来解决分片/分表的问题。

 首先什么是一致性哈希算法?一致性哈希算法(Consistent Hashing Algorithm)是一种分布式算法，常用于负载均衡。Memcached client也选择这种算法，解决将key-value均匀分配到众多Memcached server上的问题。它可以取代传统的取模操作，解决了取模操作无法应对增删Memcached Server的问题(增删server会导致同一个key,在get操作时分配不到数据真正存储的server，命中率会急剧下降)。

 　　还以上述问题为例，假如我们有10片，我们利用Hash算法将每一片算出一个Hash值，而这些Hash点将被虚拟分布在Hash圆环上，理论视图如下：　　

　　

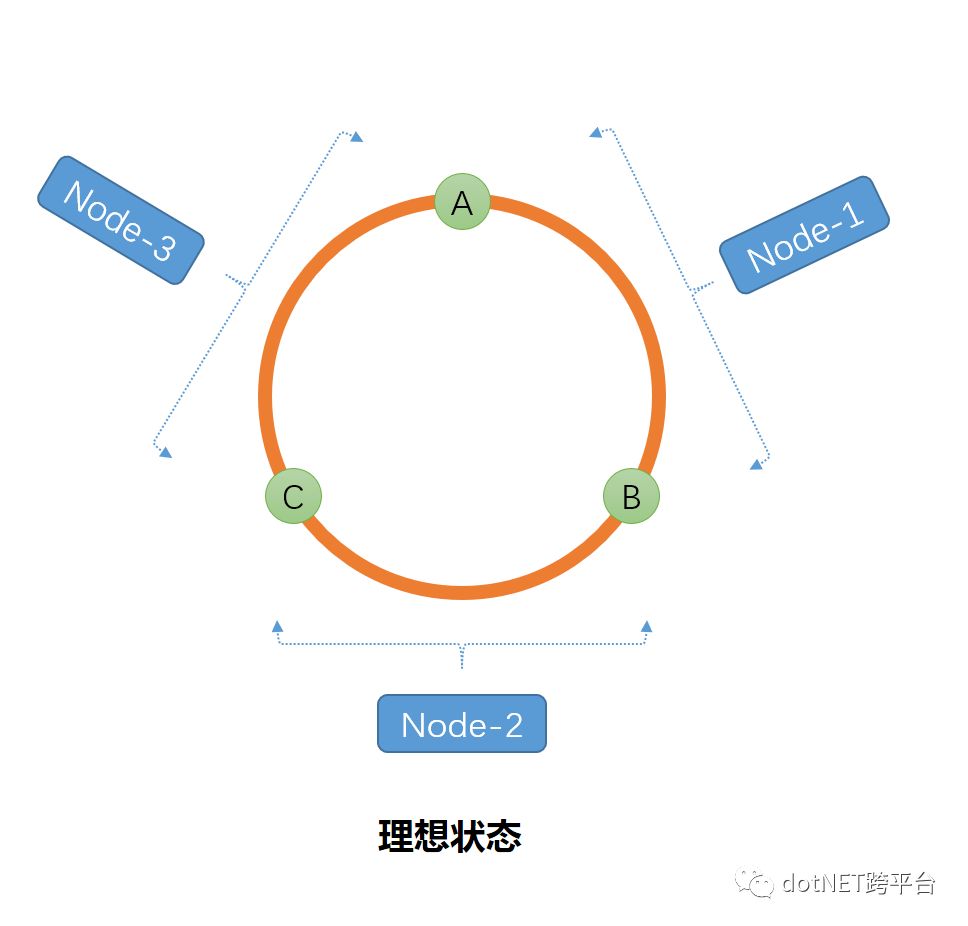
　　按照顺时针的方向，每个点与点之间的弧形属于每个起点片的容量，然后按照同样的Hash计算方法对每个会员ID进行Hash计算得出每个Hash值然后按照区间进行落片/表，以保证数据均匀分布。

如果此时需要在B和C之间新增一片/表(B1)的话，就不会出现按照取模形式导致数据几乎全部错乱的情况，仅仅是影响了(B1,C)之间的数据，这样我们清洗出来也就比较方便，也不会出现数据大批量

瘫痪。

　　但是如果我们仅仅是将片/表进行计算出Hash值之后，这些点分布并不是那么的均匀，比如就会下面的这种情况，导致区间倾斜。如图

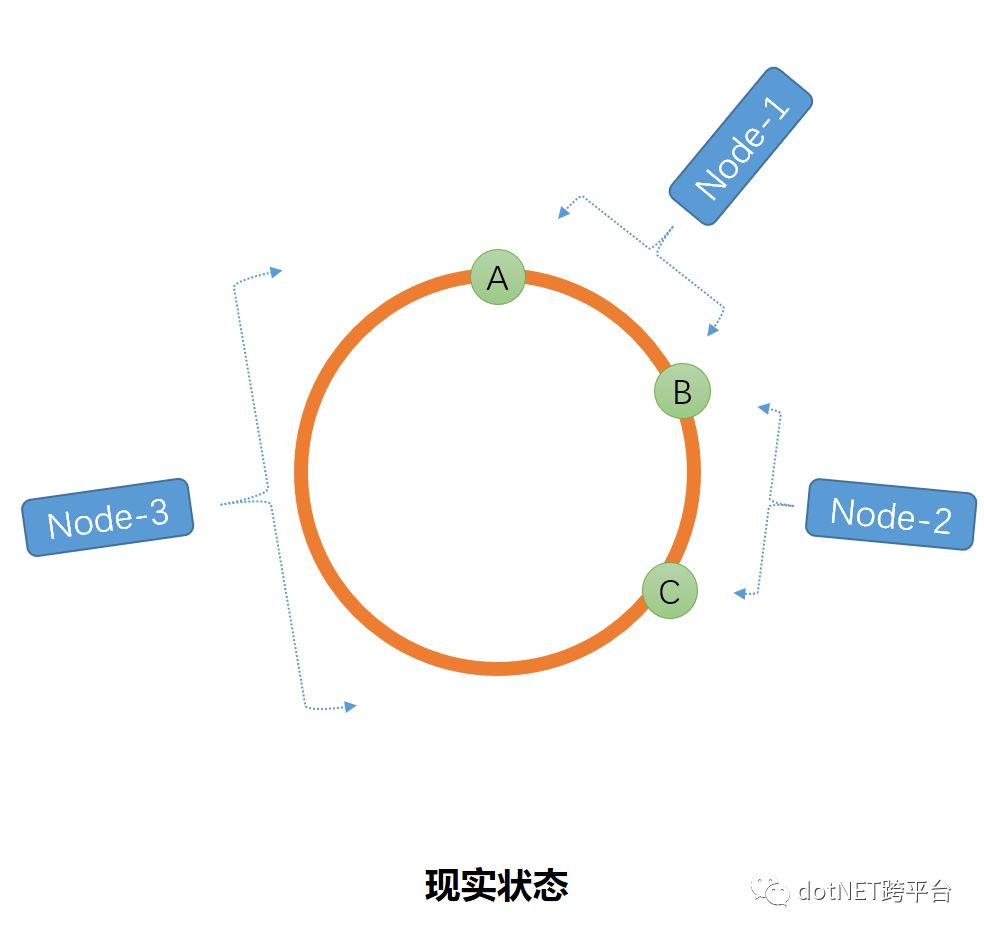
　　这个时候虚拟节点就此诞生，下面让我们来看一下虚拟节点在一致性Hash中的作用。当我们在Hash环上新增若干个点，那么每个点之间的距离就会接近相等。按照这个思路我们可以新增若干个

片/表，但是成本有限，我们通过复制多个A、B、C的副本({A1-An},{B1-Bn},{C1-Cn})一起参与计算，按照顺时针的方向进行数据分布，按照下图示意:

　　

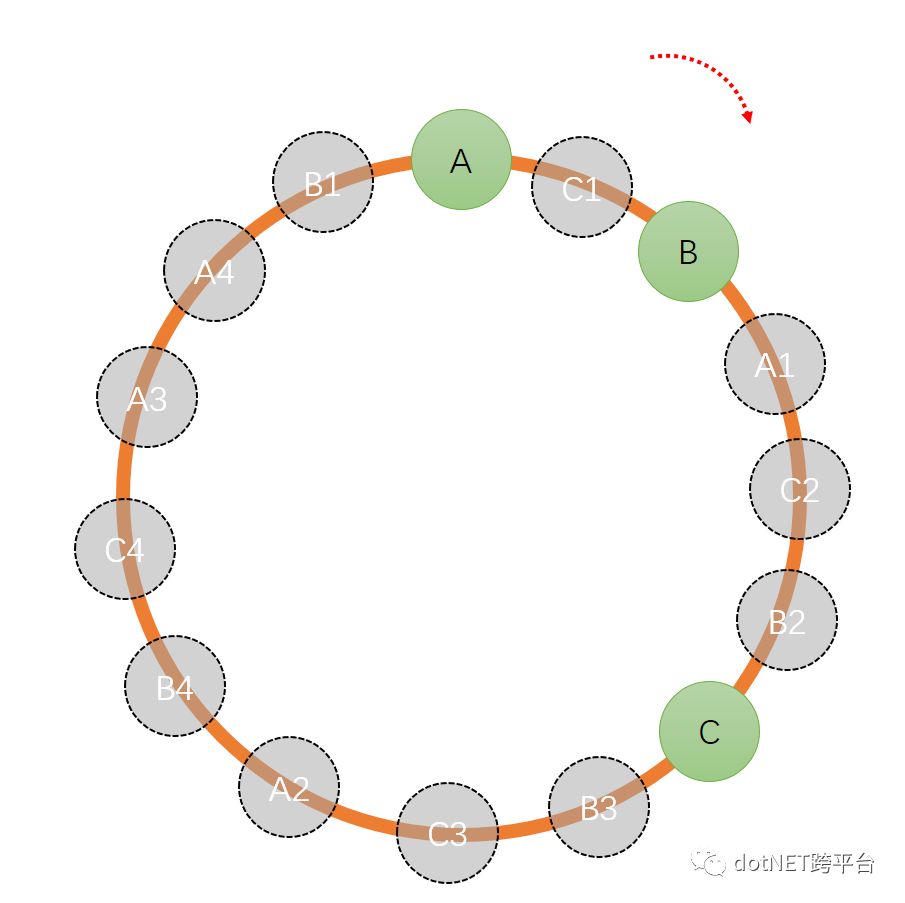
此时A=[A,C1)&[A1,C2)&[A2,B4)&[A3,A4)&[A4,B1)；B=[B,A1)&[B2,C)&[B3,C3)&[B4,C4)&[B1,A)；C=[C1,B)&[C2,B2)&[C,B3)&[B3,C3)&[C4,A3)；由图可以看出分布点越密集，平衡性约好。

using System;

using System.Collections.Generic;

using System.Data.HashFunction;

using System.Data.HashFunction.xxHash;

using System.Linq;

namespace HashTest

{

    public class ConsistentHash

    {

        /// <summary>

        /// 虚拟节点数

        /// </summary>

        private static readonly int VirturalNodeNum = 10;

        /// <summary>

        /// 服务器IP

        /// </summary>

        private static readonly string[] Nodes = { "192.168.1.1", "192.168.1.2", "192.168.1.3"};

        /// <summary>

        /// 按照一致性Hash进行分组

        /// </summary>

        private static readonly IDictionary<uint, string> ConsistentHashNodes = new Dictionary<uint, string>();

        private static uint[] _nodeKeys = null;

               

        public static void ComputeNode()

        {

            foreach (var node in Nodes)

            {

                AddNode(node);

            }

        }

        private static void AddNode(string node)

        {

            for (int i = 0; i < VirturalNodeNum; i++)

            {

                var key = node + ":" + i;

                var hashValue = ComputeHash(key);

                if (!ConsistentHashNodes.ContainsKey(hashValue))

                {

                    ConsistentHashNodes.Add(hashValue, node);

                }

            }

            _nodeKeys = ConsistentHashNodes.Keys.ToArray();

        }

        private static uint ComputeHash(string virturalNode)

        {

            var hashFunction = xxHashFactory.Instance.Create();

            var hashValue = hashFunction.ComputeHash(virturalNode);

            return BitConverter.ToUInt32(hashValue.Hash, 0);

        }

        public static string Get(string item)

        {

            var hashValue = ComputeHash(item);

            var index = GetClockwiseNearestNode(hashValue);

            return ConsistentHashNodes[_nodeKeys[index]];

        }

        private static int GetClockwiseNearestNode(uint hash)

        {

            int begin = 0;

            int end = _nodeKeys.Length - 1;

            if (_nodeKeys[end] < hash || _nodeKeys[0] > hash)

            {

                return 0;

            }

            while ((end - begin) > 1)

            {

                var mid = (end + begin) / 2;

                if (_nodeKeys[mid] >= hash) end = mid;

                else begin = mid;

            }

            return end;

        }

    }

}

原文地址：https://www.cnblogs.com/xialihua1023/p/10304932.html

---

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com