description

我们的小朋友很喜欢计算机科学，而且尤其喜欢二叉树。
考虑一个含有n个互异正整数的序列c[1],c[2],…,c[n]。如果一棵带点权的有根二叉树满足其所有顶点的权值都在集合{c[1],c[2],…,c[n]}中，我们的小朋友就会将其称作神犇的。并且他认为，一棵带点权的树的权值，是其所有顶点权值的总和。
给出一个整数m，你能对于任意的s(1<=s<=m)计算出权值为s的神犇二叉树的个数吗？请参照样例以更好的理解什么样的两棵二叉树会被视为不同的。
我们只需要知道答案关于998244353(7172^23+1,一个质数)取模后的值。
Input

第一行有2个整数 n,m(1<=n<=10^5; 1<=m<=10^5)。
第二行有n个用空格隔开的互异的整数 c[1],c[2],…,c[n]（1<=c[i]<=10^5)。
Output

输出m行，每行有一个整数。第i行应当含有权值恰为i的神犇二叉树的总数。请输出答案关于998244353(=7172^23+1,一个质数)取模后的结果。
Sample Input
样例一：
2 3
1 2
样例二：
3 10
9 4 3
样例三：
5 10
13 10 6 4 15
Sample Output
样例一：
1
3
9
样例二：
0
0
1
1
0
2
4
2
6
15
样例三：
0
0
0
1
0
1
0
2
0
5
Hint

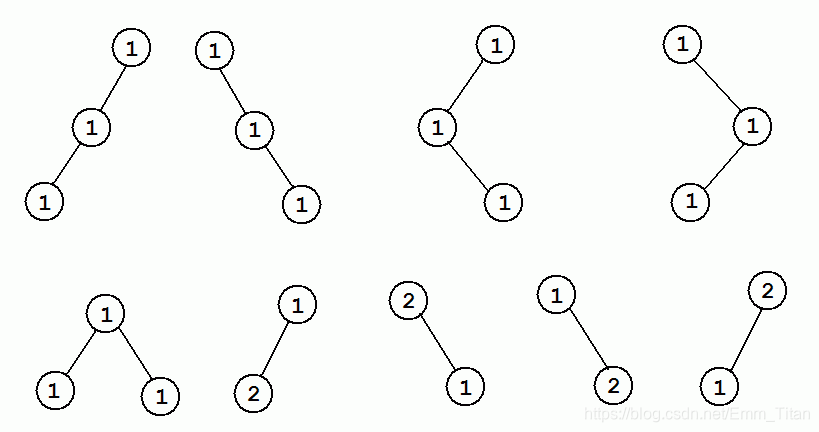
对于第一个样例，有9个权值恰好为3的神犇二叉树：

Source
VFleaKing & pyx1997 感谢wyl8899提供中文翻译

solution

取模俺就省略不写了
设$f[i]$：表示权值和为$i$的本质不同的子树个数
$g[i]$：表示子树根节点是否属于$|C|$
则可以通过枚举左右儿子及自己本身的权值，列出最暴力简单的状态转移方程
$$f_i=\sum _{j=0}^{i}g[j]\sum _{k=0}^{i-j}{f}_k{f}_{i-j-k}$$
这无非是一个卷积再卷积的形式，于是就跟生成函数沾边了
令$f$序列的生成函数为$F(x)$，$g$序列的生成函数为$G(x)$，则有
$$F=G\times F^2+1$$
加1是因为这个子树可能是只有根节点的
$$F=G\times F^2+1\iff G{F}^2-F+1=0\Rightarrow F=\frac{1\pm \sqrt{1-4G}}{2G}\Rightarrow F=\frac{1-\sqrt{1-4G}}{2G}$$
套上多项式开根与多项式求逆即可
是一道码农题

code

#include <cstdio>
#include <iostream>
using namespace std;
#define int long long
#define mod 998244353
#define maxn 300005
int inv2;
int r[maxn], c[maxn], v[maxn], ni[maxn];
int A[maxn], B[maxn], F[maxn], G[maxn];int qkpow( int x, int y ) {int ans = 1;while( y ) {if( y & 1 ) ans = ans * x % mod;x = x * x % mod;y >>= 1;}return ans;
}void NTT( int *h, int opt, int n ) {int len = 1, l = 0;while( len < n ) len <<= 1, l ++;for( int i = 0;i < len;i ++ )r[i] = ( r[i >> 1] >> 1 ) | ( ( i & 1 ) << ( l - 1 ) );for( int i = 0;i < len;i ++ ) if( i < r[i] ) swap( h[i], h[r[i]] );for( int i = 1;i < len;i <<= 1 ) {int omega = qkpow( opt == 1 ? 3 : mod / 3 + 1, ( mod - 1 ) / ( i << 1 ) );for( int j = 0;j < len;j += ( i << 1 ) )for( int k = 0, w = 1;k < i;k ++, w = w * omega % mod ) {int x = h[j + k], y = h[j + k + i] * w % mod;h[j + k] = ( x + y ) % mod;h[j + k + i] = ( x - y + mod ) % mod;}}if( opt == -1 ) {int inv = qkpow( len, mod - 2 );for( int i = 0;i < len;i ++ )h[i] = h[i] * inv % mod;}
}void polyinv( int n, int *f, int *g ) {if( n == 1 ) { g[0] = qkpow( f[0], mod - 2 ); return; }polyinv( ( n + 1 ) >> 1, f, g );for( int i = 0;i < n;i ++ ) A[i] = f[i], B[i] = g[i];NTT( A, 1, n << 1 );NTT( B, 1, n << 1 );for( int i = 0;i < ( n << 1 );i ++ ) A[i] = A[i] * B[i] % mod * B[i] % mod;NTT( A, -1, n << 1 );for( int i = 0;i < n;i ++ )g[i] = ( g[i] + g[i] - A[i] + mod ) % mod;for( int i = 0;i < ( n << 1 );i ++ ) A[i] = B[i] = 0;
}void polysqrt( int n, int *f, int *g ) {if( n == 1 ) { g[0] = 1; return; }polysqrt( ( n + 1 ) >> 1, f, g );for( int i = 0;i < n;i ++ ) F[i] = f[i];polyinv( n, g, G );NTT( F, 1, n << 1 );NTT( G, 1, n << 1 );for( int i = 0;i < ( n << 1 );i ++ ) G[i] = G[i] * F[i] % mod;NTT( G, -1, n << 1 );for( int i = 0;i < n;i ++ )g[i] = ( G[i] + g[i] ) % mod * inv2 % mod;for( int i = 0;i < ( n << 1 );i ++ ) F[i] = G[i] = 0;
}signed main() {inv2 = qkpow( 2, mod - 2 );int n, m;scanf( "%lld %lld", &n, &m );for( int i = 1, x;i <= n;i ++ ) {scanf( "%lld", &x );c[x] ++;}int len = 1;while( len <= m ) len <<= 1;for( int i = 0;i < len;i ++ )c[i] = mod - ( c[i] << 2 );c[0] ++;polysqrt( len, c, v );v[0] = ( v[0] + 1 ) % mod;polyinv( len, v, ni );for( int i = 1;i <= m;i ++ )printf( "%lld\n", ( ni[i] << 1 ) % mod );return 0;
}