H - Tunnel Warfare HDU - 1540

题意：

n个数顺序排列，左右数相连，
现在有三个操作：
1.摧毁一个位置上的数
2.回复上一次摧毁的数
3.查询包含该位置的最长连续区间长度

题解：

有两个方法，第一个是区间的最大值-最小值-1，这个就不讲了
第二个方法是区间合并更新答案
参考文章
利用线段树 求出每个线段左端点长度lsum（自左端点向右的连续长度），右端点长度rsum（自右端点向左连续长度） 以及区间内最长连续长度sum（以为可能存在一个连续长度既不包含左端点也不包含右端点）
破坏和修复的区别其实就是lsum，rsum，sum的值
我们用一个函数来求，1表示存在，0表示被破坏
详细讲讲过程：
如果区间合并更新答案？
我们已经定义了lsum，rsum，和sum
我们更新lsum，rsum，然后用来更新sum
如果左子树满了，root的lsum的长度就等于左子树（root<<1）的长度加上右子树(root<<1|1)的lsum

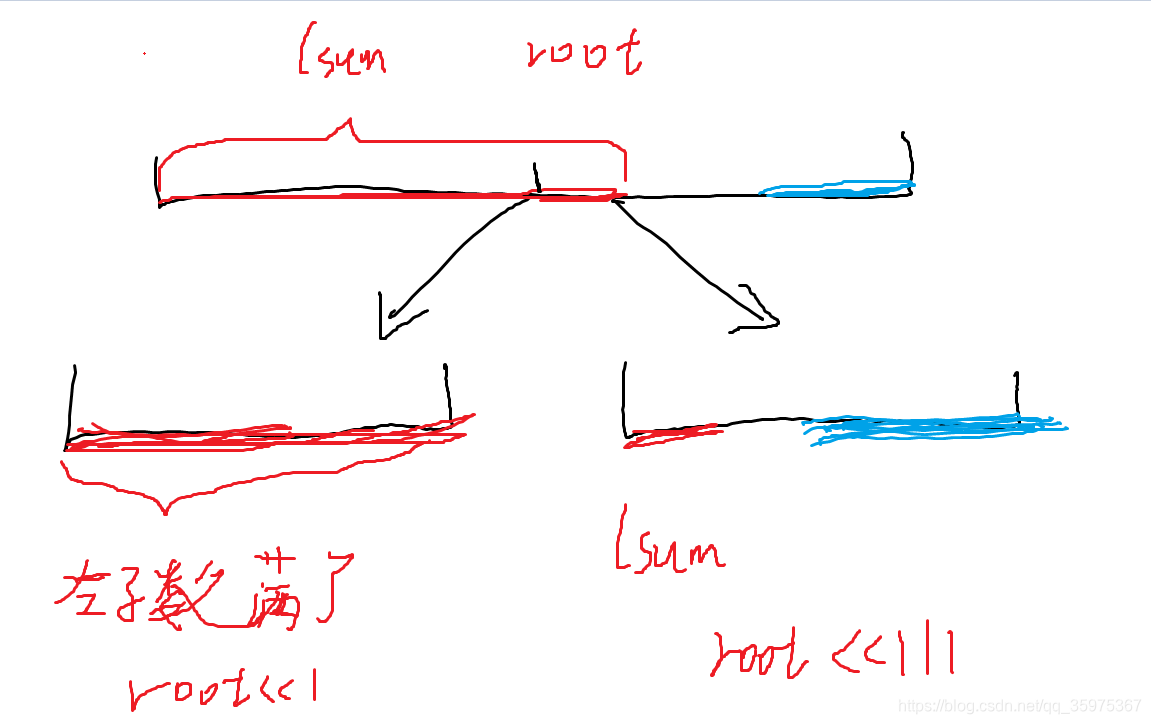
右子树同理
最长区间是三部分取最大值
1.左子树从左端点开始的最长连续区间
2.右子树从右端点开始的最长连续区间
（上面这俩就是刚才讲的更新）
3.左子树的右端点向左+右子树的左端点向右 （如图）

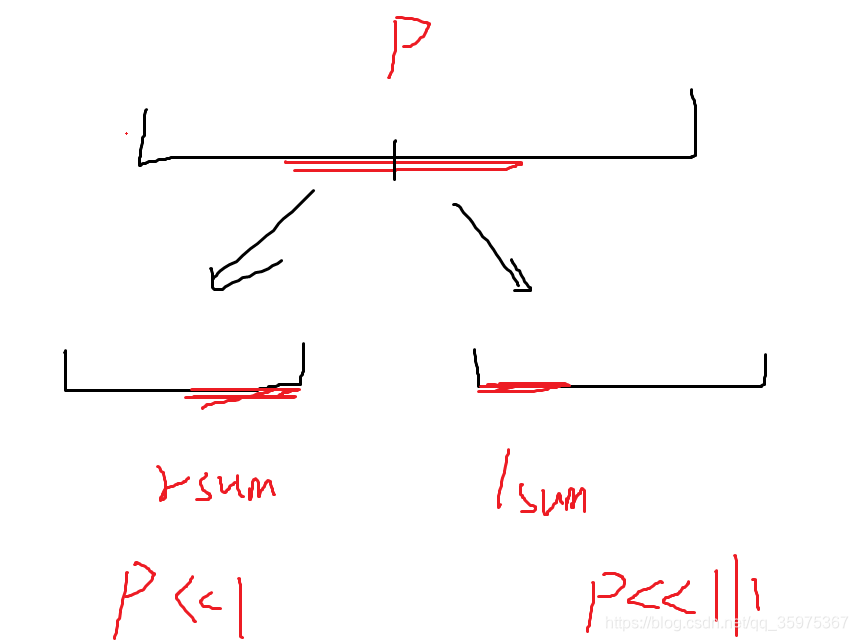
更新时就将lsum,rsum,sum更新为所指坐标，如果是摧毁就赋值为0
查询就是找点在哪个区间，输出答案就行

代码：

#include <iostream>
#include <bits/stdc++.h>
using namespace std;const int maxn = 50005;struct node {int L, R, lsum, rsum, sum;//左端点长度lsum（自左端点向右的连续长度）//区间内最长连续长度int Mid() {return (L+R)/2;}int Len() {return (R-L+1);}
}a[maxn*4];
void pushup(int p) {a[p].lsum = a[p << 1].lsum;a[p].rsum = a[p << 1|1].rsum;if (a[p << 1].lsum == a[p << 1].Len())//左子树满 a[p].lsum = a[p << 1].Len()+a[p << 1|1].lsum;if (a[p << 1|1].rsum == a[p << 1|1].Len())//右子树满 a[p].rsum =a[p << 1|1].Len()+a[p << 1].rsum;/*然后是三部分取最大值1.左子树从左端点开始的最长连续区间2.右子树从右端点开始的最长连续区间3.左子树的右端点向左+右子树的左端点向右 */int len=a[p<<1].rsum+a[p<<1|1].lsum;a[p].sum = max(a[p].lsum, max(a[p].rsum, len));
}void Build(int p, int l, int r) {a[p].L = l;a[p].R = r;a[p].lsum = a[p].rsum = a[p].sum = a[p].Len();if (l == r) return;Build(p << 1, l, a[p].Mid());Build(p << 1|1, a[p].Mid()+1, r);
}void Insert(int p, int k, int x) {if (a[p].L == a[p].R) {a[p].lsum = a[p].rsum = a[p].sum = x;return;}if (k <= a[p].Mid())Insert(p << 1, k, x);elseInsert(p << 1|1, k, x);pushup(p);
}int Query(int p, int k) {if (a[p].sum == 0) return 0;//先查看k是否被左右俩个区间包括在内 if (k < a[p].L+a[p].lsum) return a[p].lsum;if (k > a[p].R-a[p].rsum) return a[p].rsum;//然后查看左子树有部分+右子树左部分 if (k > a[p << 1].R-a[p << 1].rsum&&k < a[p << 1|1].L+a[p << 1|1].lsum)return a[p << 1].rsum+a[p << 1|1].lsum;if (k <= a[p].Mid())return Query(p << 1, k);elsereturn Query(p << 1|1, k);
}
int main() {int n, m;while (~scanf("%d%d", &n, &m)) {int x;char s[10];stack <int> sta;Build(1, 1, n);while (m--) {scanf("%s", s);if (s[0] == 'D') {scanf("%d", &x);Insert(1, x, 0);sta.push(x);} else if (s[0] == 'R'&&sta.size()) {Insert(1, sta.top(), 1);sta.pop();} else if (s[0] == 'Q') {scanf("%d", &x);printf("%d\n", Query(1, x));}}}return 0;
}