本文介绍Ocelot中的配置管理，配置管理允许在Api网关运行时动态通过Http Api查看/修改当前配置。由于该功能权限很高，所以需要授权才能进行相关操作。有两种方式来认证，外部Identity Server或内部Identity Server。

1、外部Identity Server

修改 Startup 中的 ConfigureServices 方法如下：

public void ConfigureServices(IServiceCollection services)
{
    services.AddMvc();

void options(IdentityServerAuthenticationOptions o)
{
        o.Authority = "http://localhost:6000";
        o.RequireHttpsMetadata = false;
        o.ApiName = "api1";
    }

    services
        .AddOcelot(new ConfigurationBuilder()
            .AddJsonFile("configuration.json")
            .Build())
        .AddAdministration("/administration", options);

    services             
      .AddAuthentication(JwtBearerDefaults.AuthenticationScheme)
      .AddIdentityServerAuthentication("TestKey", options);
}

其中复用了Identity Server的配置。

2、内部Identity Server

修改 Startup 中的 ConfigureServices 方法如下：

public void ConfigureServices(IServiceCollection services)
{
    services.AddMvc();

    services.AddOcelot(new ConfigurationBuilder()
        .AddJsonFile("configuration.json")
        .Build())
        .AddAdministration("/administration", "secret");

    services
        .AddAuthentication(JwtBearerDefaults.AuthenticationScheme)
        .AddIdentityServerAuthentication("TestKey", options =>
        {
            options.Authority = "http://localhost:6000";
            options.RequireHttpsMetadata = false;
            options.ApiName = "api1";
        });
}

其中为secret值为"secret"，后边会用得到。

其上为添加配置管理的两种方式，本例中以内部Identity Server为例。

Administration一共提供了3组Api

• Token获取

• 配置管理

• 缓存管理
  其中Token获取Api只在使用内部Identity Server时有效。由于缓存的教程还没更新，所以缓存管理的Api在后边的文章介绍。

1、Token获取

使用Postman请求http://localhost:5000/administration/connect/token如下所示，可以获得一个token

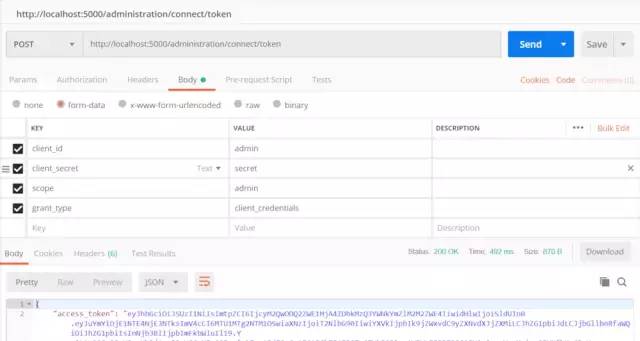
token from internal id server.png

注意Body的数据类型要选择 form-data，并且 client_secret 要填写代码中配置的secret，当前教程为secret。

2、配置管理

使用Postman请求http://localhost:5000/administration/configuration如下所示，获取配置

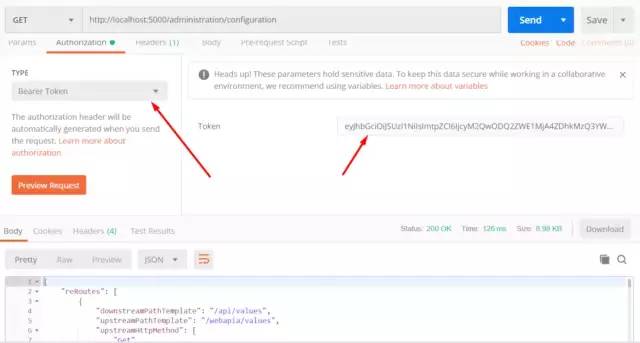
get configuration.png

使用上次获取的token。

以http://localhost:5000/GetUserInfo?name=Jonathan为例请求数据如下

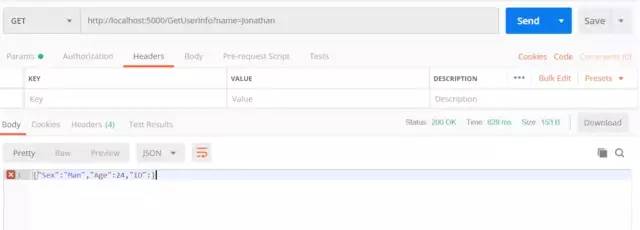
GetUserInfo.png

可以成功请求并且获取数据。

然后修改配置如下

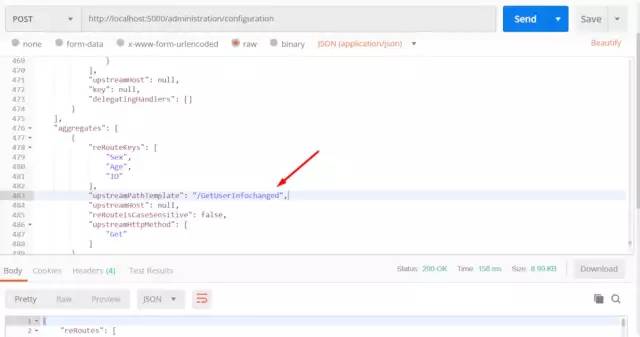
change configuration.png

注意此次请求为Post请求，并且不要忘记添加认证头token，此次请求的body参数为之前获取的配置并且修改了/GetUserInfo链接为/GetUserInfochanged。
再次使用Postman请求http://localhost:5000/GetUserInfo?name=Jonathan如下

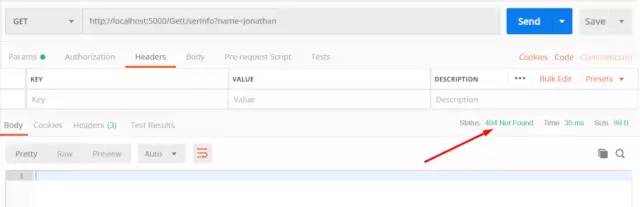
GetUserInfo 404.png

得到了404，修改链接为http://localhost:5000/GetUserInfochanged?name=Jonathan再次请求如下

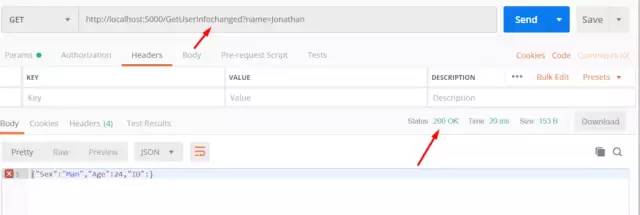
GetUserInfochanged.png

此次配置修改成功，打开到路径/OcelotTutorial/OcelotGetway/bin/Debug/netcoreapp2.0下有一个 configuration.Development.json 文件打开查看如下

configuration.Development.json.png

配置文件也已经修改。
可能在开发时会遇到修改完配置之后，下次调试时配置又回到了原来，是因为 configuration.json 选择成了总是复制，所以每次开始调试的时候都会替换 configuration.development.json 中的内容。
如果Ocelot Api网关程序没有读写文件的权限也会遇到修改配置失败的情况。

 

原文地址：https://www.jianshu.com/p/9e2fa5783211

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com