最大权闭合子图

content

先作出以下声明：

$c(u,v):$ 边 $(u,v)$ 的容量。

$f(u,v):$ 边 $(u,v)$ 的流量。

$[S,T]:$ 符号表示一个边集 $\{(u,v)|(u,v)\in E,u\in S,v\in T\}$。

$c[S,T]:$ 将流网络 $G=(V,E)$ 的点集划分成 $S,T(S+T=V)$ 两个完全不交的部分，源 $s\in S$，汇 $t\in T$，的割的容量。

容量最小的割即为一个网络的最小割。

问题引入：

一个有向图 $G=(V,E)$ 的闭合图 $G^{\prime }(V^{\prime },E^{\prime })$ 是原图的一个点集，且该点集的所有出边仍指向该点集。

即 ${\forall }_{(u,v)\in E},u\in V^{\prime }\Rightarrow v\in V^{\prime }$。

给每个点定义一个点权 $w$，最大权闭合图就是权和最大的闭合图，即最大化 ${\sum }_{v\in V^{\prime }}{w}_v$。

利用网络流的最小割进行快速求解，形式化的建图如下：

将图转化为网络 $N=(V_N,E_N)$，添入源点汇点 $s,t$。
{VN=V⋃{s,t}EN=E⋃{e=(s,v)∣v∈V,wv>0}⋃{e=(v,t)∣v∈V,wv<0}c(u,v)=∞e=(u,v)∈Ec(s,v)=wvwv>0c(v,t)=−wvwv<0\begin{cases} V_N=V\bigcup \{s,t\}\\ E_N=E\bigcup \{e=(s,v)|v\in V,w_v>0\}\bigcup\{e=(v,t)|v\in V,w_v<0\}\\ c(u,v)=∞\quad\quad e=(u,v)\in E\\ c(s,v)=w_v\quad \quad w_v>0\\ c(v,t)=-w_v\quad\ w_v<0 \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​VN​=V⋃{s,t}EN​=E⋃{e=(s,v)∣v∈V,wv​>0}⋃{e=(v,t)∣v∈V,wv​<0}c(u,v)=∞e=(u,v)∈Ec(s,v)=wv​wv​>0c(v,t)=−wv​ wv​<0​
定义：若一个 $s-t$ 割满足割中每条边都只与源点或汇点相连，则称该割为简单割。

根据定义可得，网络 $N$ 的简单割是不含原图 $G$ 中边集 $E$ 的任意一条边的。

• 引理1

  网络 $N$ 的最小割是简单割。

  证明：

  网络 $N$ 的边分为与源或汇关联，容量有限和不与源汇关联（原边集 $E$ 中所有边），容量无限的两种。

  所有与源或汇关联的边组成的割集的容量是有限的，为所有点权的绝对值和。

  最小割容量也至多为该绝对值和。

  故最小割不可能取任何容量为正无限的边，即最小割是简单割。

作出以下声明：

记简单割 $[S,T]$ 将网络 $N$ 的点集 $V_N$ 划分为点集 $S$ 及其补集 $T(T=V_N-S)$，且 $s\in S,t\in T$。

设闭合图为 $V_1$，则其在 $V$ 中补集为 $\overline{V_1}$。

记 $V^{+}$ 为 $V$ 中点权为正的点集，$V^{-}$ 为 $V$ 中点权为负的点集。

同样可以这么定义 $V_1^{+},V_1^{-},{\overline{V_1}}^{+},{\overline{V_1}}^{-}$。

• 引理2

  网络 $N$ 的简单割 $[S,T]$ 与图 $G$ 的闭合图 $V_1$ 存在一一对应的关系。
  即 V1⋃{s}=SV_1\bigcup \{s\}=SV1​⋃{s}=S。

  证明：

  • 闭合图对应简单割，即 S=V1⋃{s},V1ˉ⋃{t}S=V_1\bigcup\{s\},\bar{V_1}\bigcup\{t\}S=V1​⋃{s},V1​ˉ​⋃{t}。

    反证法。若存在 (u,v)∈E,u∈S−{s}=V1,v∈T−{t}=V1ˉ(u,v)\in E,u\in S-\{s\}=V_1,v\in T-\{t\}=\bar{V_1}(u,v)∈E,u∈S−{s}=V1​,v∈T−{t}=V1​ˉ​，使得 $[S,T]$ 含不与源汇关联的边。则闭合图 $V_1$ 有一个后继不在闭合图内，矛盾。

  • 简单割对应闭合图，即 V1=S−{s}V_1=S-\{s\}V1​=S−{s} 是闭合图。

    对于闭合图中 ${\forall }_{u\in V_1}$，考虑任意一条由 $u$ 引出的边 $(u,v)\in E$，由于简单割 $[S,T]$ 不含 $E$ 中任意一条边，所以 v≠T−{t}=V1ˉv\neq T-\{t\}=\bar{V_1}v​=T−{t}=V1​ˉ​。即 $v\in V_1$，符合闭合图定义。

• 推论

  $$c[S,T]=\sum _{v\in {\overline{V_1}}^{+}}{w}_v+\sum _{v\in V_1^{-}}(-w_v)$$

  证明：

  可以将割 $[S,T]$ 按照与源汇的关联分为三个部分:[S,T]=[{s},V1ˉ]⋃[{t},V1]⋃[V1,V1ˉ]:[S,T]=[\{s\},\bar{V_1}]\bigcup[\{t\},V_1]\bigcup[V_1,\bar{V_1}]:[S,T]=[{s},V1​ˉ​]⋃[{t},V1​]⋃[V1​,V1​ˉ​]。

  由于 $[S,T]$ 是简单割，所以 [$V_1,\overline{V_1}]=\varnothing$。

  因为源只与点权为正的点相连，所以 [{s},V1ˉ]=[{s},V1ˉ+][\{s\},\bar{V_1}]=[\{s\},\bar{V_1}^+][{s},V1​ˉ​]=[{s},V1​ˉ​+]。

  因为汇只与点权为负的点相连，所以 [{t},V1]=[{t},V1−][\{t\},V_1]=[\{t\},V_1^-][{t},V1​]=[{t},V1−​]。

• 定理

  当网络 $N$ 取最小割时，对应的闭合图达到最大权。

  证明：

  按照定义，闭合图的权和可以表示为：${\sum }_{v\in V_1^{+}}{w}_v-{\sum }_{v\in V_1^{-}}(-w_v)$。
  $$w(V_1)+c[S,T]=\sum _{v\in V_1^{+}}{w}_v-\sum _{v\in V_1^{-}}(-w_v)+\sum _{v\in {\overline{V_1}}^{+}}{w}_v+\sum _{v\in V_1^{-}}(-w_v)$$$$=\sum _{v\in V_1^{+}}{w}_v+\sum _{v\in {\overline{V_1}}^{+}}{w}_v=\sum _{v\in V^{+}}{w}_v$$
  即 $w(V_1)={\sum }_{v\in V^{+}}{w}_v-c[S,T]$。

  因为 ${\sum }_{v\in V^{+}}{w}_v$ 是原图 $G$ 中所有正权点之和，是常数。

  所以最大化闭合图权和，就得最小化简单割的容量，而最小割是简单割。得证。

复杂度就是求最小割的复杂度。

exercise

[NOI2006]最大获利

#include <bits/stdc++.h>
using namespace std;
#define maxn 60005
#define inf 0x7f7f7f7f
queue < int > q;
struct node { int to, nxt, flow; }E[maxn << 3];
int head[maxn], cur[maxn], dep[maxn];
int n, m, s, t, cnt;int read() {int x = 0; char s = getchar();while( s < '0' or s > '9' ) s = getchar();while( '0' <= s and s <= '9' ) {x = ( x << 1 ) + ( x << 3 ) + ( s ^ 48 );s = getchar();}return x;
}bool bfs() {memset( dep, 0, sizeof( dep ) );dep[s] = 1; q.push( s );while( ! q.empty() ) {int u = q.front(); q.pop();for( int i = cur[u] = head[u];~ i;i = E[i].nxt ) {int v = E[i].to;if( ! dep[v] and E[i].flow ) {dep[v] = dep[u] + 1;q.push( v );}}}return dep[t];
}int dfs( int u, int cap ) {if( u == t or ! cap ) return cap;int flow = 0;for( int i = cur[u];~ i;i = E[i].nxt ) {cur[u] = i; int v = E[i].to;if( dep[v] == dep[u] + 1 ) {int w = dfs( v, min( cap, E[i].flow ) );if( ! w ) continue;E[i ^ 1].flow += w;E[i].flow -= w;flow += w;cap -= w;if( ! cap ) break;}}return flow;
}int dinic() {int ans = 0;while( bfs() ) ans += dfs( s, inf );return ans;
}int id( int x, int y ) { return ( x - 1 ) * m + y; }bool inside( int x, int y ) {if( x < 1 or x > n or y < 1 or y > m ) return 0;return 1;
}void addedge( int u, int v, int w ) {E[cnt] = { v, head[u], w };head[u] = cnt ++;E[cnt] = { u, head[v], 0 };head[v] = cnt ++;
}int main() {memset( head, -1, sizeof( head ) );scanf( "%d %d", &n, &m );s = 0, t = n + m + 1;int sum = 0;for( int i = 1, x;i <= n;i ++ )addedge( s, i, x = read() );for( int i = 1;i <= m;i ++ ) {int a = read(), b = read(), c = read();addedge( a, i + n, inf );addedge( b, i + n, inf );addedge( i + n, t, c );sum += c;}sum -= dinic();printf( "%d\n", sum );return 0;
}

---

最大密度子图

content

问题引入：

给定一张图 $G=(V,E)$，从中选一个子图 $G^{\prime }=(V^{\prime },E^{\prime })$ 使得其密度 $D=\frac{|E^{\prime }|}{|V^{\prime }|}$ 最大。最大化并输出这个 $D$。

重新函数化上述式子：D=f(x)=∑e∈Exe∑v∈Vxv,x∈{0,1}D=f(x)=\frac{\sum_{e\in E}x_e}{\sum_{v\in V}x_v},x\in\{0,1\}D=f(x)=∑v∈V​xv​∑e∈E​xe​​,x∈{0,1}。

以下简记 $|V|=n,|E|=m$。

这个式子跟 0/1分数规划 有着异曲同工之妙。

同样考虑二分结果 $g$。

记：$h(g)={\max }_x\{{\sum }_{e\in E}{x}_e-{\sum }_{v\in V}{x}_v\ast g\}$。

记：问题最终答案为 $ans$，则 ${\forall }_{G^{\prime }=(n,m)}\frac{m}{n}\le ans$。
$$\{\begin{array}{l}h(g)=0\Rightarrow g=ans\\ h(g)>0\Rightarrow g<ans\\ h(g)<0\Rightarrow g>ans\end{array}$$
确定二分查找范围：$[\frac{1}{n},\frac{m}{1}]$。

确定精度误差：$\frac{1}{n^2}$。

• 引理1

  无向图 $G$ 中，任意两个具有不同密度的子图 $G_1,G_2$，其密度差不小于 $\frac{1}{n^2}$。

证明：

不妨假设 $G_1$ 子图的密度大于 $G_2$ 子图的密度。

$$\frac{m_1}{n_1}-\frac{m_2}{n_2}=\frac{m_1{n}_2-m_2{n}_1}{n_1{n}_2}\ge \frac{1}{n_1{n}_2}\ge \frac{1}{n^2}$$

• 推论

  对于无向图 $G$ 而言，如果存在密度为 $D$ 的子图 $G^{\prime }$，且不存在密度 $\ge D$ 的子图，则 $G^{\prime }$ 为最大密度子图。

---

接下来考虑如何求解二分答案对应的最大子图密度值 $h(g)$。

• 引理2

  当点集确定时，点集的诱导子图一定是最优解。

诱导子图：从原图 $G<V,E>$ 中选出一个子图 $G^{\prime }=(V^{\prime },E^{\prime })$，${\forall }_{u,v\in V^{\prime }}$ 必有 $e=(u,v)\in E^{\prime }$，即全选子图点集内部的边。

考虑假设点集被确定为 $V^{\prime }$，如何继续求解子图 $G^{\prime }=(V^{\prime },E^{\prime })$。

正向思维就是直接把点集中两两点之间的边选出来。但这里我们不采取这样的做法，因为暴力无法优化。

考虑逆向思维，将与点集 $V^{\prime }$ 相关的所有边集去除掉不是 $E^{\prime }$ 中的边集。

具体而言，用 ${\sum }_{v\in V^{\prime }}{d}_v-$ 红色边再除以 $2$，$d_i:i$ 点的度数。除以 $2$ 是因为 $E$ 的边被两个端点都算了一次。

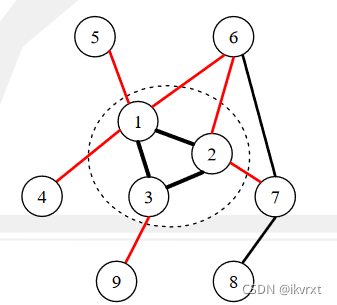
红色边的图上意义就是连接 $V$ 和 $V-V^{\prime }$ 两个完全不交的点集的边。

这就有一种「割」的意味了。

由于是要最大化 $|E^{\prime }|-g\cdot |V^{\prime }|$，乘以 $-1$ ，转化为最小化 $g\cdot |V^{\prime }|-|E^{\prime }|$。

$$g\cdot |V^{\prime }|-|E^{\prime }|=\sum _{v\in V^{\prime }}g-\sum _{e\in E^{\prime }}1=\sum _{v\in V^{\prime }}g-\frac{{\sum }_{v\in V^{\prime }}{d}_v-c[V^{\prime },V-V^{\prime }]}{2}$$$$=\frac{1}{2}(\sum _{v\in V^{\prime }}(2g-d_v)+c[V^{\prime },V-V^{\prime }])$$

${\sum }_{v\in V^{\prime }}(2g-d_v)$，就是选了 $v$，就要花费代价 $2g-d_v$， 这相当于每个点多了个 $2g-d_v$ 的点权。

常见处理，让 $V^{\prime }$ 中的点都与 $t$ 相连，把点权赋成边权。

由于最小割只接受非负边权，但点权可能为负数，那么就把所有边权都加上一个极大值 $Big$，保证非负，最后再减去即可。

总结，形式化地将图 $G=(V,E)$ 转化为网络 $N=(V_N,E_N)$：
{VN=V⋃{s,t}EN={(u,v)∣(u,v)∈E}⋃{(s,v)∣v∈V}⋃{(v,t)∣v∈V}c(u,v)=1(u,v)∈Ec(s,v)=Bigv∈Vc(v,t)=Big+2g−dvv∈V\begin{cases}V_N=V\bigcup\{s,t\}\\E_N=\{(u,v)|(u,v)\in E\}\bigcup\{(s,v)|v\in V\}\bigcup\{(v,t)|v\in V\}\\c(u,v)=1\quad\quad\quad\quad\quad\quad(u,v)\in E\\c(s,v)=Big\quad\quad\quad\quad\quad\ v\in V\\c(v,t)=Big+2g-d_v\quad v\in V\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧​VN​=V⋃{s,t}EN​={(u,v)∣(u,v)∈E}⋃{(s,v)∣v∈V}⋃{(v,t)∣v∈V}c(u,v)=1(u,v)∈Ec(s,v)=Big v∈Vc(v,t)=Big+2g−dv​v∈V​

• 引理3

  网络 $N$ 的一个割 $[S,T]$ 与原图 $G$ 的子图 $G^{\prime }=(V^{\prime },E^{\prime })$ 方案存在一一对应关系。即 V′⋃{s}=SV'\bigcup\{s\}=SV′⋃{s}=S。

  因为割可以是任意划分的，子图也可以是任意划分的。

• 定理

  网络 $N$ 的一个最小割 $[S,T]$ ，其根据 引理2 所对应子图 $G^{\prime }$ 是 $h(g)$ 的一个最优解。

  证明：

  设 $c[S,T]$ 为网络 $N$ 的任意一个割的容量。根据 引理3 V’=S−{s},V′ˉ=T−{t}V’=S-\{s\},\bar{V'}=T-\{t\}V’=S−{s},V′ˉ=T−{t}。
  $$c[S,T]=\sum _{u\in S,v\in T}c(u,v)=\sum _{v\in \overline{V^{\prime }}}c(s,v)+\sum _{v\in V^{\prime }}c(v,t)+\sum _{u\in V^{\prime },v\in \overline{V^{\prime }},(u,v)\in E}c(u,v)$$$$=\sum _{v\in \overline{V^{\prime }}}Big+\sum _{v\in V^{\prime }}Big+2g-d_v+\sum _{u\in V^{\prime },v\in \overline{V^{\prime }},(u,v)\in E}1$$$$=Big\cdot |V|+\sum _{u\in V^{\prime }}(2g-d_u+\sum _{v\in \overline{V^{\prime }},(u,v)\in E}1)$$$$=Big\cdot |V|+\sum _{u\in V^{\prime }}(2g-\sum _{v\in V^{\prime },(u,v)\in E}1)$$$$=Big\ast n+2g|V^{\prime }|-2|E^{\prime }|$$$$=U\ast n-2(|E^{\prime }|-g|V^{\prime }|)$$
  $E^{\prime }$ 已重定义为 $V^{\prime }$ 的导出子图的边集。

  $U\ast n$ 为定值，当割取最小的时候，$2(|E^{\prime }|-g|V^{\prime }|)$ 取最大。即 $h(g)=\frac{U\ast n-c[S,T]}{2}$，其中 $[S,T]$ 为最小割。

参考选摘：胡伯涛《最小割模型在信息学竞赛中的应用》

exercise

UVA Hard Life

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define maxn 100005
struct node { int to, nxt; double flow; }E[maxn];
struct Node { int u, v; }edge[maxn];
queue < int > q;
int n, m, s, t, cnt;
int head[maxn], cur[maxn], dep[maxn], d[maxn];
bool vis[maxn];void addedge( int u, int v, double w1, double w2 ) {E[cnt] = { v, head[u], w1 };head[u] = cnt ++;E[cnt] = { u, head[v], w2 };head[v] = cnt ++;
}void build( double g ) {memset( head, -1, sizeof( head ) ); cnt = 0;for( int i = 1;i <= m;i ++ ) addedge( edge[i].u, edge[i].v, 1, 1 );for( int i = 1;i <= n;i ++ ) addedge( s, i, m, 0 ), addedge( i, t, m + 2 * g - d[i], 0 );
}bool bfs() {memset( dep, 0, sizeof( dep ) );dep[s] = 1; q.push( s );while( ! q.empty() ) {int u = q.front(); q.pop();for( int i = cur[u] = head[u];~ i;i = E[i].nxt ) {int v = E[i].to;if( ! dep[v] and E[i].flow > 0 ) {dep[v] = dep[u] + 1;q.push( v );}}}return dep[t];
}double dfs( int u, double cap ) {if( u == t or cap <= 0 ) return cap;double flow = 0;for( int i = cur[u];~ i;i = E[i].nxt ) {cur[u] = i; int v = E[i].to;if( dep[v] == dep[u] + 1 ) {double w = dfs( v, min( cap, E[i].flow ) );if( w <= 0 ) continue;E[i ^ 1].flow += w;E[i].flow -= w;flow += w;cap -= w;if( cap <= 0 ) break;}}return flow;
}double dinic( double g ) {build( g );double ans = 0;while( bfs() ) ans += dfs( s, 2e9 );return ans;
}void dfs( int now ) {if( vis[now] ) return;vis[now] = 1;if( now ^ s ) cnt ++;for( int i = head[now];~ i;i = E[i].nxt )if( E[i].flow > 0 ) dfs( E[i].to );
}int main() {while( ~ scanf( "%d %d", &n, &m ) ) {s = 0, t = n + 1;for( int i = 0;i <= n;i ++ ) vis[i] = d[i] = 0;for( int i = 1, u, v;i <= m;i ++ ) {scanf( "%d %d", &u, &v );edge[i] = { u, v };d[u] ++, d[v] ++;}double l = 0, r = m, eps = 1.0 / double(n * n);while( r - l > eps ) {double mid = ( l + r ) / 2;if( m * n - dinic( mid ) > eps ) l = mid;else r = mid;}dinic( l );cnt = 0;dfs( s );if( ! cnt ) printf( "1\n1\n" );else {printf( "%d\n", cnt );for( int i = 1;i <= n;i ++ )if( vis[i] ) printf( "%d\n", i );}}return 0;
}

Upd：最大权闭合子图易懂证明