解析

Atcoder的题超小的码量总让人做不出来的时候感到很不甘心…
但这题确实挺难的，主要还是魔术一样的奇淫技巧。

大力推式子那个阴间方法我直接选择弃疗。
一个很显然的结论是：肯定回答当前剩的比较多的选项。

pia一张洛谷的图：

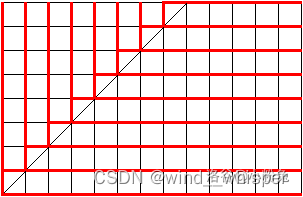
（来源：https://www.luogu.com.cn/blog/PinkRabbit/solution-at2705）

不失一般性的，令 $n>m$。
红色线表示我在每一个状态所作出的猜测，当折线走向和红线重合时，说明猜测正确，得一分。
那么我们只需要求出所有折线的得分和即可。
这咋算啊…
考虑一条折线，如果有任意部分到了途中的对角线上方，我们就直接把它折下来。
这样所有折线都始终在对角线下方了，那么得分显然是 $n$。
然而这题显然固输 $n$ 是过不去的。
因为我们少算了从对角线往左走那部分获得的贡献。但这部分的贡献也非常好算，用所有经过对角线各个位置的方案之和除以2即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define LL __int128
#define ull unsigned long long
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define ok debug("OK\n")
using namespace std;const int N=1e6+100;
const int mod=998244353;
inline ll read(){ll x(0),f(1);char c=getchar();while(!isdigit(c)) {if(c=='-')f=-1;c=getchar();}while(isdigit(c)) {x=(x<<1)+(x<<3)+c-'0';c=getchar();}return x*f;
}inline ll ksm(ll x,ll k){ll res(1);while(k){if(k&1) res=res*x%mod;x=x*x%mod;k>>=1;}return res;
}
int n,m;
ll jc[N],ni[N];
void init(int n){jc[0]=1;for(int i=1;i<=n;i++) jc[i]=jc[i-1]*i%mod;ni[n]=ksm(jc[n],mod-2);for(int i=n-1;i>=0;i--) ni[i]=ni[i+1]*(i+1)%mod;return;
}
inline ll C(int n,int m){return jc[n]*ni[m]%mod*ni[n-m]%mod;
}signed main(){#ifndef ONLINE_JUDGEfreopen("a.in","r",stdin);freopen("a.out","w",stdout);#endifint n=read(),m=read();if(n<m) swap(n,m);init(n+m);ll ans(0);for(int i=1;i<=m;i++){(ans+=C(i+i,i)*C(n-i+m-i,n-i))%=mod;}  ans=ans*(mod+1)/2%mod;ans=ans*ksm(C(n+m,n),mod-2)%mod;(ans+=n)%=mod;printf("%lld\n",ans);return 0;
}