problem

给定一棵 $n$ 个结点的无根树，每条边的边权均为 $1$ 。

树上标记有 $m$ 个互不相同的关键点，小 A 会在这 $m$ 个点中等概率随机地选择 $k$ 个不同的点放上小饼干。

你想知道，经过有小饼干的 $k$ 个点的最短路径长度的期望是多少。

注意，你可以任意选取起点和终点，路径也可以经过重复的点或重复的边。

答案对 $998244353$ 取模。

solution

observation ：起点和终点一定是有小饼干的特殊点。

因为要到达所有有小饼干的点，所以所有边都会走两次，除了起终点之间的路径只会走一次。

对这棵树建立虚树【只是在思想时体现，并不会在代码里体现】。

那么最短路径过程就是 dfs 虚树的过程，则可以表示为相邻两个小饼干点之间的路径之和的两倍➖一条路径的长度。

由于最短路径，可变的只有“一条路径的长度”选取，所以肯定是选最长的直径。

紧接着，发现这两个部分是独立的，可以分开计算。

• 考虑一条边在怎么的小饼干选取条件下会被纳入最短路径内计算。

  

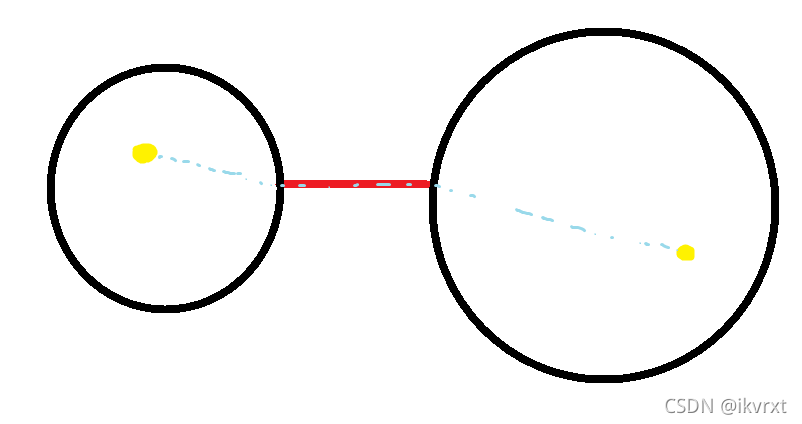
  显然，一条边将树划分成两个部分，当且仅当左右两个部分都有小饼干时才会计算到这条边的贡献。

  考虑左右两边都有小饼干的情况数。

  设左边部分大小为 $x$，则右边部分大小为 $n-x$【大小指的是点数】。

  数量为 $\left(\genfrac{}{}{0ex}{}{m}{k}\right)-\left(\genfrac{}{}{0ex}{}{x}{k}\right)-\left(\genfrac{}{}{0ex}{}{n-x}{k}\right)$【所有情况数减去全都在左边或全都在右边的不合法数】。

• 考虑一条路径【路径的两端 $u,v$ 一定是特殊的小饼干点】在怎样的小饼干选取条件下会被当成直径。

  显然，充要条件是：所有的小饼干点两两之间的距离不超过该路径长度。

  由于直径的性质【不断扩点更新直径的做法】只需要判断其余小饼干点到 $u,v$ 的距离都不超过考虑路径的长度。

  但是，很有可能有些小饼干分配方案，直径不是唯一的。

  这样就会因为“不超过”而被算重。

  所以需要对相同长度的直径指定一个规则，使之变为严格小于。

  这里选择最简单的一种：按照端点的编号排大小。

  注意：端点编号大小是第二关键字，使用这种方法排序的前提是第一关键字长度的大小相等。

  这样就会归纳出，这条路径是唯一的直径，当且仅当以下所有条件都不满足

  • $dis(u,v)<dis(u,i)$
  • $dis(u,v)<dis(v,i)$
  • $dis(u,v)=dis(u,i)\wedge i<v$
  • $dis(u,v)=dis(v,i)\wedge i<u$

枚举 $i$ 算出满足以上条件任何之一的 $i$ 的数量 $cnt$，最后就是计算剩下的 $k-2$ 个小饼干落到除去这些不合法点的情况数，即 $\left(\genfrac{}{}{0ex}{}{m-2-cnt}{k-2}\right)$。

最后所有贡献和除以总方案数 $\left(\genfrac{}{}{0ex}{}{m}{k}\right)$ 就是期望了。

时间复杂度 $O(m^3)$。

code

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define mod 998244353
#define maxn 2005
vector < int > G[maxn];
int c[maxn][maxn], dis[maxn][maxn], f[maxn][15];
int siz[maxn], a[maxn], dep[maxn];
int n, m, k, ans;void init() {for( int i = 0;i <= m;i ++ ) {c[i][0] = c[i][i] = 1;for( int j = 1;j < i;j ++ )c[i][j] = ( c[i - 1][j - 1] + c[i - 1][j] ) % mod;}
}void dfs( int u, int fa ) {f[u][0] = fa, dep[u] = dep[fa] + 1;for( int i = 1;i < 15;i ++ ) f[u][i] = f[f[u][i - 1]][i - 1];for( int v : G[u] ) if( v ^ fa ) {dfs( v, u );ans = ( ans + c[m][k] - c[siz[v]][k] - c[m - siz[v]][k] ) % mod;siz[u] += siz[v];}
}int lca( int u, int v ) {if( dep[u] < dep[v] ) swap( u, v );for( int i = 14;~ i;i -- ) if( dep[f[u][i]] >= dep[v] ) u = f[u][i];if( u == v ) return u;for( int i = 14;~ i;i -- ) if( f[u][i] ^ f[v][i] ) u = f[u][i], v = f[v][i];return f[u][0];
}int qkpow( int x, int y ) {int ans = 1;while( y ) {if( y & 1 ) ans = ans * x % mod;x = x * x % mod;y >>= 1;}return ans;
}signed main() {freopen( "tree.in", "r", stdin );freopen( "tree.out", "w", stdout );scanf( "%lld %lld %lld", &n, &m, &k );init(); for( int i = 1;i <= m;i ++ ) scanf( "%lld", &a[i] ), siz[a[i]] = 1;for( int i = 1, u, v;i < n;i ++ ) {scanf( "%lld %lld", &u, &v );G[u].push_back( v );G[v].push_back( u );}dfs( 1, 0 );ans = ans << 1; //一条边要走两次for( int i = 1;i <= m;i ++ )for( int j = i + 1;j <= m;j ++ )dis[i][j] = dis[j][i] = dep[a[i]] + dep[a[j]] - ( dep[lca( a[i], a[j] )] << 1 );for( int u = 1;u <= m;u ++ )for( int v = u + 1;v <= m;v ++ ) {int cnt = 0;for( int i = 1;i <= m;i ++ )if( i ^ u and i ^ v )cnt += dis[u][v] < max( dis[u][i], dis[v][i] ) or ( dis[u][v] == dis[i][v] and i < u ) or ( dis[u][v] == dis[i][u] and i < v );ans = ( ans - dis[u][v] * c[m - 2 - cnt][k - 2] ) % mod;}printf( "%lld\n", ( ans * qkpow( c[m][k], mod - 2 ) % mod + mod ) % mod );return 0;
}