H - Square Card HDU - 7063

题意：

有两个圆形区域，一个是得分区域，一个是获得奖金区域，现在你有一个边长为a的正方形,当正方形在如果在某一时刻它严格在圆形范围内，才算合法。
问把牌扔到任意的位置被得分和同时获得奖金的可能性与被得分的可能性的比率是多少

题解：

我第一反应是想直接rand得结果，突然发现想多了，其实就是求两个圆相交面积再比得分区域面积就行。但是注意题目要求牌必须完全在园内，也就是圆心所在位置并不是整个圆，而是比圆小一圈的情况，所以需要求新的半径

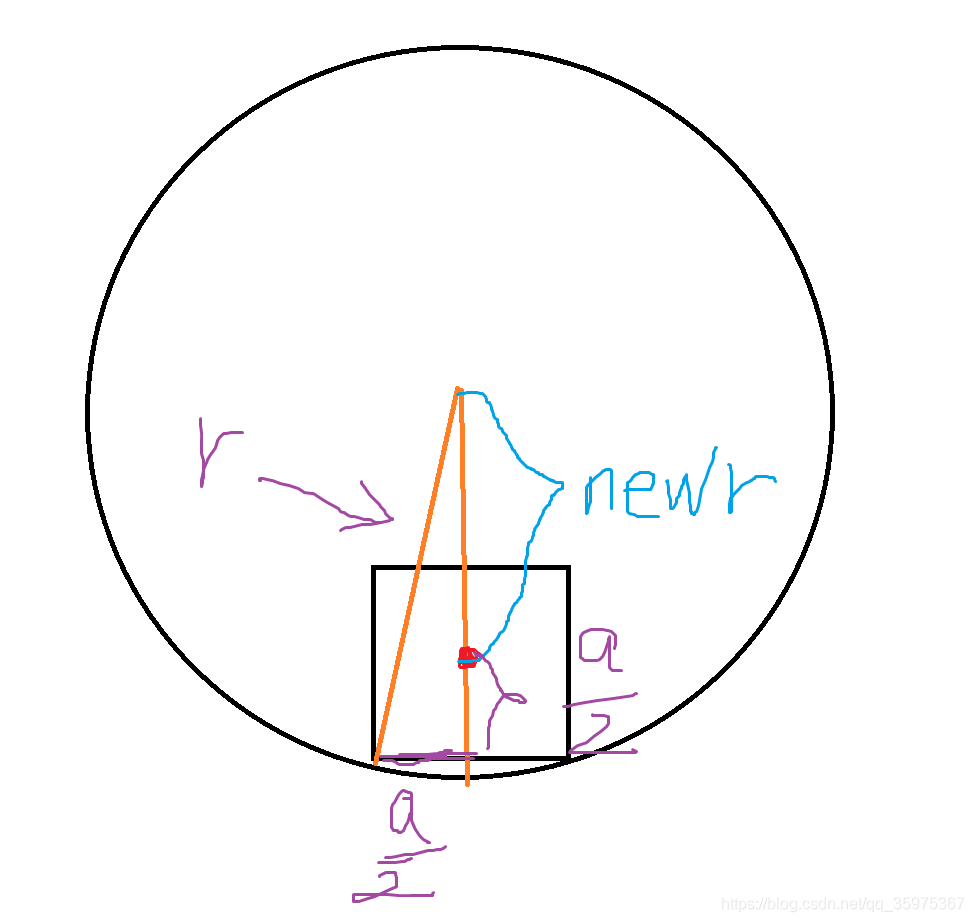
newr=sqrt(rr-aa/4)-a/2
求出两个新的r，然后相交求圆面积，做比就是结果

代码：

#include <bits/stdc++.h>
#include <unordered_map>
#define debug(a, b) printf("%s = %d\n", a, b);
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
clock_t startTime, endTime;
//Fe~Jozky
const ll INF_ll= 1e18;
const int INF_int= 0x3f3f3f3f;
template <typename T> inline void read(T& x)
{T f= 1;x= 0;char ch= getchar();while (0 == isdigit(ch)) {if (ch == '-')f= -1;ch= getchar();}while (0 != isdigit(ch))x= (x << 1) + (x << 3) + ch - '0', ch= getchar();x*= f;
}
template <typename T> inline void write(T x)
{if (x < 0) {x= ~(x - 1);putchar('-');}if (x > 9)write(x / 10);putchar(x % 10 + '0');
}
void rd_test()
{
#ifdef ONLINE_JUDGE
#elsestartTime= clock();freopen("in.txt", "r", stdin);
#endif
}
void Time_test()
{
#ifdef ONLINE_JUDGE
#elseendTime= clock();printf("\nRun Time:%lfs\n", (double)(endTime - startTime) / CLOCKS_PER_SEC);
#endif
}
// `计算几何模板`
const double eps= 1e-8;
const double inf= 1e20;
const double pi= acos(-1.0);
const int maxp= 1010;
//`Compares a double to zero`
int sgn(double x)
{if (fabs(x) < eps)return 0;if (x < 0)return -1;elsereturn 1;
}
//square of a double
inline double sqr(double x)
{return x * x;
}
/** Point* Point()               - Empty constructor* Point(double _x,double _y)  - constructor* input()             - double input* output()            - %.2f output* operator ==         - compares x and y* operator <          - compares first by x, then by y* operator -          - return new Point after subtracting curresponging x and y* operator ^          - cross product of 2d points* operator *          - dot product* len()               - gives length from origin* len2()              - gives square of length from origin* distance(Point p)   - gives distance from p* operator + Point b  - returns new Point after adding curresponging x and y* operator * double k - returns new Point after multiplieing x and y by k* operator / double k - returns new Point after divideing x and y by k* rad(Point a,Point b)- returns the angle of Point a and Point b from this Point* trunc(double r)     - return Point that if truncated the distance from center to r* rotleft()           - returns 90 degree ccw rotated point* rotright()          - returns 90 degree cw rotated point* rotate(Point p,double angle) - returns Point after rotateing the Point centering at p by angle radian ccw*/
struct Point
{double x, y;Point(){}Point(double _x, double _y){x= _x;y= _y;}void input(){scanf("%lf%lf", &x, &y);}void output(){printf("%.2f %.2f\n", x, y);}bool operator==(Point b) const{return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;}bool operator<(Point b) const{return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;}Point operator-(const Point& b) const{return Point(x - b.x, y - b.y);}//叉积double operator^(const Point& b) const{return x * b.y - y * b.x;}//点积double operator*(const Point& b) const{return x * b.x + y * b.y;}//返回长度double len(){return hypot(x, y); //库函数}//返回长度的平方double len2(){return x * x + y * y;}//返回两点的距离double distance(Point p){return hypot(x - p.x, y - p.y);}Point operator+(const Point& b) const{return Point(x + b.x, y + b.y);}Point operator*(const double& k) const{return Point(x * k, y * k);}Point operator/(const double& k) const{return Point(x / k, y / k);}//`计算pa  和  pb 的夹角`//`就是求这个点看a,b 所成的夹角`//`测试 LightOJ1203`double rad(Point a, Point b){Point p= *this;return fabs(atan2(fabs((a - p) ^ (b - p)), (a - p) * (b - p)));}//`化为长度为r的向量`Point trunc(double r){double l= len();if (!sgn(l))return *this;r/= l;return Point(x * r, y * r);}//`逆时针旋转90度`Point rotleft(){return Point(-y, x);}//`顺时针旋转90度`Point rotright(){return Point(y, -x);}//`绕着p点逆时针旋转angle`Point rotate(Point p, double angle){Point v= (*this) - p;double c= cos(angle), s= sin(angle);return Point(p.x + v.x * c - v.y * s, p.y + v.x * s + v.y * c);}
};
/** Stores two points* Line()                         - Empty constructor* Line(Point _s,Point _e)        - Line through _s and _e* operator ==                    - checks if two points are same* Line(Point p,double angle)     - one end p , another end at angle degree* Line(double a,double b,double c) - Line of equation ax + by + c = 0* input()                        - inputs s and e* adjust()                       - orders in such a way that s < e* length()                       - distance of se* angle()                        - return 0 <= angle < pi* relation(Point p)              - 3 if point is on line*                                  1 if point on the left of line*                                  2 if point on the right of line* pointonseg(double p)           - return true if point on segment* parallel(Line v)               - return true if they are parallel* segcrossseg(Line v)            - returns 0 if does not intersect*                                  returns 1 if non-standard intersection*                                  returns 2 if intersects* linecrossseg(Line v)           - line and seg* linecrossline(Line v)          - 0 if parallel*                                  1 if coincides*                                  2 if intersects* crosspoint(Line v)             - returns intersection point* dispointtoline(Point p)        - distance from point p to the line* dispointtoseg(Point p)         - distance from p to the segment* dissegtoseg(Line v)            - distance of two segment* lineprog(Point p)              - returns projected point p on se line* symmetrypoint(Point p)         - returns reflection point of p over se**/
struct Line
{Point s, e;Line(){}Line(Point _s, Point _e){s= _s;e= _e;}bool operator==(Line v){return (s == v.s) && (e == v.e);}//`根据一个点和倾斜角angle确定直线,0<=angle<pi`Line(Point p, double angle){s= p;if (sgn(angle - pi / 2) == 0) {e= (s + Point(0, 1));}else {e= (s + Point(1, tan(angle)));}}//ax+by+c=0Line(double a, double b, double c){if (sgn(a) == 0) {s= Point(0, -c / b);e= Point(1, -c / b);}else if (sgn(b) == 0) {s= Point(-c / a, 0);e= Point(-c / a, 1);}else {s= Point(0, -c / b);e= Point(1, (-c - a) / b);}}void input(){s.input();e.input();}void adjust(){if (e < s)swap(s, e);}//求线段长度double length(){return s.distance(e);}//`返回直线倾斜角 0<=angle<pi`double angle(){double k= atan2(e.y - s.y, e.x - s.x);if (sgn(k) < 0)k+= pi;if (sgn(k - pi) == 0)k-= pi;return k;}//`点和直线关系`//`1  在左侧`//`2  在右侧`//`3  在直线上`int relation(Point p){int c= sgn((p - s) ^ (e - s));if (c < 0)return 1;else if (c > 0)return 2;elsereturn 3;}// 点在线段上的判断bool pointonseg(Point p){return sgn((p - s) ^ (e - s)) == 0 && sgn((p - s) * (p - e)) <= 0;}//`两向量平行(对应直线平行或重合)`bool parallel(Line v){return sgn((e - s) ^ (v.e - v.s)) == 0;}//`两线段相交判断`//`2 规范相交`//`1 非规范相交`//`0 不相交`int segcrossseg(Line v){int d1= sgn((e - s) ^ (v.s - s));int d2= sgn((e - s) ^ (v.e - s));int d3= sgn((v.e - v.s) ^ (s - v.s));int d4= sgn((v.e - v.s) ^ (e - v.s));if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2)return 2;return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) || (d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) || (d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0)|| (d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);}//`直线和线段相交判断`//`-*this line   -v seg`//`2 规范相交`//`1 非规范相交`//`0 不相交`int linecrossseg(Line v){int d1= sgn((e - s) ^ (v.s - s));int d2= sgn((e - s) ^ (v.e - s));if ((d1 ^ d2) == -2)return 2;return (d1 == 0 || d2 == 0);}//`两直线关系`//`0 平行`//`1 重合`//`2 相交`int linecrossline(Line v){if ((*this).parallel(v))return v.relation(s) == 3;return 2;}//`求两直线的交点`//`要保证两直线不平行或重合`Point crosspoint(Line v){double a1= (v.e - v.s) ^ (s - v.s);double a2= (v.e - v.s) ^ (e - v.s);return Point((s.x * a2 - e.x * a1) / (a2 - a1), (s.y * a2 - e.y * a1) / (a2 - a1));}//点到直线的距离double dispointtoline(Point p){return fabs((p - s) ^ (e - s)) / length();}//点到线段的距离double dispointtoseg(Point p){if (sgn((p - s) * (e - s)) < 0 || sgn((p - e) * (s - e)) < 0)return min(p.distance(s), p.distance(e));return dispointtoline(p);}//`返回线段到线段的距离`//`前提是两线段不相交，相交距离就是0了`double dissegtoseg(Line v){return min(min(dispointtoseg(v.s), dispointtoseg(v.e)), min(v.dispointtoseg(s), v.dispointtoseg(e)));}//`返回点p在直线上的投影`Point lineprog(Point p){return s + (((e - s) * ((e - s) * (p - s))) / ((e - s).len2()));}//`返回点p关于直线的对称点`Point symmetrypoint(Point p){Point q= lineprog(p);return Point(2 * q.x - p.x, 2 * q.y - p.y);}
};
//圆
struct circle
{Point p; //圆心double r; //半径circle(){}circle(Point _p, double _r){p= _p;r= _r;}circle(double x, double y, double _r){p= Point(x, y);r= _r;}//`三角形的外接圆`//`需要Point的+ /  rotate()  以及Line的crosspoint()`//`利用两条边的中垂线得到圆心`//`测试：UVA12304`circle(Point a, Point b, Point c){Line u= Line((a + b) / 2, ((a + b) / 2) + ((b - a).rotleft()));Line v= Line((b + c) / 2, ((b + c) / 2) + ((c - b).rotleft()));p= u.crosspoint(v);r= p.distance(a);}//`三角形的内切圆`//`参数bool t没有作用，只是为了和上面外接圆函数区别`//`测试：UVA12304`circle(Point a, Point b, Point c, bool t){Line u, v;double m= atan2(b.y - a.y, b.x - a.x), n= atan2(c.y - a.y, c.x - a.x);u.s= a;u.e= u.s + Point(cos((n + m) / 2), sin((n + m) / 2));v.s= b;m= atan2(a.y - b.y, a.x - b.x), n= atan2(c.y - b.y, c.x - b.x);v.e= v.s + Point(cos((n + m) / 2), sin((n + m) / 2));p= u.crosspoint(v);r= Line(a, b).dispointtoseg(p);}//输入void input(){p.input();scanf("%lf", &r);}//输出void output(){printf("%.2lf %.2lf %.2lf\n", p.x, p.y, r);}bool operator==(circle v){return (p == v.p) && sgn(r - v.r) == 0;}bool operator<(circle v) const{return ((p < v.p) || ((p == v.p) && sgn(r - v.r) < 0));}//面积double area(){return pi * r * r;}//周长double circumference(){return 2 * pi * r;}//`点和圆的关系`//`0 圆外`//`1 圆上`//`2 圆内`int relation(Point b){double dst= b.distance(p);if (sgn(dst - r) < 0)return 2;else if (sgn(dst - r) == 0)return 1;return 0;}//`线段和圆的关系`//`比较的是圆心到线段的距离和半径的关系`int relationseg(Line v){double dst= v.dispointtoseg(p);if (sgn(dst - r) < 0)return 2;else if (sgn(dst - r) == 0)return 1;return 0;}//`直线和圆的关系`//`比较的是圆心到直线的距离和半径的关系`int relationline(Line v){double dst= v.dispointtoline(p);if (sgn(dst - r) < 0)return 2;else if (sgn(dst - r) == 0)return 1;return 0;}//`两圆的关系`//`5 相离`//`4 外切`//`3 相交`//`2 内切`//`1 内含`//`需要Point的distance`//`测试：UVA12304`int relationcircle(circle v){double d= p.distance(v.p);if (sgn(d - r - v.r) > 0)return 5;if (sgn(d - r - v.r) == 0)return 4;double l= fabs(r - v.r);if (sgn(d - r - v.r) < 0 && sgn(d - l) > 0)return 3;if (sgn(d - l) == 0)return 2;if (sgn(d - l) < 0)return 1;}//`求两个圆的交点，返回0表示没有交点，返回1是一个交点，2是两个交点`//`需要relationcircle`//`测试：UVA12304`int pointcrosscircle(circle v, Point& p1, Point& p2){int rel= relationcircle(v);if (rel == 1 || rel == 5)return 0;double d= p.distance(v.p);double l= (d * d + r * r - v.r * v.r) / (2 * d);double h= sqrt(r * r - l * l);Point tmp= p + (v.p - p).trunc(l);p1= tmp + ((v.p - p).rotleft().trunc(h));p2= tmp + ((v.p - p).rotright().trunc(h));if (rel == 2 || rel == 4)return 1;return 2;}//`求直线和圆的交点，返回交点个数`int pointcrossline(Line v, Point& p1, Point& p2){if (!(*this).relationline(v))return 0;Point a= v.lineprog(p);double d= v.dispointtoline(p);d= sqrt(r * r - d * d);if (sgn(d) == 0) {p1= a;p2= a;return 1;}p1= a + (v.e - v.s).trunc(d);p2= a - (v.e - v.s).trunc(d);return 2;}//`得到过a,b两点，半径为r1的两个圆`int gercircle(Point a, Point b, double r1, circle& c1, circle& c2){circle x(a, r1), y(b, r1);int t= x.pointcrosscircle(y, c1.p, c2.p);if (!t)return 0;c1.r= c2.r= r;return t;}//`得到与直线u相切，过点q,半径为r1的圆`//`测试：UVA12304`int getcircle(Line u, Point q, double r1, circle& c1, circle& c2){double dis= u.dispointtoline(q);if (sgn(dis - r1 * 2) > 0)return 0;if (sgn(dis) == 0) {c1.p= q + ((u.e - u.s).rotleft().trunc(r1));c2.p= q + ((u.e - u.s).rotright().trunc(r1));c1.r= c2.r= r1;return 2;}Line u1= Line((u.s + (u.e - u.s).rotleft().trunc(r1)), (u.e + (u.e - u.s).rotleft().trunc(r1)));Line u2= Line((u.s + (u.e - u.s).rotright().trunc(r1)), (u.e + (u.e - u.s).rotright().trunc(r1)));circle cc= circle(q, r1);Point p1, p2;if (!cc.pointcrossline(u1, p1, p2))cc.pointcrossline(u2, p1, p2);c1= circle(p1, r1);if (p1 == p2) {c2= c1;return 1;}c2= circle(p2, r1);return 2;}//`同时与直线u,v相切，半径为r1的圆`//`测试：UVA12304`int getcircle(Line u, Line v, double r1, circle& c1, circle& c2, circle& c3, circle& c4){if (u.parallel(v))return 0; //两直线平行Line u1= Line(u.s + (u.e - u.s).rotleft().trunc(r1), u.e + (u.e - u.s).rotleft().trunc(r1));Line u2= Line(u.s + (u.e - u.s).rotright().trunc(r1), u.e + (u.e - u.s).rotright().trunc(r1));Line v1= Line(v.s + (v.e - v.s).rotleft().trunc(r1), v.e + (v.e - v.s).rotleft().trunc(r1));Line v2= Line(v.s + (v.e - v.s).rotright().trunc(r1), v.e + (v.e - v.s).rotright().trunc(r1));c1.r= c2.r= c3.r= c4.r= r1;c1.p= u1.crosspoint(v1);c2.p= u1.crosspoint(v2);c3.p= u2.crosspoint(v1);c4.p= u2.crosspoint(v2);return 4;}//`同时与不相交圆cx,cy相切，半径为r1的圆`//`测试：UVA12304`int getcircle(circle cx, circle cy, double r1, circle& c1, circle& c2){circle x(cx.p, r1 + cx.r), y(cy.p, r1 + cy.r);int t= x.pointcrosscircle(y, c1.p, c2.p);if (!t)return 0;c1.r= c2.r= r1;return t;}//`过一点作圆的切线(先判断点和圆的关系)`//`测试：UVA12304`int tangentline(Point q, Line& u, Line& v){int x= relation(q);if (x == 2)return 0;if (x == 1) {u= Line(q, q + (q - p).rotleft());v= u;return 1;}double d= p.distance(q);double l= r * r / d;double h= sqrt(r * r - l * l);u= Line(q, p + ((q - p).trunc(l) + (q - p).rotleft().trunc(h)));v= Line(q, p + ((q - p).trunc(l) + (q - p).rotright().trunc(h)));return 2;}//`求两圆相交的面积`double areacircle(circle v){int rel= relationcircle(v);if (rel >= 4)return 0.0;if (rel <= 2)return min(area(), v.area());double d= p.distance(v.p);double hf= (r + v.r + d) / 2.0;double ss= 2 * sqrt(hf * (hf - r) * (hf - v.r) * (hf - d));double a1= acos((r * r + d * d - v.r * v.r) / (2.0 * r * d));a1= a1 * r * r;double a2= acos((v.r * v.r + d * d - r * r) / (2.0 * v.r * d));a2= a2 * v.r * v.r;return a1 + a2 - ss;}//`求圆和三角形pab的相交面积`//`测试：POJ3675 HDU3982 HDU2892`double areatriangle(Point a, Point b){if (sgn((p - a) ^ (p - b)) == 0)return 0.0;Point q[5];int len= 0;q[len++]= a;Line l(a, b);Point p1, p2;if (pointcrossline(l, q[1], q[2]) == 2) {if (sgn((a - q[1]) * (b - q[1])) < 0)q[len++]= q[1];if (sgn((a - q[2]) * (b - q[2])) < 0)q[len++]= q[2];}q[len++]= b;if (len == 4 && sgn((q[0] - q[1]) * (q[2] - q[1])) > 0)swap(q[1], q[2]);double res= 0;for (int i= 0; i < len - 1; i++) {if (relation(q[i]) == 0 || relation(q[i + 1]) == 0) {double arg= p.rad(q[i], q[i + 1]);res+= r * r * arg / 2.0;}else {res+= fabs((q[i] - p) ^ (q[i + 1] - p)) / 2.0;}}return res;}
};/** n,p  Line l for each side* input(int _n)                        - inputs _n size polygon* add(Point q)                         - adds a point at end of the list* getline()                            - populates line array* cmp                                  - comparision in convex_hull order* norm()                               - sorting in convex_hull order* getconvex(polygon &convex)           - returns convex hull in convex* Graham(polygon &convex)              - returns convex hull in convex* isconvex()                           - checks if convex* relationpoint(Point q)               - returns 3 if q is a vertex*                                                2 if on a side*                                                1 if inside*                                                0 if outside* convexcut(Line u,polygon &po)        - left side of u in po* gercircumference()                   - returns side length* getarea()                            - returns area* getdir()                             - returns 0 for cw, 1 for ccw* getbarycentre()                      - returns barycenter**/
struct polygon
{int n;Point p[maxp];Line l[maxp];void input(int _n){n= _n;for (int i= 0; i < n; i++)p[i].input();}void add(Point q){p[n++]= q;}void getline(){for (int i= 0; i < n; i++) {l[i]= Line(p[i], p[(i + 1) % n]);}}struct cmp{Point p;cmp(const Point& p0){p= p0;}bool operator()(const Point& aa, const Point& bb){Point a= aa, b= bb;int d= sgn((a - p) ^ (b - p));if (d == 0) {return sgn(a.distance(p) - b.distance(p)) < 0;}return d > 0;}};//`进行极角排序`//`首先需要找到最左下角的点`//`需要重载号好Point的 < 操作符(min函数要用) `void norm(){Point mi= p[0];for (int i= 1; i < n; i++)mi= min(mi, p[i]);sort(p, p + n, cmp(mi));}//`得到凸包`//`得到的凸包里面的点编号是0$\sim$n-1的`//`两种凸包的方法`//`注意如果有影响，要特判下所有点共点，或者共线的特殊情况`//`测试 LightOJ1203  LightOJ1239`void getconvex(polygon& convex){sort(p, p + n);convex.n= n;for (int i= 0; i < min(n, 2); i++) {convex.p[i]= p[i];}if (convex.n == 2 && (convex.p[0] == convex.p[1]))convex.n--; //特判if (n <= 2)return;int& top= convex.n;top= 1;for (int i= 2; i < n; i++) {while (top && sgn((convex.p[top] - p[i]) ^ (convex.p[top - 1] - p[i])) <= 0)top--;convex.p[++top]= p[i];}int temp= top;convex.p[++top]= p[n - 2];for (int i= n - 3; i >= 0; i--) {while (top != temp && sgn((convex.p[top] - p[i]) ^ (convex.p[top - 1] - p[i])) <= 0)top--;convex.p[++top]= p[i];}if (convex.n == 2 && (convex.p[0] == convex.p[1]))convex.n--; //特判convex.norm(); //`原来得到的是顺时针的点，排序后逆时针`}//`得到凸包的另外一种方法`//`测试 LightOJ1203  LightOJ1239`void Graham(polygon& convex){norm();int& top= convex.n;top= 0;if (n == 1) {top= 1;convex.p[0]= p[0];return;}if (n == 2) {top= 2;convex.p[0]= p[0];convex.p[1]= p[1];if (convex.p[0] == convex.p[1])top--;return;}convex.p[0]= p[0];convex.p[1]= p[1];top= 2;for (int i= 2; i < n; i++) {while (top > 1 && sgn((convex.p[top - 1] - convex.p[top - 2]) ^ (p[i] - convex.p[top - 2])) <= 0)top--;convex.p[top++]= p[i];}if (convex.n == 2 && (convex.p[0] == convex.p[1]))convex.n--; //特判}//`判断是不是凸的`bool isconvex(){bool s[2];memset(s, false, sizeof(s));for (int i= 0; i < n; i++) {int j= (i + 1) % n;int k= (j + 1) % n;s[sgn((p[j] - p[i]) ^ (p[k] - p[i])) + 1]= true;if (s[0] && s[2])return false;}return true;}//`判断点和任意多边形的关系`//` 3 点上`//` 2 边上`//` 1 内部`//` 0 外部`int relationpoint(Point q){for (int i= 0; i < n; i++) {if (p[i] == q)return 3;}getline();for (int i= 0; i < n; i++) {if (l[i].pointonseg(q))return 2;}int cnt= 0;for (int i= 0; i < n; i++) {int j= (i + 1) % n;int k= sgn((q - p[j]) ^ (p[i] - p[j]));int u= sgn(p[i].y - q.y);int v= sgn(p[j].y - q.y);if (k > 0 && u < 0 && v >= 0)cnt++;if (k < 0 && v < 0 && u >= 0)cnt--;}return cnt != 0;}//`直线u切割凸多边形左侧`//`注意直线方向`//`测试：HDU3982`void convexcut(Line u, polygon& po){int& top= po.n; //注意引用top= 0;for (int i= 0; i < n; i++) {int d1= sgn((u.e - u.s) ^ (p[i] - u.s));int d2= sgn((u.e - u.s) ^ (p[(i + 1) % n] - u.s));if (d1 >= 0)po.p[top++]= p[i];if (d1 * d2 < 0)po.p[top++]= u.crosspoint(Line(p[i], p[(i + 1) % n]));}}//`得到周长`//`测试 LightOJ1239`double getcircumference(){double sum= 0;for (int i= 0; i < n; i++) {sum+= p[i].distance(p[(i + 1) % n]);}return sum;}//`得到面积`double getarea(){double sum= 0;for (int i= 0; i < n; i++) {sum+= (p[i] ^ p[(i + 1) % n]);}return fabs(sum) / 2;}//`得到方向`//` 1 表示逆时针，0表示顺时针`bool getdir(){double sum= 0;for (int i= 0; i < n; i++)sum+= (p[i] ^ p[(i + 1) % n]);if (sgn(sum) > 0)return 1;return 0;}//`得到重心`Point getbarycentre(){Point ret(0, 0);double area= 0;for (int i= 1; i < n - 1; i++) {double tmp= (p[i] - p[0]) ^ (p[i + 1] - p[0]);if (sgn(tmp) == 0)continue;area+= tmp;ret.x+= (p[0].x + p[i].x + p[i + 1].x) / 3 * tmp;ret.y+= (p[0].y + p[i].y + p[i + 1].y) / 3 * tmp;}if (sgn(area))ret= ret / area;return ret;}//`多边形和圆交的面积`//`测试：POJ3675 HDU3982 HDU2892`double areacircle(circle c){double ans= 0;for (int i= 0; i < n; i++) {int j= (i + 1) % n;if (sgn((p[j] - c.p) ^ (p[i] - c.p)) >= 0)ans+= c.areatriangle(p[i], p[j]);elseans-= c.areatriangle(p[i], p[j]);}return fabs(ans);}//`多边形和圆关系`//` 2 圆完全在多边形内`//` 1 圆在多边形里面，碰到了多边形边界`//` 0 其它`int relationcircle(circle c){getline();int x= 2;if (relationpoint(c.p) != 1)return 0; //圆心不在内部for (int i= 0; i < n; i++) {if (c.relationseg(l[i]) == 2)return 0;if (c.relationseg(l[i]) == 1)x= 1;}return x;}
};
//`AB X AC`
double cross(Point A, Point B, Point C)
{return (B - A) ^ (C - A);
}int main()
{//rd_test();int t;read(t);while (t--) {double r1, x1, y1;double r2, x2, y2;double a;scanf("%lf%lf%lf", &r1, &x1, &y1);scanf("%lf%lf%lf", &r2, &x2, &y2);scanf("%lf", &a);double newr1, newr2;newr1= sqrt(r1 * r1 - a * a / 4) - a / 2;newr2= sqrt(r2 * r2 - a * a / 4) - a / 2;circle A(x1, y1, newr1);circle B(x2, y2, newr2);double sum1= A.areacircle(B);double sum2= A.area();printf("%.6lf\n", sum1 / sum2);}//Time_test();
}