P4159 [SCOI2009] 迷路

题意：

该有向图有 n 个节点，节点从 1 至 nn 编号，windy 从节点 1 出发，他必须恰好在 t 时刻到达节点 n。

现在给出该有向图(带边权)，你能告诉 windy 总共有多少种不同的路径吗？

答案对 2009 取模。

题解：

如果边权只有0和1，那么就是矩阵快速幂的板子题，可惜不是，现在边权大于1，就不是存板子，但是边权也小于10，那也就是我们可以把这个1个点拆开看，最多也就拆成9个而已。
我们令序数对(i，j)，i属于[1,n],j∈[0,8],表示点i拆成的第j个点，其中第0个点是真点，其余是假点
我们令(i,j)(j属于[1,8])表示到真点(i,0)的距离为j的假点，只要让(i,j)向(i,j-1)连一条边权为1的边
而对于原图中一条从u到v的边权为w的边，我们只要让(u,0)向(v,w-1)连一条边权为1的边
有点像分层图的感觉，就是把边权给分解开了

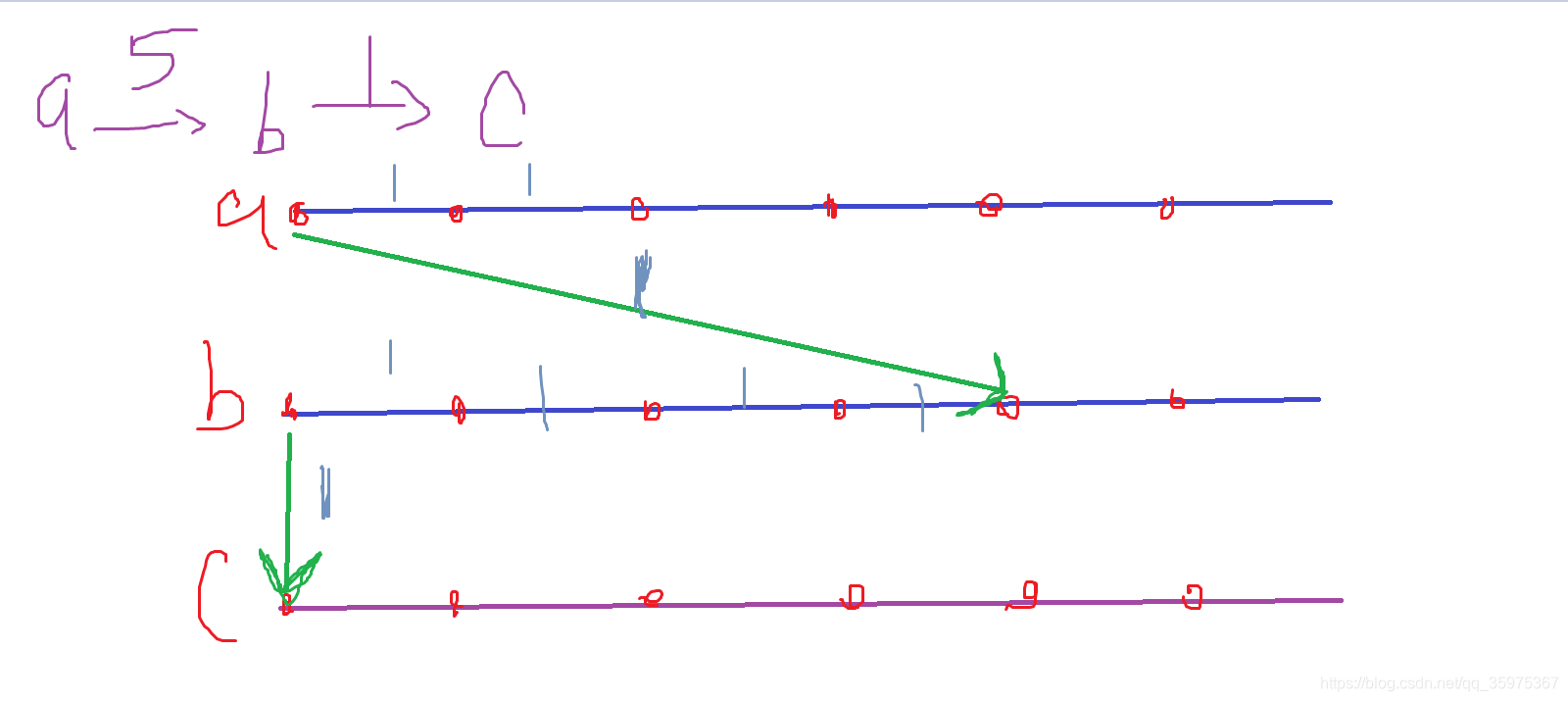
这样就还原了一开始那种只有01的边，此时矩阵变成9n * 9n的矩阵，直接跑矩阵快速幂就行

代码：