.net core webapi 前后端开发分离后的配置和部署

背景：现在越来越多的企业都采用了在开发上前后端分离，前后端开发上的分离有很多种，那么今天，我来分享一下项目中得的前后端分离。

B/S Saas 项目：（这个项目可以理解成个人中心，当然不止这么点功能）

前端：node.js + vue

后端：.net core webapi

前端安装 node.js 跟创建vue项目这些不是这篇文章的重点，重点在于项目完成后的部署。

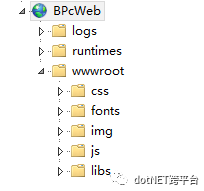
.net core webapi创建后，默认就创建了一个wwwroot的文件夹，这个文件夹是用来放置静态文件的，所以，我们可以理解成，这个文件夹将放置我们的build好的前端项目。

640?wx_fmt=png

OK，到现在来讲，有一个很有意思的发现（也可以是一点意思都没有，因为都是同一个爸生的），这项目的部署跟mvc的部署的很像（这里不涉及底层运行，只是一个发布后简单的像而已）。

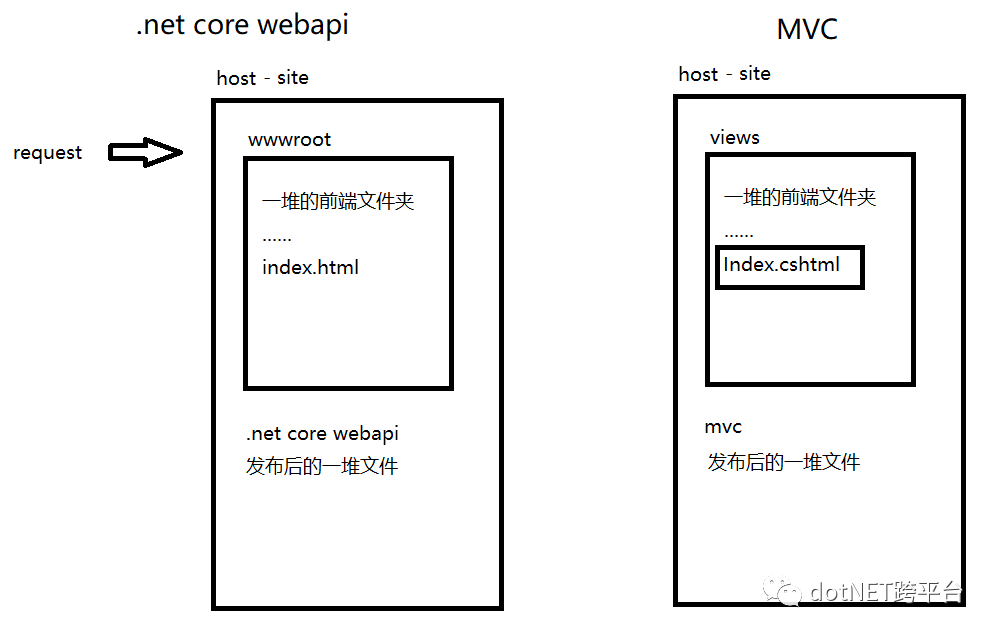
640?wx_fmt=png

由上图就足够清晰了，这样的部署是属于开发上的前后端分离，他们同属于一个站点，绑定同一个域名，所以不涉及跨域，外部不能直接调用webapi（安全上还是有保证D）。

那么这样的部署却很简单，仅仅是在 Startup 里面的 Configure 设置一下即可

            //设置主页
            app.UseDefaultFiles();

//这个是.net core webapi 访问wwwroot文件夹的配置，开启静态文件
            app.UseStaticFiles();

            app.UseMvc(routes =>
            {
                routes.MapRoute(
                    name: "default",
                    template: "api/{controller=Login}/{action=Get}/{id?}");
            });

1、首先是设置主页

这里直接使用的是默认的，就是 UseDefaultFiles 会重定向到 default.htm、default.html、index.htm、index.html。当然你也可以指定设置的首页（指定的页面是可以自定义的！）

            //设置主页
            DefaultFilesOptions defaultFilesOptions = new DefaultFilesOptions();
            defaultFilesOptions.DefaultFileNames.Clear();
            defaultFilesOptions.DefaultFileNames.Add("index.html");

            app.UseDefaultFiles(defaultFilesOptions);

这样就设定了重定向到 index.html，那为什么前面用了 Clear，其实个人认为仅仅是为了保险，因为

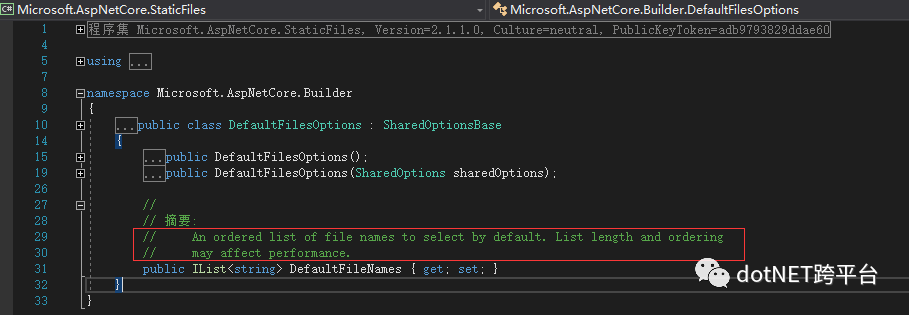
640?wx_fmt=png

2、开启静态文件，UseDefaultFiles 仅仅是一个重定向URL而不是真的提供一个文件，真正提供静态文件的还是 UseStaticFiles。这就是为什么要优先设置 UseDefaultFiles 再到 UseStaticFiles的原因。当然，提供静态文件也提供了多个重载，可以提供一个相对路径，还有静态文件目录的选择。

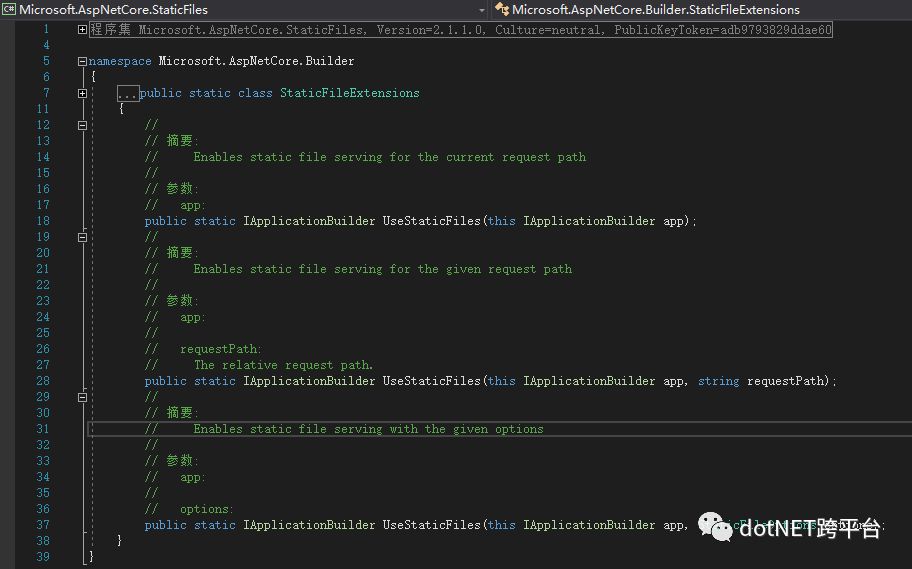
640?wx_fmt=png

            //这个是.net core webapi 访问wwwroot文件夹的配置，开启静态文件
            StaticFileOptions staticFileOptions = new StaticFileOptions();
            staticFileOptions.FileProvider = new Microsoft.Extensions.FileProviders.PhysicalFileProvider(@"D:\testsite\wwwroot\");//指定目录你站点api的要访问的wwwroot目录   

            app.UseStaticFiles(staticFileOptions);

上面这种写法也同样可以，当然指定的目录也同样可以放到配置文件里面去，但是这种做法一般都放在类似FTP的项目上。因为如果是指定的目录脱离了 webapi 项目 wwwroot ，甚至是 wwwroot 下的文件夹都不可以访问到静态页面的。

3、使用MVC并配置路由，开启了静态文件的访问之后，就交由mvc来处理了，这个是webapi项目，所以配置api的路由就可以了。（除了上面的1、2顺序不可以改变之外，mvc中配置的路由所放置的顺序倒没影响，因为这不是一个mvc项目）

好了，前后端都开发好之后，部署到服务器，仅是上面在Startup的配置即可。.net core 还是非常非常方便的。

640?wx_fmt=png