P2163 [SHOI2007]园丁的烦恼

题意：

在一个二维平面内有一些点，给你一个左上角和右下角的点，问这个范围内有多少点

题解：

二维数点模板题
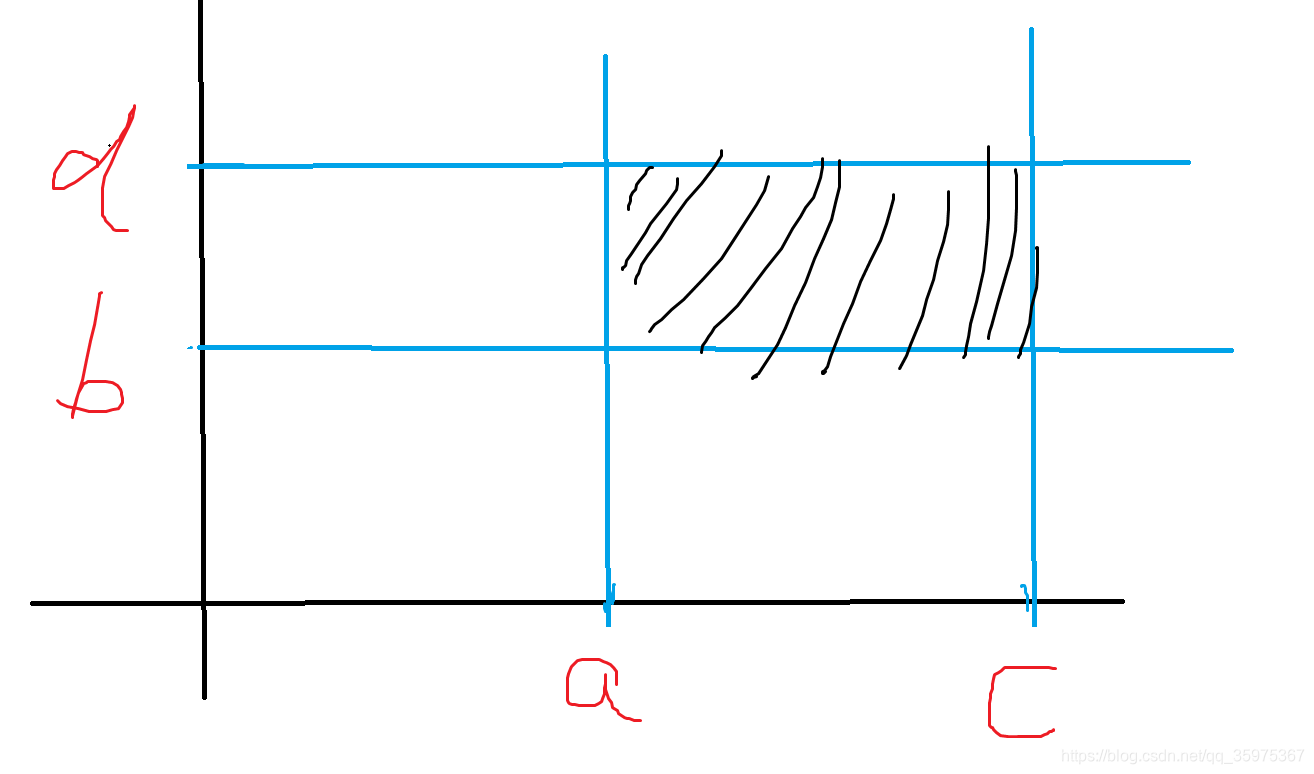
我们设F(a,b)表示以(0,0)为左下角，(a,b)为右上角的矩阵内有多少点
如图不难得到：
黑色部分为=F(c,d)+F(a-1,b-1)-F(a-1,d)-F(c,b-1)
(不就是二维前缀和)

因为数据范围过大，所以横纵坐标都离散化处理。
现在我们如何求(0,0)到(x,y)内点的数量
我们把矩阵内的点看作是插入操作，相当于在矩阵中(x,y)位置+1.
把所有插入操作和查询操作以x坐标为第一关键字，y坐标为第二关键字排序
若第i个是查询操作，仅有[1,i-1]中的插入操作能影响它，因为第i个操作后面的操作坐标都比它大
同样第i个操作是插入操作，不会影响到前面的查询
这样就利用树状数组实现二维数点问题
CDQ也可以二维数点，也是模板题

主席树也可以二维数点，这里有详细讲解

代码：

树状数组代码：

#include<stdio.h>
#include<cstring>
#include<algorithm>
#include<math.h>
#include<vector>
#define re register int
#define rl register ll
#define lowbit(x) x&(-x)
using namespace std;
typedef long long ll;
int read() {re x=0,f=1;char ch=getchar();while(ch<'0' || ch>'9') {if(ch=='-')	f=-1;ch=getchar();}while(ch>='0' && ch<='9') {x=10*x+ch-'0';ch=getchar();}return x*f;
}
inline void write(int x) {if(x>9)	write(x/10);putchar(x%10+'0');
}
inline char GetChar() {char ch=getchar();while(ch!='A' && ch!='B' && ch!='C')	ch=getchar();return ch;
}const int Size=500005;
int n,m,tot,maxn,ny[Size*5];
struct zyd {int id,x,y,k,dt;
} Q[Size*5];
inline void Push(int x,int y,int k,int id) {Q[++tot].x=x;Q[tot].y=y;Q[tot].k=k;Q[tot].id=id;Q[tot].dt=tot;
}
inline bool comp(zyd jzm,zyd xjp) {if(jzm.x!=xjp.x)	return jzm.x<xjp.x;if(jzm.y!=xjp.y)	return jzm.y<xjp.y;return jzm.dt<xjp.dt;
}
int tree[Size];
inline void update(int x) {for(re i=x; i<=maxn; i+=lowbit(i)) {tree[i]++;}
}
inline int query(int x) {int ans=0;for(re i=x; i; i-=lowbit(i)) {ans+=tree[i];}return ans;
}
int out[Size];
void solve() {n=read();m=read();for(re i=1; i<=n; i++) {int x=read();int y=read();Push(x,y,0,0);}for(re i=1; i<=m; i++) {int a=read();int b=read();int c=read();int d=read();Push(c,d,1,i);Push(a-1,b-1,1,i);Push(a-1,d,-1,i);Push(c,b-1,-1,i);}sort(Q+1,Q+1+tot,comp);for(re i=1; i<=tot; i++) {ny[i]=Q[i].y;}sort(ny+1,ny+1+tot);maxn=unique(ny+1,ny+1+tot)-(ny+1);for(re i=1; i<=tot; i++) {Q[i].y=lower_bound(ny+1,ny+1+maxn,Q[i].y)-ny;}for(re i=1; i<=tot; i++) {if(!Q[i].k) {update(Q[i].y);} else if(Q[i].k==1) {out[Q[i].id]+=query(Q[i].y);} else {out[Q[i].id]-=query(Q[i].y);}}for(re i=1; i<=m; i++) {printf("%d\n",out[i]);}
}int main() {solve();return 0;
}

CDQ代码:

#include<bits/stdc++.h>
#define maxn 5000005 * 5
using namespace std;
inline int read()
{char x = getchar();int lin = 0, f = 1;while(x < '0' || x > '9'){if(x == '-') f = -1;x = getchar();}while(x >= '0' && x <= '9'){lin = lin * 10 + x - '0';x = getchar();}return lin * f;
}
struct st{int x,y,typ,add,id,ans;
}s[maxn],ce[maxn];
int n,m,x,y,tot,a,b,c,d,ans[maxn];
void add(int x,int y,int typ,int add,int id,int ans)
{s[++tot] = (st) {x,y,typ,add,id,ans};
}
bool com(st a,st b)
{if(a.x == b.x)if(a.y == b.y)return a.typ < b.typ;else return a.y < b.y;return a.x < b.x;
}
void cdq(int l,int r)
{if(l == r) return;int mid = l + r >> 1;cdq(l,mid);cdq(mid + 1,r);int le = l,re = mid + 1,pos = 0,ans = 0;while(le <= mid || re <= r){if(re > r || (le <= mid && s[le].y <= s[re].y)){if(s[le].typ == 1) ++ans;ce[++pos] = s[le++];}else{if(s[re].typ == 2) s[re].ans += ans;ce[++pos] = s[re++];}}for(int i = 1; i <= pos; i++)s[l + i - 1] = ce[i];
}int main(){n = read(); m = read();for(int i = 1; i <= n; i++){x = read(); y = read();add(x,y,1,0,0,0);}for(int i = 1; i <= m; i++){a = read(); b = read();c = read(); d = read();add(a - 1,b - 1,2,1,i,0);add(c,d,2,1,i,0);add(a - 1,d,2,-1,i,0);add(c,b - 1,2,-1,i,0);}sort(s + 1,s + 1 + tot,com);cdq(1,tot);for(int i = 1; i <= tot; i++)if(s[i].typ == 2)ans[s[i].id] += s[i].add * s[i].ans;for(int i = 1; i <= m; i++)printf("%d\n",ans[i]);
}