很开心今天能与大家一起聊聊C# 8.0中的新特性-Async Streams,一般人通常看到这个词表情是这样.

简单说,其实就是C# 8.0中支持await foreach.

或者说,C# 8.0中支持异步返回枚举类型async Task<IEnumerable<T>>.

好吧,还不懂?Good,这篇文章就是为你写的,看完这篇文章,你就能明白它的神奇之处了.

为什么写这篇文章

Async Streams这个功能已经发布很久了,在去年的Build 2018 The future of C#就有演示,最近VS 2019发布,在该版本的Release Notes中,我再次看到了这个新特性,因为对异步编程不太熟悉,所以借着这个机会,学习新特性的同时,把异步编程重温一遍.
本文内容,参考了Bassam Alugili在InfoQ中发表的Async Streams in C# 8,撰写本博客前我已联系上该作者并得到他支持.

Async / Await

C# 5 引入了 Async/Await，用以提高用户界面响应能力和对 Web 资源的访问能力。换句话说，异步方法用于执行不阻塞线程并返回一个标量结果的异步操作。

微软多次尝试简化异步操作，因为 Async/Await 模式易于理解，所以在开发人员当中获得了良好的认可。

详见The Task asynchronous programming model in C#

常规示例

要了解问什么需要Async Streams,我们先来看看这样的一个示例,求出5以内的整数的和.

Copy

static int SumFromOneToCount(int count)
{
ConsoleExt.WriteLine("SumFromOneToCount called!");

var sum = 0;
for (var i = 0; i <= count; i++)
{
sum = sum + i;
}
return sum;
}

调用方法.

Copy

static void Main(string[] args)
{
const int count = 5;
ConsoleExt.WriteLine($"Starting the application with count: {count}!");
ConsoleExt.WriteLine("Classic sum starting.");
ConsoleExt.WriteLine($"Classic sum result: {SumFromOneToCount(count)}");
ConsoleExt.WriteLine("Classic sum completed.");
ConsoleExt.WriteLine("################################################");
}

输出结果.

可以看到,整个过程就一个线程Id为1的线程自上而下执行,这是最基础的做法.

Yield Return

接下来,我们使用yield运算符使得这个方法编程延迟加载,如下所示.

Copy

static IEnumerable<int> SumFromOneToCountYield(int count)
{
ConsoleExt.WriteLine("SumFromOneToCountYield called!");

var sum = 0;
for (var i = 0; i <= count; i++)
{
sum = sum + i;

yield return sum;
}
}

主函数

Copy

static void Main(string[] args)
{
const int count = 5;
ConsoleExt.WriteLine("Sum with yield starting.");
foreach (var i in SumFromOneToCountYield(count))
{
ConsoleExt.WriteLine($"Yield sum: {i}");
}
ConsoleExt.WriteLine("Sum with yield completed.");

ConsoleExt.WriteLine("################################################");
ConsoleExt.WriteLine(Environment.NewLine);
}

运行结果如下.

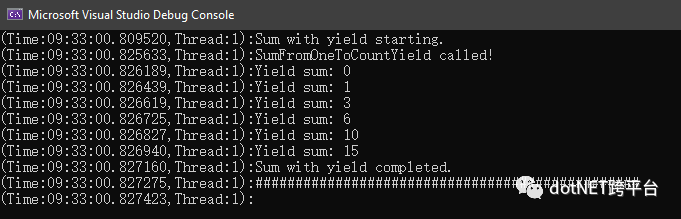
正如你在输出窗口中看到的那样，结果被分成几个部分返回，而不是作为一个值返回。以上显示的累积结果被称为惰性枚举。但是，仍然存在一个问题，即 sum 方法阻塞了代码的执行。如果你查看线程ID，可以看到所有东西都在主线程1中运行,这显然不完美,继续改造.

Async Return

我们试着将async用于SumFromOneToCount方法(没有yield关键字).

Copy

static async Task<int> SumFromOneToCountAsync(int count)
{
ConsoleExt.WriteLine("SumFromOneToCountAsync called!");

var result = await Task.Run(() =>
{
var sum = 0;

for (var i = 0; i <= count; i++)
{
sum = sum + i;
}
return sum;
});

return result;
}

主函数.

Copy

static async Task Main(string[] args)
{
const int count = 5;
ConsoleExt.WriteLine("async example starting.");

var result = await SumFromOneToCountAsync(count);
ConsoleExt.WriteLine("async Result: " + result);
ConsoleExt.WriteLine("async completed.");

ConsoleExt.WriteLine("################################################");
ConsoleExt.WriteLine(Environment.NewLine);
}

运行结果.

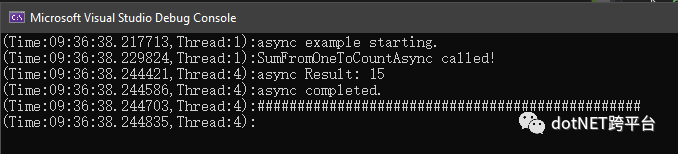
我们可以看到计算过程是在另一个线程中运行，但结果仍然是作为一个值返回！任然不完美.

如果我们想把惰性枚举（yield return）与异步方法结合起来,即返回Task<IEnumerable,这怎么实现呢?

Task<IEnumerable>

我们根据假设把代码改造一遍,使用Task<IEnumerable<T>>来进行计算.

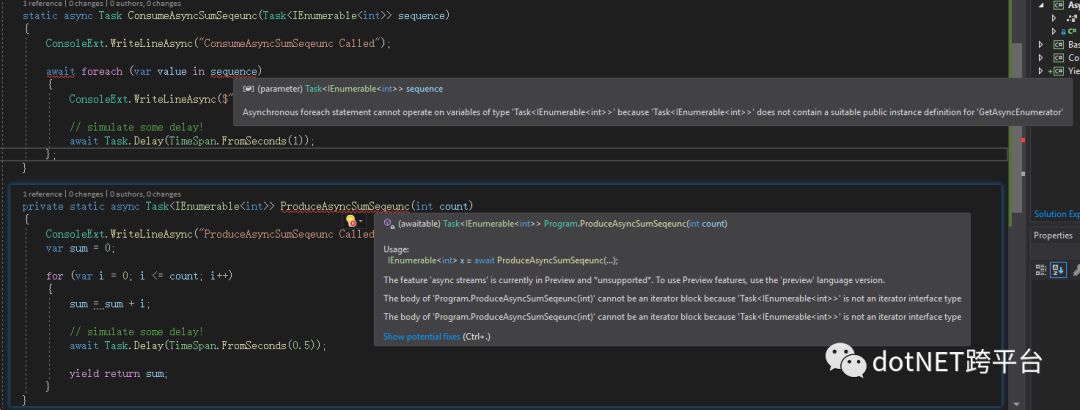
可以看到,直接出现错误.

IAsyncEnumerable

其实,在C# 8.0中Task<IEnumerable>这种组合称为IAsyncEnumerable。这个新功能为我们提供了一种很好的技术来解决拉异步延迟加载的问题，例如从网站下载数据或从文件或数据库中读取记录,与 IEnumerable 和 IEnumerator 类似，Async Streams 提供了两个新接口 IAsyncEnumerable 和 IAsyncEnumerator，定义如下：

Copy

public interface IAsyncEnumerable<out T>
{
IAsyncEnumerator<T> GetAsyncEnumerator();
}

public interface IAsyncEnumerator<out T> : IAsyncDisposable
{
Task<bool> MoveNextAsync();
T Current { get; }
}


public interface IAsyncDisposable
{
Task DiskposeAsync();
}

AsyncStream

下面,我们就来见识一下AsyncStrema的威力,我们使用IAsyncEnumerable来对函数进行改造,如下.

Copy

static async Task ConsumeAsyncSumSeqeunc(IAsyncEnumerable<int> sequence)
{
ConsoleExt.WriteLineAsync("ConsumeAsyncSumSeqeunc Called");

await foreach (var value in sequence)
{
ConsoleExt.WriteLineAsync($"Consuming the value: {value}");


await Task.Delay(TimeSpan.FromSeconds(1));
};
}

private static async IAsyncEnumerable<int> ProduceAsyncSumSeqeunc(int count)
{
ConsoleExt.WriteLineAsync("ProduceAsyncSumSeqeunc Called");
var sum = 0;

for (var i = 0; i <= count; i++)
{
sum = sum + i;


await Task.Delay(TimeSpan.FromSeconds(0.5));

yield return sum;
}
}

主函数.

Copy

static async Task Main(string[] args)
{
const int count = 5;
ConsoleExt.WriteLine("Starting Async Streams Demo!");


IAsyncEnumerable<int> pullBasedAsyncSequence = ProduceAsyncSumSeqeunc(count);


var consumingTask = Task.Run(() => ConsumeAsyncSumSeqeunc(pullBasedAsyncSequence));

await Task.Delay(TimeSpan.FromSeconds(3));

ConsoleExt.WriteLineAsync("X#X#X#X#X#X#X#X#X#X# Doing some other work X#X#X#X#X#X#X#X#X#X#");


await consumingTask;

ConsoleExt.WriteLineAsync("Async Streams Demo Done!");
}

如果一切顺利,那么就能看到这样的运行结果了.

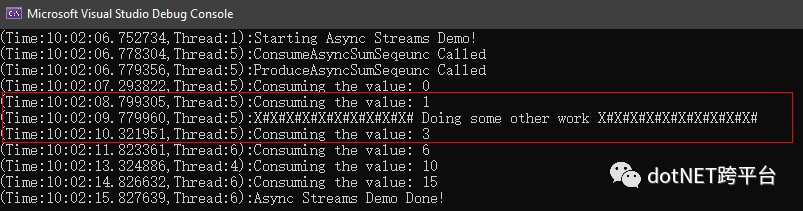
最后,看到这就是我们想要的结果,在枚举的基础上,进行了异步迭代.
可以看到,整个计算过程并没有造成主线程的阻塞,其中,值得重点关注的是红色方框区域的线程5!线程5!线程5!线程5在请求下一个结果后,并没有等待结果返回,而是去了Main()函数中做了别的事情,等待请求的结果返回后,线程5又接着执行foreach中任务.

Client/Server的异步拉取

如果还没有理解Async Streams的好处,那么我借助客户端 / 服务器端架构是演示这一功能优势的绝佳方法。

同步调用

客户端向服务器端发送请求，客户端必须等待（客户端被阻塞），直到服务器端做出响应.

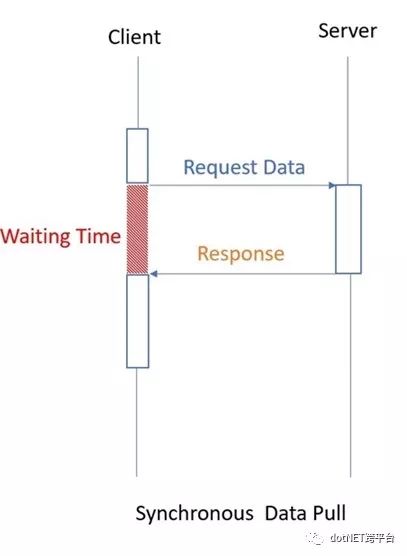
示例中Yield Return就是以这种方式执行的,所以整个过程只有一个线程即线程1在处理.

异步调用

客户端发出数据块请求，然后继续执行其他操作。一旦数据块到达，客户端就处理接收到的数据块并询问下一个数据块，依此类推，直到达到最后一个数据块为止。这正是 Async Streams 想法的来源。

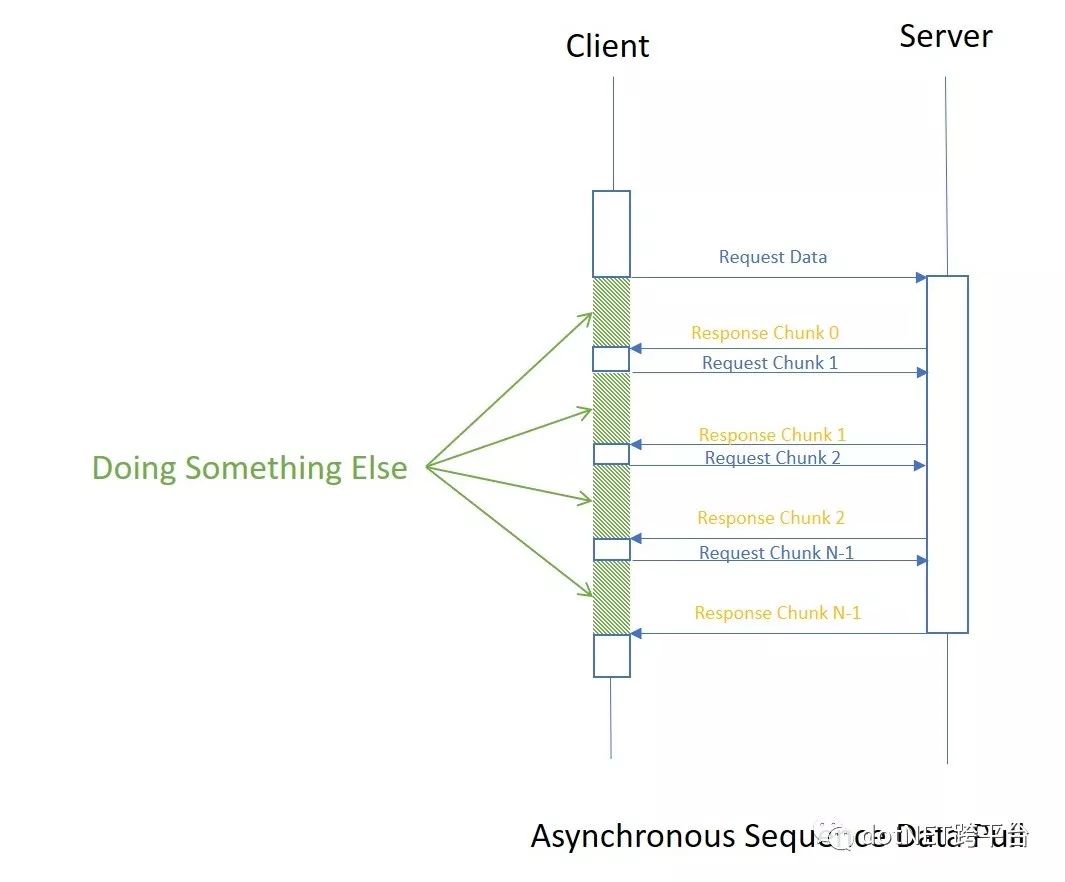
最后一个示例就是以这种方式执行的,线程5询问下一个数据后并没有等待结果返回,而是去做了Main()函数中的别的事情,数据到达后,线程5又继续处理foreach中的任务.

Tips

如果你使用的是.net core 2.2及以下版本,会遇到这样的报错.

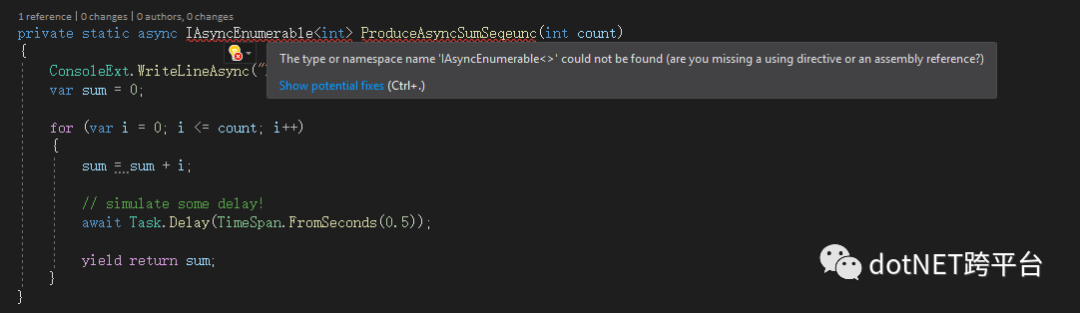
需要安装.net core 3.0 preview的SDK(截至至博客撰写日期4月9日,.net core SDK最新版本为3.0.100-preview3-010431),安装好SDK后,如果你是VS 2019正式版,可能无法选择3.0的与预览版,听过只有VS 2019 Preview才支持.Net core 3.0的预览版.

总结

我们已经讨论过 Async Streams，它是一种出色的异步拉取技术，可用于进行生成多个值的异步计算。

Async Streams 背后的编程概念是异步拉取模型。我们请求获取序列的下一个元素，并最终得到答复。Async Streams 提供了一种处理异步数据源的绝佳方法，希望对大家能够有所帮助。

文章中涉及的所有代码已保存在我的GitHub中,请尽情享用!
https://github.com/liuzhenyulive/AsyncStreamsInCShaper8.0

致谢

之前一直感觉国外的大师级开发者遥不可及甚至高高在上,在遇到Bassam Alugili之后,我才真正感受到技术交流没有高低贵贱,正如他对我说的 The most important thing in this world is sharing the knowledge!
Thank you,I will keep going!!

参考文献: Async Streams in C# 8 https://www.infoq.com/articles/Async-Streams

原文地址: https://www.cnblogs.com/CoderAyu/p/10680805.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com