原文地址：https://medium.com/scisharp/slicing-in-numsharp-e56c46826630

 

翻译初稿（英文水平有限，请多包涵）：

由于Numsharp新推出了数组切片这个牛逼的功能，所以.NET社区距离拥有强大的开源机器学习平台又近了一步。  

  

Python之所以是机器学习的首选语言，部分原因就是因为它拥有一些牛逼的库，例如NumPy和Tensorflow。与此同时，C#开发人员也迫切需要用于机器学习和数据科学的强大开源库。而NumSharp，这个由 SciSharp STACK这个开源组织全力推动的，要把NumPy移植到C#的这个项目，由于其最近全面实现了切片技术，从而向该目标迈进了一大步。该技术允许对n维数组随意的创建子集，并将其作为对原始数据的高效视图。因为这些，使得它与TensorFlow.net一起成为了C#中机器学习的有用工具。  

  

牛逼在哪？  

如果你没用过NumPy，你可能不知道切片技术有多好用， Python数组允许通过对一定范围对元素进行索引来返回数组的一个切片，其索引操作是这样的：a[start:end:step]。但是，只有使用NumPy复杂巧妙的数组实现，切片才成为一种真正强大的数据操作技术，若没有这种技术，机器学习或数据科学就无法想象了。  

  

 

 

 

而使用NumSharp写出的C#代码也是差不多一样的。但请注意，这里有一个细微的差别是，这里的切片使用的是字符串作为索引器的参数进行的索引。 

  

正如您所看到的，NumSharp团队花了很多的精力来保证代码尽可能的与Python相似。 这非常重要，因为这样的话，现有的依赖于NumPy的代码就可以很轻松的移植到C#上去了。 

 

用例: 使用同一数据的多个视图 

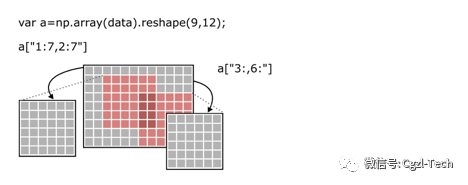
对于运行时性能，尤其是对于大规模的数据集而言，能够在不进行复制的情况下仅对函数传入和传出底层数据的本地部分（即大镜像像的一小块）是至关重要的。切片使用局部坐标进行索引的，因此您的算法无需了解数据的全局结构，这样就有效地简化了您的工作，并确保尽可能高的性能，因为避免了不必要的复制。 

 

用例：稀疏视图和递归切片 

 

除了对切片的范围指定start和end之外，再通过指定它的step（步幅），就可以创建数组的稀疏视图了。这是一个连C# 8.0新的数组切片语法都做不到的事情（据我所知）。在使用交错数据时，此功能变得非常重要。您可以通过设计算法来让它们处理连的续数据并为它们提供模拟连续数据源的稀疏切片，从而尽可能降低算法的复杂性。 

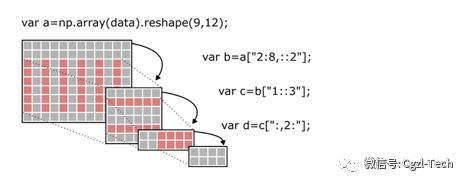
切片可以进一步切片，如果您使用高维数据的话，这也将是一个非常重要的功能。同时这也有助于减少算法的复杂性，因为通过递归切片减少了数据的维数。 

 

用例：高效地处理高维数据 

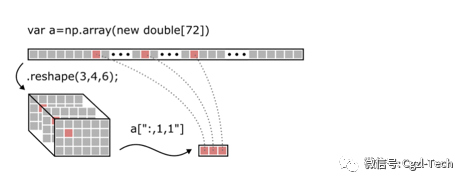
如果您需要将数据数组视为一个卷，并在不需要进行令人烦躁的坐标转换计算的情况下使用其中的某些部分，那么.reshape()方法就是您的朋友。 

所有由.reshape()或切片操作创建的数组都只是原始数据的视图。当您对视图的元素进行迭代、读取或写入时，其实您访问的是原始的数据数组。很显然，NumSharp为您做了相应的索引变换，所以您可以使用相对的坐标对切片进行索引。 

 

用例：在无任何额外成本的情况下颠倒元素的顺序 

使用值为负数的step（步幅）可以高效的反转切片的顺序。它的优点是不需要复制或列举数据就可以完成此操作，就像IEnumerable.Reverse() 一样。区别在于，视图（就是指a["::-1"]的操作结果）以相反的顺序显示数据，此外您无需对其进行列举就可以索引到该反转序列。 

 

用例：通过减少维度来降低复杂性 

当处理高维数据时，该数据的算法也会变得非常复杂。在处理NumSharp的NDArray的.ToString() 方法时（这个方法可以打印出任意高维卷）我注意到该算法通过系统地和递归地将(N-1)D卷切出ND-卷等诸如此类的方式简单而优雅的取得了结果。 

通过在可返回低维子卷的范围符号上使用NumSharp的索引符号进行切片，才使这种分而治之的方法变得可行。 

  

范围符号 vs 索引符号 

范围符号[“start:stop:step”]允许您访问具有相同维度给定卷的子范围。所以即使只划出二维矩阵的一列，仍然可以得到只有一列的二维矩阵。下面这一小段C#代码就展示了这一点： 

索引符号为您提供了一个在N维父卷指定位置切出来的(N-1)维切片。因此，用索引符号从二维矩阵中分割出一个列，可以得到一个一维向量： 

如果您一眼也没有发现差异，那么下面这两个切片定义， ange [":,2:3"] vs index [":,2"]，它们的结果是大不相同的。NumSharp wiki提供了新切片表示法的完整参考。 

 

附注：ArraySlice <T> 

在实现N维视图的切片时，我得出这样一个结论，对于.NET中的许多其他领域来说它可能很有趣，因此我将它分解出一个自己的独立库SliceAndDice。它里面有个东西叫做ArraySlice <T>，它是对所有索引的C＃数据结构（如T[]或IList<T>）的一个轻量级包装，此外它还允许您使用相同的塑形，切片和视图机制，并且无需进行任何其他的重度数值计算。它只使用了几百行代码就漂亮简洁的完成了切片的壮举。 

  

综上

NumSharp最近被赋予了同切片和视图机制，同样就是这些机制让NumPy成为Python机器学习生态最重要的库之一。SciSharp Stack作为一个开源组织，目前只有少数技术娴熟的开发人员，但他们却非常努力地要为.NET世界带来同样的魔力。NumSharp最近的这次改进就是实现这一目标的重要基石。  

---