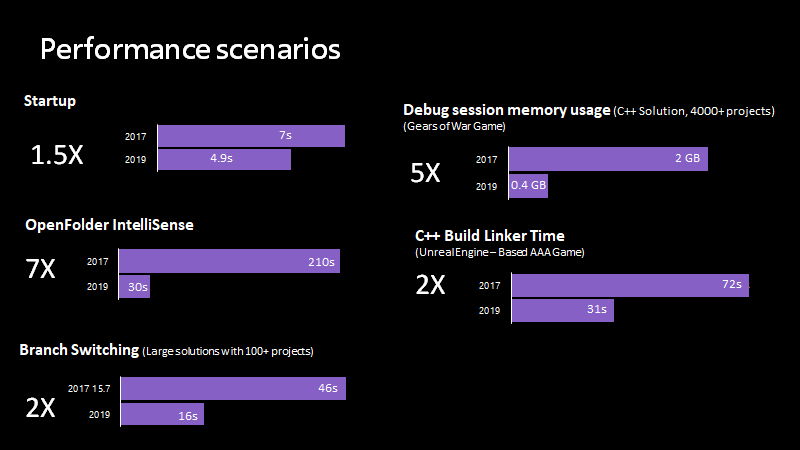
Visual Studio 2019 16.1 已正式发布，可以看到，新版本的启动速度有了显著的提升，还节省了不少的内存空间。

主要更新如下：

IDE

• 现已公开发布 Visual Studio IntelliCode，并且可以随任何支持 C#、C++、TypeScipt/JavaScript 或 XAML 的任意工作负载一起安装

• 添加了对 Per-Monitor Awareness 的支持

• 新的 codefixes 可用于 C#

• 最近使用已添加到 Visual Studio 搜索

调试器

• 改进 Source Link 身份验证

• 将 nuget.org 符号服务器添加到默认符号服务器列表中

• Time Travel Debugging 预览版现在包括异常单步执行支持

扩展性

• 在 VSIX 项目中删除了对 .resx 文件的需求（BuildTools 更新）

• VSIX 项目模板现在使用新的 SDK 版本

性能

• 性能优化，缩短解决方案加载时间

• 模板作者可以向其模板添加自定义标签

• 现在 CodeLens 支持自定义 UI

• 更新了语言服务器协议

• 优化了在解决方案、文件夹和其他视图之间的切换行为

C++

• 添加了 CMake 的编辑器内文档

• 无需额外配置或 SSH 连接，即可在 Visual Studio 中以原生方式将本地适用于 Linux 的 Windows 子系统 (WSL) 安装与 C++ 结合使用

• AddressSanitizer 现已集成到 Visual Studio，以用于 Linux 项目和 WSL

• 改进并修改了 C++ Quick Info 工具提示中的着色

• 实现了新的 C++ 代码分析快速修复

F#

• 为 F# 和 F# 工具发布了更多性能改进和大量错误修复

.NET

• 新的 .NET 生产力功能包括项目和解决方案上的一键式代码清理、新的切换块注释键盘快捷键、重构以将类型移动到其他命名空间等

• 现在可以通过开始窗口中的克隆屏幕从 SSH URI 克隆代码

• 此版本中的 .NET 生产力新增功能包括无插入类型的 intellisense 完成、切换单行注释/取消注释、将命名样式导出到 editorconfig，以及用于优先使用 namspace 内部/外部的新代码样式设置

• .NET SDK 工具新增功能，主要包括支持 .NET Core 3.0 的 WinForms 和 WPF 项目，以及 Bug 修复和性能改进

• Visual Studio SDK v16.0 已发布到 NuGet

• 适用于 .NET Core 3.0 WPF 开发的 XAML 设计器预览版已可用

Xamarin

• Xamarin 的默认 Android 体验现在支持 API 28

• Xamarin.Forms XAML 建议设计时间属性