点击上方蓝字关注“汪宇杰博客”

原文：Lee Coward

翻译：Edi Wang

导语

Visual Studio 2019 16.3 和 .NET Core 3.0 Preview 7 改进了 Windows 上 .NET Core 的安装体验。目标是减少计算机上可能存在的 .NET  Core 版本的数量。这些改进基于客户反馈和我们自己的经验，并为未来的改进奠定了基础。

用于 Windows 的 .NET Core SDK 安装程序

让我们从 .NET Core SDK 安装程序开始。

安装程序会删除以前的版本

从 .NET Core 3.0 Preview 7 开始，.NET Core SDK 安装程序将在成功安装后删除以前的程序版本。这意味着，如果您在计算机上具有 3.0 Preview 5 和 Preview 7，然后安装 Preview 7，则该过程完成后仅保留Preview 7。

在此步骤的进度对话框中，您将看到"处理：以前的版本"。

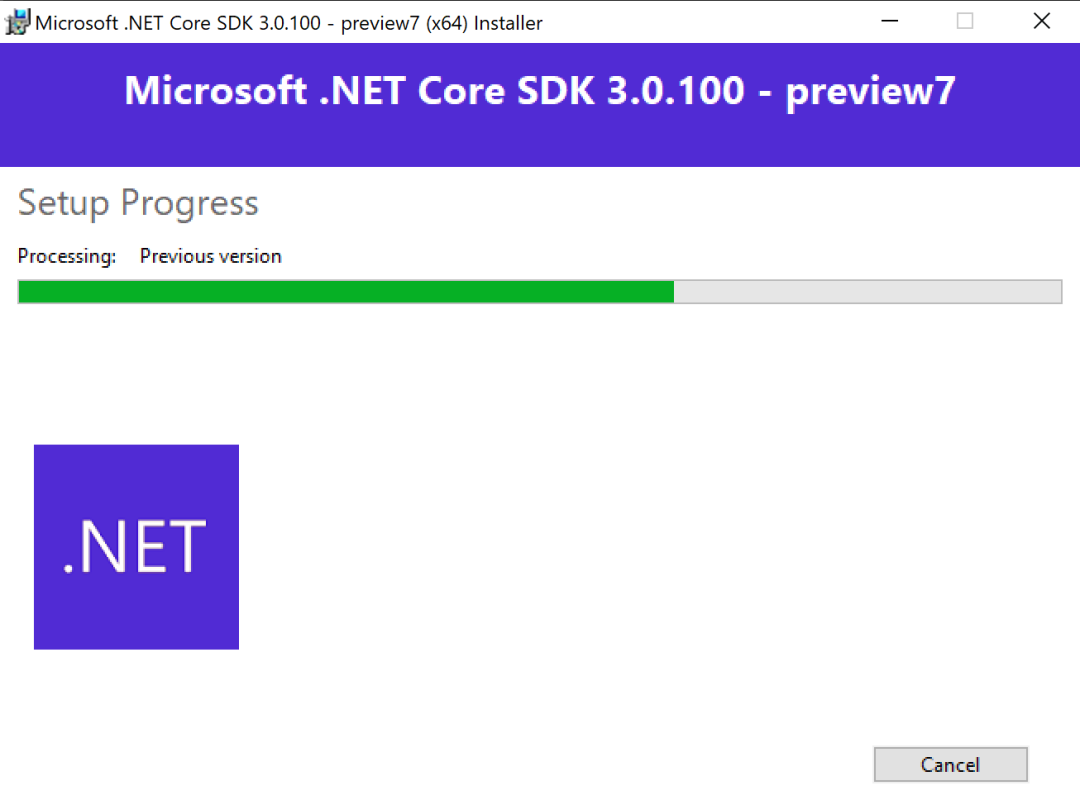
如果您想了解更多，请参阅 .NET Core 如何进行版本化概述。

https://docs.microsoft.com/en-us/dotnet/core/versions/

删除以前的修补程序版本的更改是基于客户对可能在计算机上累积的许多已安装版本的反馈进行的。

安装早期版本的 .NET Core

.NET Core 仍支持并行安装。.NET Core 以前发布的所有版本均可在 .NET Core 下载页面下载。您可以使用 dotnet -info 找出您的计算机上哪些 .NET Core SDK 和运行时。

Visual Studio 中的 .NET Core 安装

Visual Studio 2019 16.3 Preivew 1 包括 .NET Core 安装的以下改进。

我们已迁移到一个模型，其中每个 Visual Studio 安装都将有一个 SDK。可以安装多个版本的运行时，使您能够使用当前 SDK 定位运行时的较低版本。

Visual Studio 现在删除以前的 .NET Core 版本

Visual Studio 安装 .NET Core。同样，如果更新或卸载 Visual Studio，.NET Core 也将更新或卸载。

可以根据需要并行下载和安装 .NET Core 和 .NET Core SDK 的其他版本。

Windows .NET Core 安装程序安装的任何 .NET Core 版本都不受 Visual Studio 安装程序的影响。例如，如果如上文所述安装 .NET Core 的其他版本，就会发生这种情况。

程序和功能控制面板中的 .NET Core

Visual Studio 现在负责其 .NET Core 的副本。Visual Studio 安装的 .NET Core 版本再程序和功能控制面板中将不会有条目。

Visual Studio 和 .NET Core 安装程序将继续使用相同的根目录 C:\Program Files\dotnet。请务必不要删除 dotnet 目录，因为Visual Studio 依赖于该位置的 .NET Core。如果通过删除 dotnet 目录而破坏了Visual Studio，请在 Visual Studio 安装程序中运行"修复"。

.NET Core 的 Visual Studio 负载

安装程序工作负载选择具有与以前版本的 Visual Studio 相同的体验。当选择需要 .NET Core 的工作负载时，将安装 3.0 开发工具 （SDK） 和 3.0 运行时。

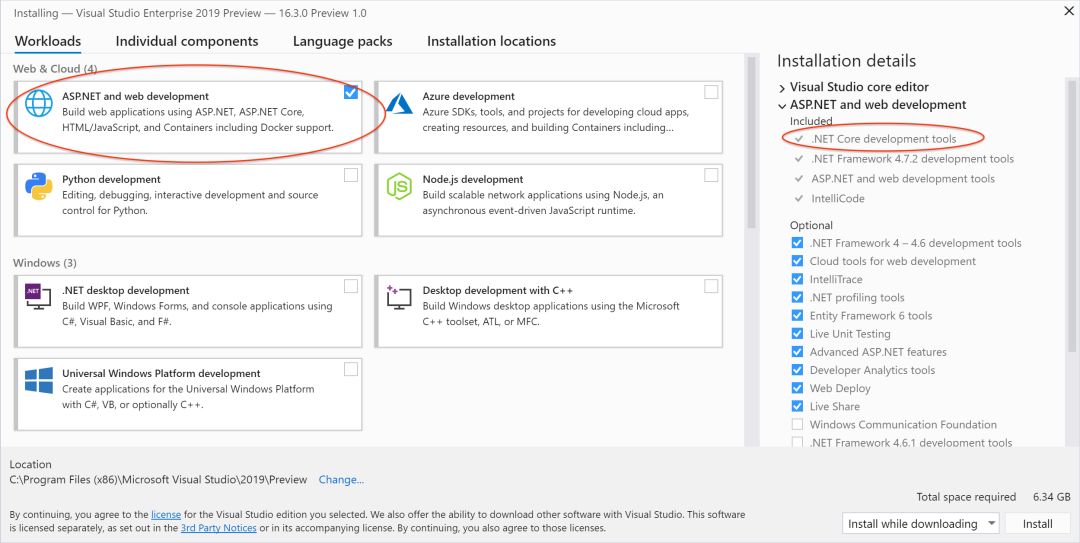
添加 .NET Core 2.1 或 2.2

.NET Core 2.1 和 2.2 是 Visual Studio 2019 16.3 中的可选组件，需要在"单个组件"选项卡中显式选择。

如果您已经安装了 .NET Core 2.1 和/或 2.2 SDK，则应用程序无需执行其他操作即可定位这些版本。即使您可能安装了 .NET Core 2.1 或 2.2，但"Visual Studio 安装程序单个组件"选项卡也不会选择这些组件。如果要确保您拥有最新的 .NET Core 2.1 或 2.2，请在"单个组件"选项卡中选择它们。

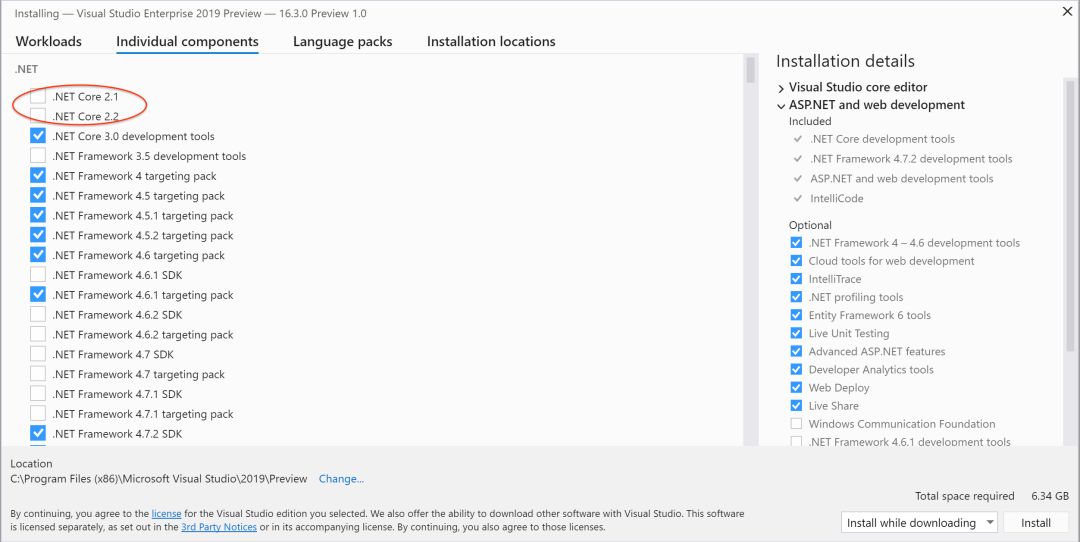
在 Visual Studio 16.3 的更高版本中，只要选择 .NET Core 工作负载，就会安装 .NET Core 3.0 和 2.1（这是长期支持或 LTS 版本）。

未来的增强功能

我们正在考虑对 .NET Core 安装程序进行其他增强。我们正在为即将发布的版本探索的功能类型包括：

• 针对 Mac 安装程序的 Visual Studio 和适用于 Mac 的 .NET Core 安装程序的类似改进和增强功能。

• 用于管理 .NET Core 的全功能 Windows 安装程序。

• 发现和安装更新的功能，类似于 Visual Studio 安装程序中的更新通知。

• 一种删除工具，用于轻松管理 .NET Core 的多个实例，这些实例可能位于计算机上。

如果还有其他想让我们考虑的安装程序建议，请发表评论。