来源：https://www.cnblogs.com/7tiny/p/11348785.html

【前言】

本系列主要讲述sonarqube的安装部署以及如何集成jenkins自动化分析.netcore项目。目录如下：

1. SonarQube系列一、Linux安装与部署

2. SonarQube系列二、分析dotnet core/C#代码

3. SonarQube系列三、Jenkins集成SonarQube（dotnetcore篇）

【实现功能】

　　这篇文章将要介绍的主要内容如下：

1. 将上一篇文章中的sonarqube命令整合为shell脚本

2. 将 shell 脚本集成到jenkins中

【整合sonarqube命令为shell脚本】

因为使用的是 linux 服务器，因此，我们将上一篇文章中关于 sonarqube 的相关命令整合到 shell 脚本中，以便方便地调用，并且很容易集成到CI/CD工具中。

shell 脚本另一个优势就是不需要在 jenkins 上安装过多的插件，而改用脚本调用，保持jenkins的单一整洁，在机器迁移的情况下会异常方便快捷。

1.整合 dotnet test 命令

首先将 dotnet test 命令整合成一个脚本，脚本如下：

#是否执行当前脚本	
execute=$1	
#test项目全路径	
testDir=$2	if [ ${execute} == false ];then	echo "7tiny: There is nothing to execute!"	exit 0	
fi	echo "7tiny:begin test..."	#使用这个方法需要在test项目里安装nuget包：dotnet add package coverlet.msbuild	
dotnet test ${testDir} --logger:"trx;LogFileName=test.trx" /p:CollectCoverage=true /p:CoverletOutputFormat=opencover /p:CoverletOutput='./TestResults/'	if [ $? != 0 ];then	exit 1	
fi	echo "7tiny:test finished!"	exit 0

 参数：

• execute：是否执行脚本（便于和jenkins的checkbox结合，如不需要传true即可）

• testDir：test项目 xxxtexst.csproj 文件完整目录地址

2.整合 dotnet sonarscanner 命令

#是否执行当前脚本	
execute=$1	
#要构建的解决方案名称	
solutionName=$2	
#.sln文件全路径	
solutionDir=$3	if [ ${execute} == false ];then	echo "7tiny: There is nothing to execute!"	exit 0	
fi	echo "7tiny:begin scanner..."	export PATH=${PATH}:${HOME}/.dotnet/tools	dotnet sonarscanner begin /k:${solutionName} /n:${solutionName} /v:${BUILD_NUMBER}	if [ $? != 0 ];then	exit 1	
fi	dotnet build ${solutionDir}	if [ $? != 0 ];then	exit 1	
fi	dotnet sonarscanner end	if [ $? != 0 ];then	exit 1	
fi	echo "7tiny:scanner finished!"	exit 0

 参数：

• execute：是否执行脚本（便于和jenkins的checkbox结合，如不需要传true即可）

• solutionName：要构建的解决方案名称

• solutionDir：.sln文件全路径

脚本里面默认将解决方案的名称当作 sonarqube 中的项目名称；将 jenkins 编译的版本号当作 sonarqube 的活动编号；

3.将shell脚本到服务器 jenkins 可以访问的目录

我们将上述两个 shell 脚本存为 xxx.shell 并存放到服务器上，以便使用 jenkins 调用执行，比如我这里将两个文件存到了服务器某位置：

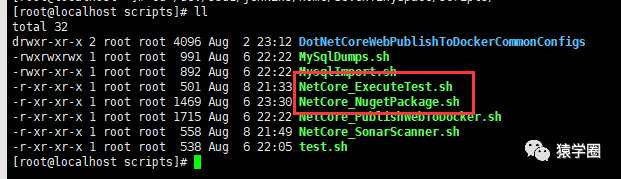
【将shell脚本整合到jenkins中】

有了shell 脚本，那么 jenkins 的整合便非常容易了，我们只需要在 jenkins 的 shell 命令框调用写好的 shell 脚本， 并将参数传递进去即可。

例如：

打开 jenkins 中的的某个项目的项目配置：

然后在最下面的 Build 区域 Execute Shell 框内填写相应的 shell 命令，当然是调用我们的 shell 脚本：

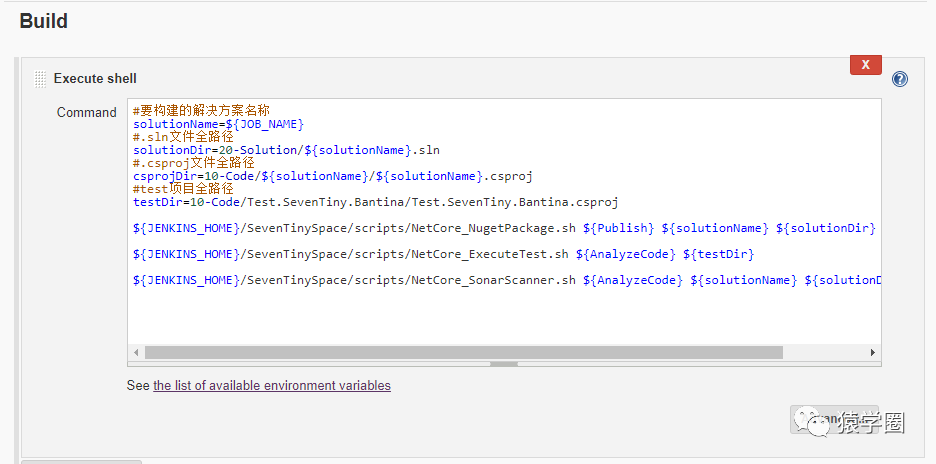
依次调用了：

1. 编译打包发布nuget

2. 执行test

3. 执行sonar canner

每个脚本的第一个参数都是是否执行，以便于我们配置 checkbox 决定是否执行某个脚本，其他参数按顺序传入即可。

checkbox 的配置方式：

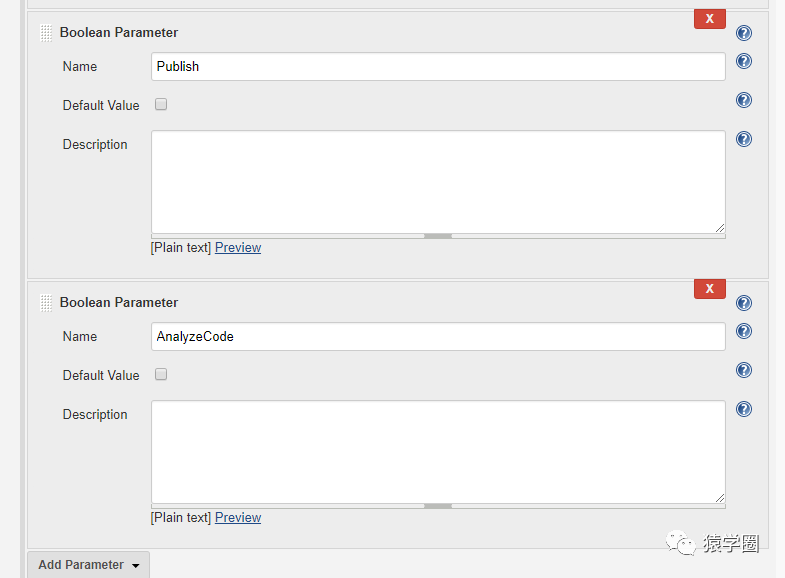
【Jenkins编译执行代码分析】

我们本次不进行nuget打包，只进行代码分析，因此选择代码分析的 checkbox ：

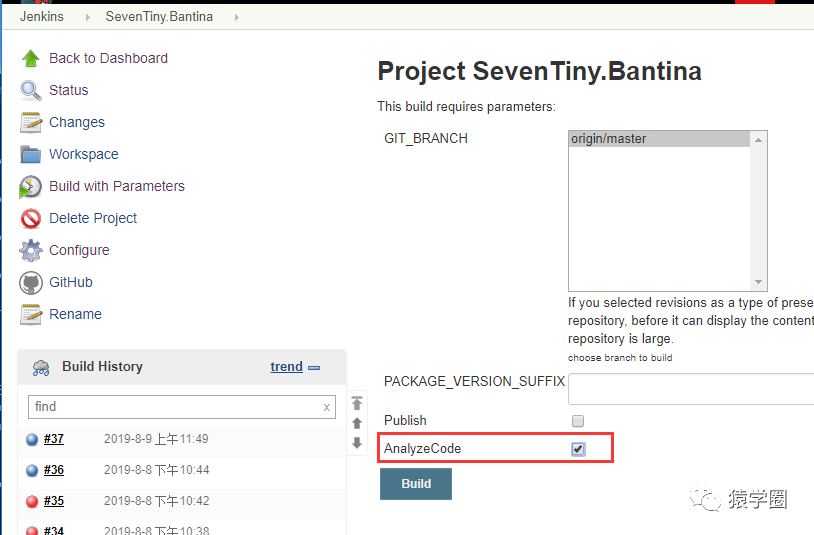
点击 Build 然后静候执行的结果，通过 jenkins 的日志，我们可以看出代码分析结果已经成功推送到了 sonarqube。

我们可以打开 sonarqube 的对应项目进行查看：

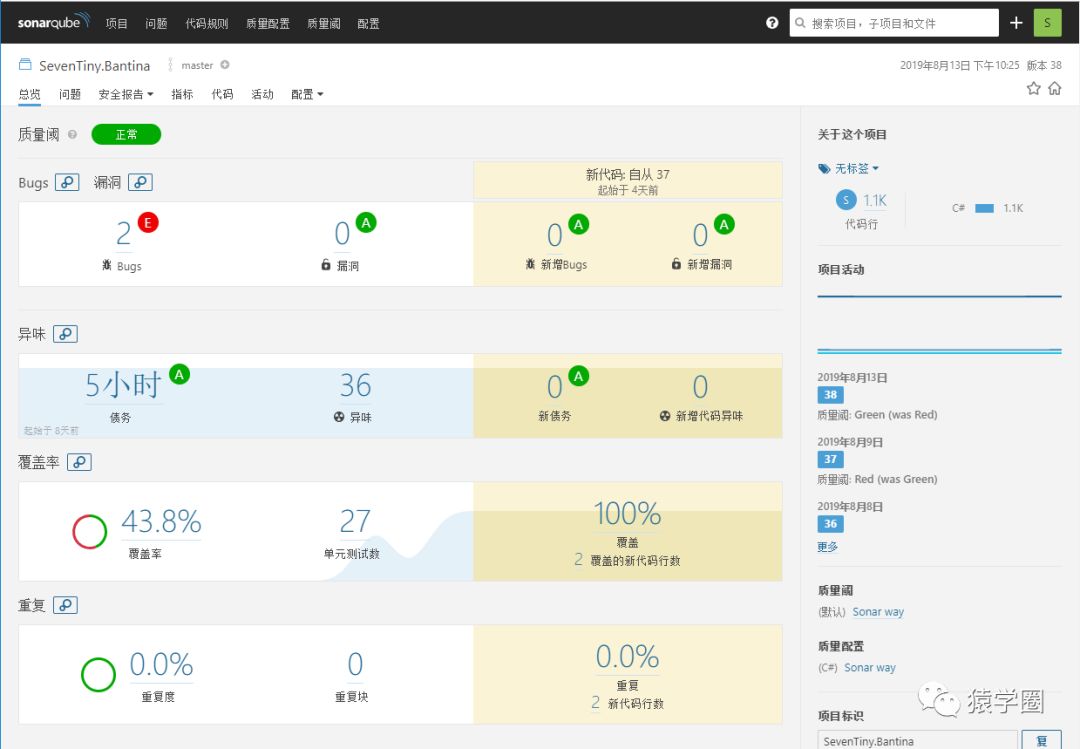
通过结果我们可以看出，本次构建相对于上次构建的结果，新加的代码的单元测试覆盖达到了百分百，且没有任何代码不规范和漏洞，但是历史的代码还有很多的漏洞需要填补。

【总结】

使用 sonarqube 分析dotnet core/C#代码的全部过程以及集成jenkins已经完成了，通过通用的脚本，我们可以方便地应用到多个项目中。

-END-

---

点个赞，让我在心里记住你 ☟