常用的集成学习策略

在之前的文章我有介绍过常用的基本决策树模型ID3、C4.5、CART算法，其中提到了一个关于基本决策树模型的缺点，那就是决策树模型学习一棵最优的决策树被认为是NP-Complete问题。实际中的决策树是基于启发式的贪心算法建立的，这种算法不能保证建立全局最优的决策树，Random Forest 引入随机能缓解这个问题。

那么什么是Random Forest呢？其实这正是今天首先要介绍的集成学习框架的一种，常见的集成学习框架有三种：Bagging，Boosting 和 Stacking。三种集成学习框架在基学习器的产生和综合结果的方式上会有些区别，其中Stacking用的不是特别多，仅做简单了解即可。

下面我会详细介绍Bagging和Boosting的集成思想和对应的集成框架，但是不包括它们的推导，至于它们的公式推导我会在会另外用一篇博文进行详细介绍。

1.Bagging

Boosting是一簇可将基学习器提升为强学习器的算法。每个基学习器都会对训练集进行有放回抽样得到子训练集，比较著名的采样法为 0.632 自助法。每个基学习器基于不同子训练集进行训练，并综合所有基学习器的预测值得到最终的预测结果。Bagging 常用的综合方法是投票法，票数最多的类别为预测类别。

2.Boosting

Boosting 训练过程为阶梯状，基模型的训练是有顺序的，每个基模型都会在前一个基模型学习的基础上进行学习，最终综合所有基模型的预测值产生最终的预测结果，用的比较多的综合方式为加权法。

3.Stacking

Stacking 是先用全部数据训练好基模型，然后每个基模型都对每个训练样本进行的预测，其预测值将作为训练样本的特征值，最终会得到新的训练样本，然后基于新的训练样本进行训练得到模型，然后得到最终预测结果。

总结：

上面介绍的三种集成学习思想，都可以改善基本决策树模型的贪心算法得到的不是最优解的问题。并且我们可能常听到这样一种说法：

• bagging是减少方差（variance）
• boosting是减少偏差（bias）

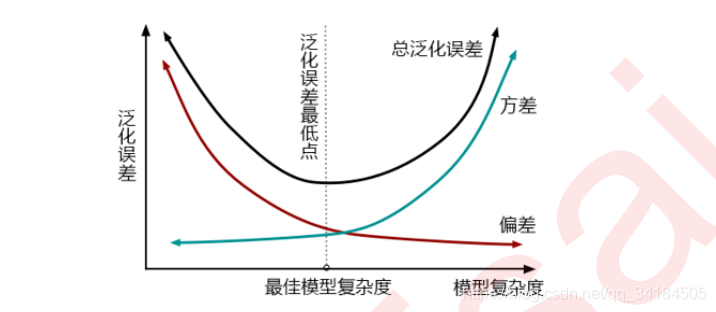
**偏差：**可以简单的理解为“ 准度 ”，与目标值得距离越远偏差越大。减小偏差需要增加模型得参数，但又易过拟合。
**方差：**可以简单得理解为“ 稳度 ”，分散程度越高方差越大（叶子节点多）。减小方差需要加少模型参数，但又易欠拟合。

需要注意得是，我们常说的集成学习的基模型与弱模型本不是一回事。集成学习的基模型可能是“弱模型”也可能是“强模型”。

• 通常来说弱模型是偏差高（在训练集上准确度低）方差小（防止过拟合能力强）的模型。
• 强模型是指偏差低，方差高的模型，也就是准确度高，但是可能过拟合的模型

综上所述：
对于 Bagging 来说，整体模型的偏差与基模型近似，而随着模型的增加可以降低整体模型的方差，故其基模型需要为强模型；（偏差低，方差高）准确率高，但是可能有一点过拟合。

对于 Boosting 来说，整体模型的方差近似等于基模型的方差，而整体模型的偏差由基模型累加而成，故基模型需要为弱模型。（偏差高，方差低）准确率低，但是并没有过拟合。

常用的集成框架

1.Random Forest

Random Forest（随机森林）是 Bagging 阵容的一员，很多人一听到随机森林就把重点放在“森林”两个字上面了，简单地认为随机森林就是很多棵决策树组合投票，却忽略了森林前面的重要修饰“随机”。

集成思想：

随机森林是 Bagging 的扩展变体，它在以决策树为基学习器构建 Bagging 集成的基础上，进一步在决策树的训练过程中引入了随机特征选择，因此可以概括 RF 包括四个部分：

1. 随机选择样本（放回抽样）；
2. 随机选择特征；
3. 构建决策树；
4. 随机森林投票（平均）。

优点：

1. 随机的思想，使得每课树即使不剪枝也不容易过拟合；
2. 在数据集上表现良好，相对于其他算法有较大的优势；
3. 易于并行化，在大数据集上有很大的优势；
4. 能够处理高维度数据，不用做特征选择。

2.Adaboost

AdaBoost（Adaptive Boosting，自适应增强）是Boosting阵容的一员，其自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器。同时，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。

集成思想：

1. 初始化训练样本的权值分布，每个样本具有相同权重；
2. 训练弱分类器，如果样本分类正确，则在构造下一个训练集中，它的权值就会被降低；反之提高。用更新过的样本集去训练下一个分类器；
3. 将所有弱分类组合成强分类器，各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，降低分类误差率大的弱分类器的权重。

Adaboost 模型是加法模型，学习算法为前向分步学习算法，损失函数为指数函数的分类问题，为了防止 Adaboost 过拟合，我们通常也会加入正则化项，这个正则化项我们通常称为步长（learning rate）。对于前面的弱学习器的迭代。

加法模型：最终的强分类器是由若干个弱分类器加权平均得到的。

前向分布学习算法：算法是通过一轮轮的弱学习器学习，利用前一个弱学习器的结果来更新后一个弱学习器的训练集权重。

优点

1. 分类精度高；
2. 可以用各种回归分类模型来构建弱学习器，非常灵活；
3. 不容易发生过拟合。

缺点

• 对异常点敏感，异常点会获得较高权重。

3.GBDT

GBDT（Gradient Boosting Decision Tree，梯度提升决策树）是Boosting阵容的一员，它是一种迭代的决策树算法，该算法由多棵决策树组成。GBDT 是被公认的泛化能力较强的算法。

集成思想：

GBDT通过多轮迭代,每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的梯度（如果损失函数最小均方损失函数（MSE），则负梯度就是残差值）基础上进行训练。对弱分类器的要求一般是足够简单，并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度。

GBDT主要由三部分组成：1.Gradient Boosting（GB）也就是梯度提升、2.Decision Tree（DT，这里用的是回归树）、3.Shrinkage（一个重要思想）

回归树 Regression Decision Tree

GBDT中的弱分类器选择的是CART回归树，而并不是分类树（虽然调整后也可以分类）。对于分类树而言，其值加减无意义（如性别），而对于回归树而言，其值加减才是有意义的（如说年龄）22岁=16岁+4岁+2岁。GBDT 的核心在于累加所有树的结果作为最终结果，所以 GBDT 中的树都是回归树，不是分类树，这一点相当重要。

回归树在分枝时会穷举每一个特征的每个阈值以找到最好的分割点，衡量标准是最小化均方误差。

注意：GBDT用于分类问题仍然使用CART回归树，使用softmax进行概率映射，然后对概率的残差进行拟合

梯度迭代 Gradient Boosting

让损失函数沿着梯度方向的下降。这个就是GBDT中GB的核心。GBDT 每轮迭代的时候，都去拟合损失函数在当前模型下的负梯度。（如果损失函数使用的是平方误差损失函数，则这个损失函数的负梯度就可以用残差来代替，以下所说的残差拟合，便是使用了最小均方损失函数**（MSE）**）

Boosting思想：
GBDT 的 Boosting 不同于 Adaboost 的 Boosting，GBDT 的每一步残差计算其实变相地增大了被分错样本的权重，而对与分对样本的权重趋于 0，这样后面的树就能专注于那些被分错的样本。

缩减 Shrinkage

Shrinkage 的思想认为，每走一小步逐渐逼近结果的效果要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它并不是完全信任每一棵残差树。

加上Shrinkage之前：

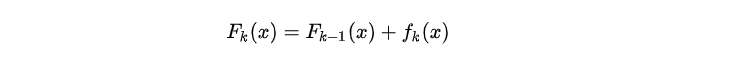
加上Shrinkage之后：

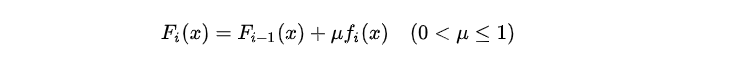
Shrinkage 不直接用残差修复误差，而是只修复一点点，把大步切成小步。本质上 Shrinkage 为每棵树设置了一个 weight，累加时要乘以这个 weight，当 weight 降低时，基模型数会配合增大。

优点：

1. 可以自动进行特征组合，拟合非线性数据；
2. 可以灵活处理各种类型的数据。

缺点：

• 对异常点敏感。

参考文献

https://zhuanlan.zhihu.com/p/86263786