XGBoost简介
XGBoost(eXtreme Gradient Boosting)是华盛顿大学博士陈天奇创造的一个梯度提升(Gradient Boosting)的开源框架。至今可以算是各种数据比赛中的大杀器,被大家广泛地运用。
之前的文章我已经介绍了GBDT,如果对GBDT原理不太懂的,强烈建议先把GBDT的原理搞清楚再回过头来看XGBoost,接下来我会分上中下三篇文章详细介绍XGBoost,包括目标函数,学习策略,重要超参数,系统设计,优缺点等。
目标函数
我们知道 XGBoost 是由 K 个基模型组成的一个加法运算式:
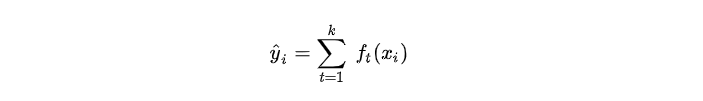
其中fkf_kfk表示第kkk个模型,y^i\widehat{y}_iyi为第iii个样本的预测值。
损失函数可由预测值 y^i\widehat{y}_iyi 与真实值 yiy_iyi 进行表示:
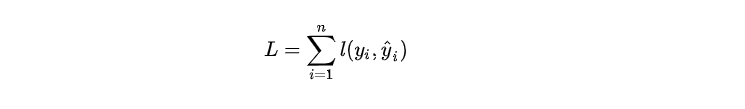
我们知道模型的预测精度由模型的偏差和方差共同决定,损失函数代表了模型的偏差,想要方差小则需要简单的模型,所以目标函数由模型的损失函数 LLL 与抑制模型复杂度的正则项 Ω\OmegaΩ 组成,所以我们有:

Ω\OmegaΩ 为模型的正则项,由于 XGBoost 支持决策树也支持线性模型,所以这里再不展开描述。
我们知道 boosting 模型是前向加法,以第 ttt 步的模型为例,模型对第 iii 个样本 xix_ixi 的预测为:
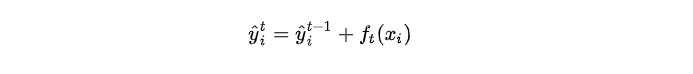
其中 y^it−1\widehat{y}^{t-1}_iyit−1 由第 t−1t-1t−1 步的模型给出的预测值,是已知常数,ft(xi)f_t(x_i)ft(xi) 是我们这次需要加入的新模型的预测值,此时,目标函数就可以写成:
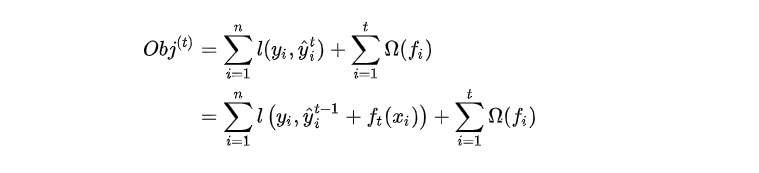
求此时最优化目标函数,就相当于求解 ft(xi)f_t(x_i)ft(xi) 。
根据泰勒公式我们把函数 f(x+Δx)f(x+\Delta x)f(x+Δx) 在点 xxx 处进行泰勒的二阶展开,可得到如下等式:
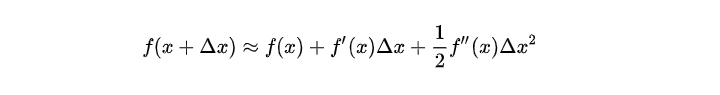
我们把 y^it−1\widehat{y}^{t-1}_iyit−1 视为 xxx, ft(xi)f_t(x_i)ft(xi) 视为 Δx\Delta xΔx ,故可以将目标函数写为:
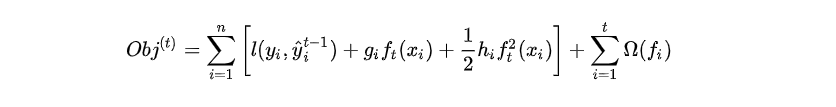
其中 gig_igi 为损失函数的一阶导, hih_ihi 为损失函数的二阶导,注意这里的导是对 y^it−1\widehat{y}^{t-1}_iyit−1 求导。
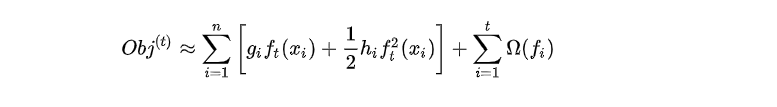
我们以平方损失函数为例:
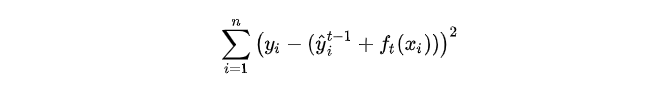
则:
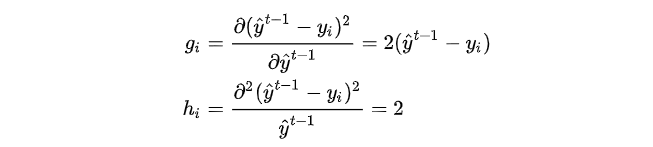
由于在第 ttt 步时 y^it−1\widehat{y}^{t-1}_iyit−1 其实是一个已知的值,所以 l(yi,y^it−1)l(y_i,\widehat{y}^{t-1}_i)l(yi,yit−1) 是一个常数,其对函数的优化不会产生影响,因此目标函数可以写成:

所以我们只需要求出每一步损失函数的一阶导和二阶导的值(由于前一步的 y^t−1\widehat{y}^{t-1}yt−1 是已知的,所以这两个值就是常数),然后最优化目标函数,就可以得到每一步的 f(x)f(x)f(x) ,最后根据加法模型得到一个整体模型。
注意:其实推导到这里我们还可以将上式子进一步简化,式子中的第二项是每个基学习器求和的结果,前面的 t−1t-1t−1 个学习器是已知的,所以正则化的前 t−1t-1t−1 项也是已知的,可以看作一个常数。
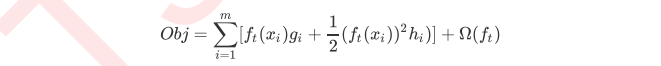
基于决策树的目标函数
我们知道 Xgboost 的基模型不仅支持决策树,还支持线性模型,这里我们主要介绍基于决策树的目标函数。
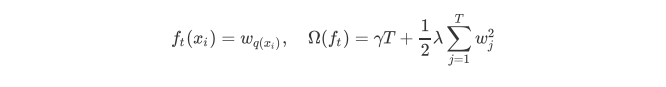 xxx 为某一样本,这里的 q(x)q(x)q(x) 代表了该样本在哪个叶子结点上,而 wqw_qwq 则代表了叶子结点取值 www ,所以 wq(x)w_{q(x)}wq(x) 就代表了每个样本的取值 www(即预测值)。
xxx 为某一样本,这里的 q(x)q(x)q(x) 代表了该样本在哪个叶子结点上,而 wqw_qwq 则代表了叶子结点取值 www ,所以 wq(x)w_{q(x)}wq(x) 就代表了每个样本的取值 www(即预测值)。
决策树的复杂度可由叶子数 TTT 组成,叶子节点越少模型越简单,此外叶子节点也不应该含有过高的权重 www (类比 LR 的每个变量的权重),所以目标函数的正则项可以定义为:
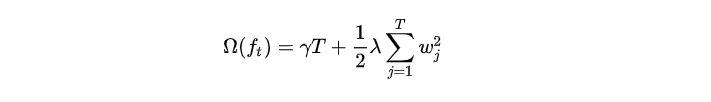
即决策树模型的复杂度由生成的所有决策树的叶子节点数量,和所有节点权重所组成的向量的 L2L2L2 范式共同决定。
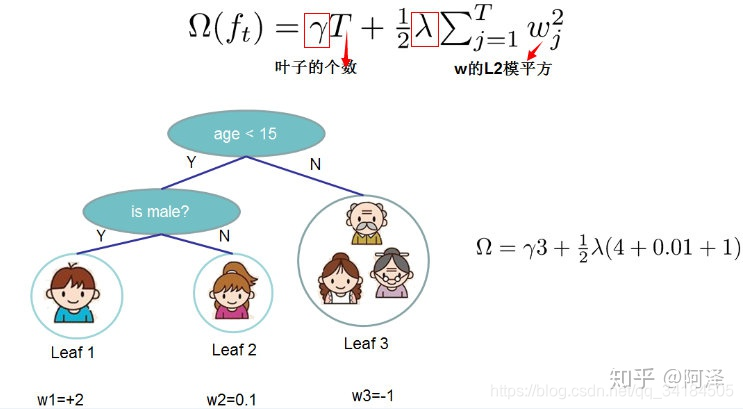
这张图给出了基于决策树的 XGBoost 的正则项的求解方式。
我们设 Ij={i∣q(xi)=j}I_j = \{i\mid q(x_i) = j\}Ij={i∣q(xi)=j} 为第 jjj 个叶子节点的样本集合,故我们的目标函数可以写成:
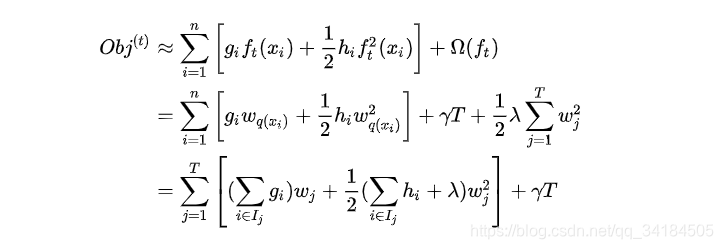
第二步到第三步可能看的不是特别明白,这边做些解释:第二步是遍历所有的样本后求每个样本的损失函数,但样本最终会落在叶子节点上,所以我们也可以遍历叶子节点,然后获取叶子节点上的样本集合,最后在求损失函数。即我们之前样本的集合,现在都改写成叶子结点的集合,由于一个叶子结点有多个样本存在,因此才有了 ∑i∈Ijgi\sum_{i\in I_j}g_i∑i∈Ijgi和 ∑i∈Ijhi\sum_{i\in I_j}h_i∑i∈Ijhi 这两项,wjw_jwj 为第 jjj 个叶子节点取值。
为简化表达式,我们定义 Gj=∑i∈IjgiG_j = \sum_{i\in I_j}g_iGj=∑i∈Ijgi , Hj=∑i∈IjhiH_j = \sum_{i\in I_j}h_iHj=∑i∈Ijhi ,则目标函数为:
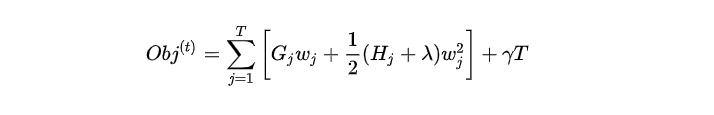
这里我们要注意 GjG_jGj 和 HjH_jHj 是前 t−1t-1t−1 步得到的结果,其值已知可视为常数,只有最后一棵树的叶子节点 wjw_jwj 不确定,那么将目标函数对 wjw_jwj 求一阶导,并令其等于 000 ,则可以求得叶子结点 jjj 对应的权值:
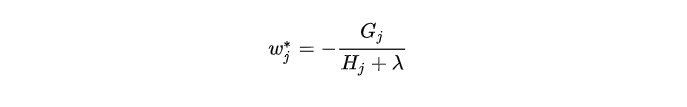
所以目标函数可以化简为:
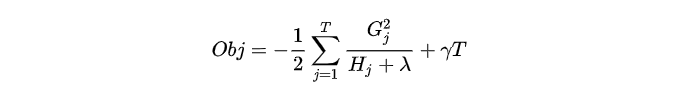
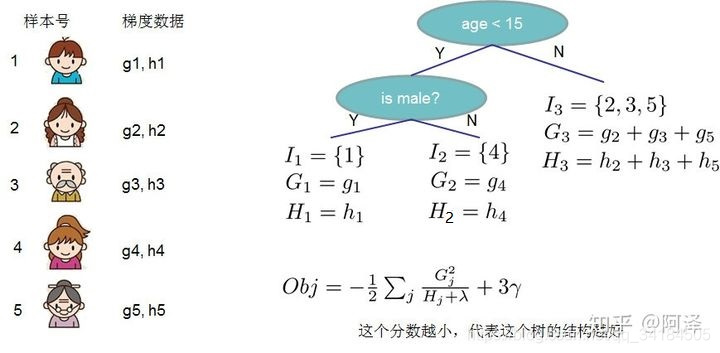
上图给出目标函数计算的例子,求每个节点每个样本的一阶导数 gig_igi 和二阶导数 hih_ihi ,然后针对每个节点对所含样本求和得到的 GiG_iGi 和 HiH_iHi ,最后遍历决策树的节点即可得到目标函数。
到了这里,大家可能已经注意到了,比起最初的损失函数 + 复杂度的样子,我们的目标函数已经发生了巨大变化。我们的样本量已经被归结到了每个叶子当中去,我们的目标函数是基于每个叶子节点,也就是树的结构来计算。所以,我们的目标函数又叫做“结构分数”(structure score),分数越低,树整体的结构越好。如此,我们就建立了树的结构(叶子)和模型效果的直接联系。
最优切分点划分算法
在决策树的生长过程中,一个非常关键的问题是如何找到叶子的节点的最优切分点,Xgboost 支持两种分裂节点的方法——贪心算法和近似算法。
1.贪心算法
贪心算法指的是控制局部最优来达到全局最优的算法,决策树算法本身就是一种使用贪婪算法的方法。XGB作为树的集成模型,自然也想到采用这样的方法来进行计算,所以我们认为,如果每片叶子都是最优,则整体生成的树结构就是最优,如此就可以避免去枚举所有可能的树结构
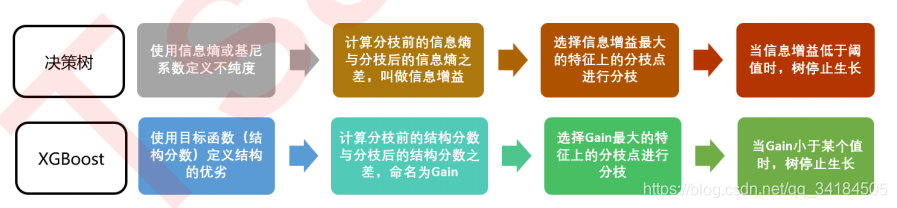
回忆一下决策树中我们是如何进行计算:我们使用基尼系数或信息熵来衡量分枝之后叶子节点的不纯度,分枝前的信息熵与分治后的信息熵之差叫做信息增益,信息增益最大的特征上的分枝就被我们选中,当信息增益低于某个阈值时,就让树停止生长。在XGB中,我们使用的方式是类似的:我们首先使用目标函数来衡量树的结构的优劣,然后让树从深度0开始生长,每进行一次分枝,我们就计算目标函数减少了多少,当目标函数的降低低于我们设定的某个阈值时,就让树停止生长。
具体步骤:
- 从深度为 [公式] 的树开始,对每个叶节点枚举所有的可用特征;
- 针对每个特征,把属于该节点的训练样本根据该特征值进行升序排列,通过线性扫描的方式来决定该特征的最佳分裂点,并记录该特征的分裂收益;
- 选择收益最大的特征作为分裂特征,用该特征的最佳分裂点作为分裂位置,在该节点上分裂出左右两个新的叶节点,并为每个新节点关联对应的样本集
- 回到第 1 步,递归执行到满足特定条件为止
那么如何计算每个特征的分裂收益呢?
假设我们在某一节点完成特征分裂,则分列前的目标函数可以写为:
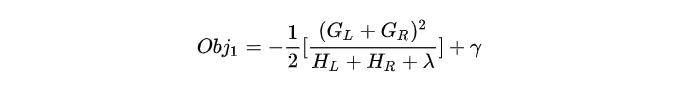
分裂后的目标函数为:
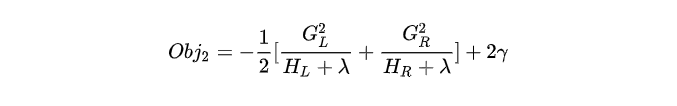
则对于目标函数来说,分裂后的收益为:
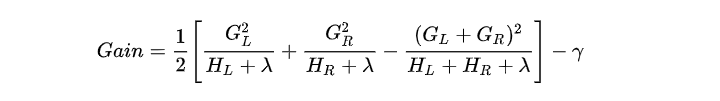
注意该特征收益也可作为特征重要性输出的重要依据。对于每次分裂,我们都需要枚举所有特征可能的分割方案,如何高效地枚举所有的分割呢?
我假设我们要枚举所有 x<ax<ax<a 这样的条件,对于某个特定的分割点 aaa 我们要计算 aaa 左边和右边的导数和。
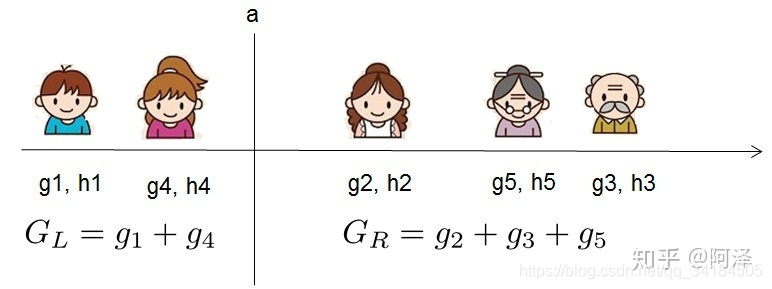
我们可以发现对于所有的分裂点 aaa ,我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和 GLG_LGL 和 GRG_RGR 。然后用上面的公式计算每个分割方案的分数就可以了。
CART树全部是二叉树,因此这个式子是可以推广的。从这个式子我们可以总结出,其实分枝后的结构分数之差为:

其中 GLG_LGL 和 HLH_LHL 从左节点上计算得出, GRG_RGR 和 HRH_RHR 从右节点上计算得出,而 (GL+GR)(G_L + G_R)(GL+GR) 和 (HL+HR)(H_L + H_R)(HL+HR) 从中间节点上计算得出。对于任意分枝,我们都可以这样来进行计算。
在现实中,我们会对所有特征的所有分枝点进行如上计算,然后选出让目标函数下降最快的节点来进行分枝。对每一棵树的每一层,我们都进行这样的计算,比起原始的梯度下降,实践证明这样的求解最佳树结构的方法运算更快,并且在大型数据下也能够表现不错。至此,我们作为XGBoost的使用者,已经将需要理解的XGB的原理理解完毕了。
2.近似算法
贪婪算法可以的到最优解,但当数据量太大时则无法读入内存进行计算,近似算法主要针对贪婪算法这一缺点给出了近似最优解。
对于每个特征,只考察分位点可以减少计算复杂度。
该算法会首先根据特征分布的分位数提出候选划分点,然后将连续型特征映射到由这些候选点划分的桶中,然后聚合统计信息找到所有区间的最佳分裂点。
在提出候选切分点时有两种策略:
Global:学习每棵树前就提出候选切分点,并在每次分裂时都采用这种分割;
Local:每次分裂前将重新提出候选切分点。
直观上来看,Local 策略需要更多的计算步骤,而 Global 策略因为节点没有划分所以需要更多的候选点。
下图给出不同种分裂策略的 AUC 变换曲线,横坐标为迭代次数,纵坐标为测试集 AUC,eps 为近似算法的精度,其倒数为桶的数量。
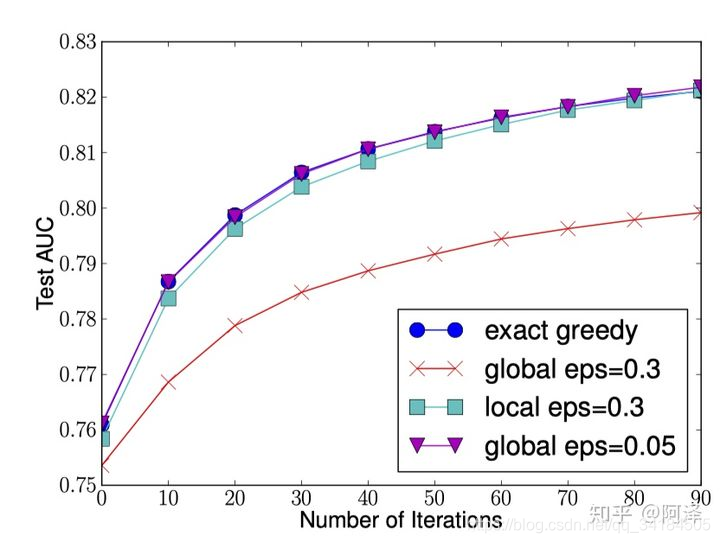
我们可以看到 Global 策略在候选点数多时(eps 小)可以和 Local 策略在候选点少时(eps 大)具有相似的精度。此外我们还发现,在 eps 取值合理的情况下,分位数策略可以获得与贪婪算法相同的精度。

第一个 for 循环:对特征 k 根据该特征分布的分位数找到切割点的候选集合 Sk={sk1,sk2,...,skl}S_k = \{ s_{k1},s_{k2},...,s_{kl}\}Sk={sk1,sk2,...,skl} 。XGBoost 支持 Global 策略和 Local 策略。
第二个 for 循环:针对每个特征的候选集合,将样本映射到由该特征对应的候选点集构成的分桶区间中,即 sk,v≥xjk≥sk,v−1s_{k,v} \geq x_{jk} \geq s_{k,v-1}sk,v≥xjk≥sk,v−1 ,对每个桶统计 G,HG,HG,H 值,最后在这些统计量上寻找最佳分裂点。
下图给出近似算法的具体例子,以三分位为例:
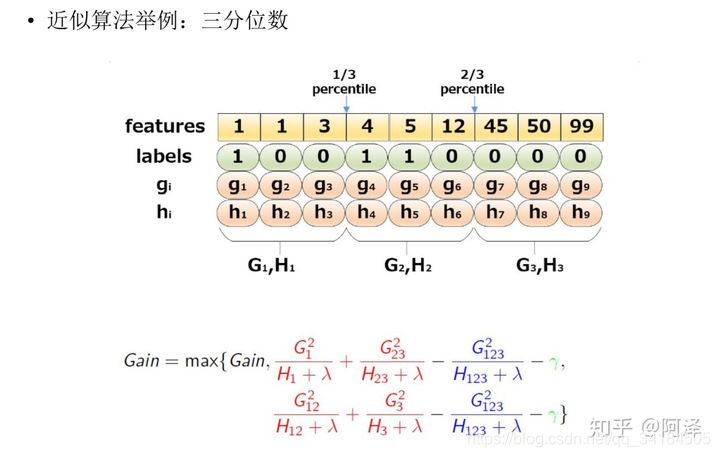
根据样本特征进行排序,然后基于分位数进行划分,并统计三个桶内的 [公式] 值,最终求解节点划分的增益。
加权分位数缩略图
事实上, XGBoost 不是简单地按照样本个数进行分位,而是以二阶导数值 [公式] 作为样本的权重进行划分,如下:
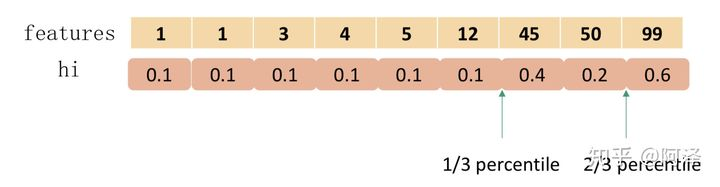
那么问题来了:为什么要用 hih_ihi 进行样本加权?
我们知道模型的目标函数为:
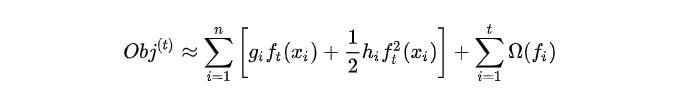
我们稍作整理,便可以看出 hih_ihi 有对 loss 加权的作用。
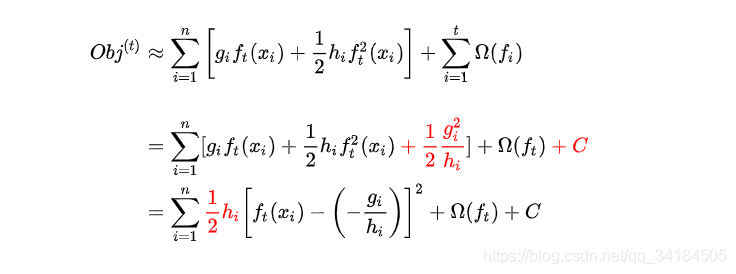
其中 121\over221gi2hig_i^2\over h_ihigi2 与 CCC 皆为常数。我们可以看到 hih_ihi 就是平方损失函数中样本的权重。
对于样本权值相同的数据集来说,找到候选分位点已经有了解决方案(GK 算法),但是当样本权值不一样时,该如何找到候选分位点呢?(作者给出了一个 Weighted Quantile Sketch 算法,这里将不做介绍。)
稀疏感知算法
在决策树的第一篇文章中我们介绍 CART 树在应对数据缺失时的分裂策略,XGBoost 也给出了其解决方案。
XGBoost 在构建树的节点过程中只考虑非缺失值的数据遍历,而为每个节点增加了一个缺省方向,当样本相应的特征值缺失时,可以被归类到缺省方向上,最优的缺省方向可以从数据中学到。至于如何学到缺省值的分支,其实很简单,分别枚举特征缺省的样本归为左右分支后的增益,选择增益最大的枚举项即为最优缺省方向。
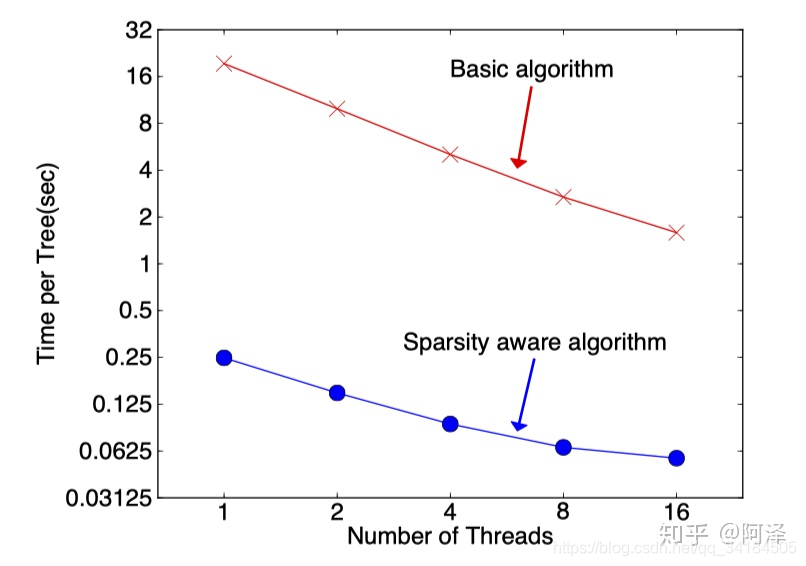
在构建树的过程中需要枚举特征缺失的样本,乍一看该算法的计算量增加了一倍,但其实该算法在构建树的过程中只考虑了特征未缺失的样本遍历,而特征值缺失的样本无需遍历只需直接分配到左右节点,故算法所需遍历的样本量减少,下图可以看到稀疏感知算法比 basic 算法速度块了超过 50 倍。
)
--学习笔记...)
-分治法)
...)





)



- 数据库介绍与基础操作)



- 基础查询语句)
