题目1：
题目描述

输出自然数 1 到 n 所有不重复的排列,即 n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。
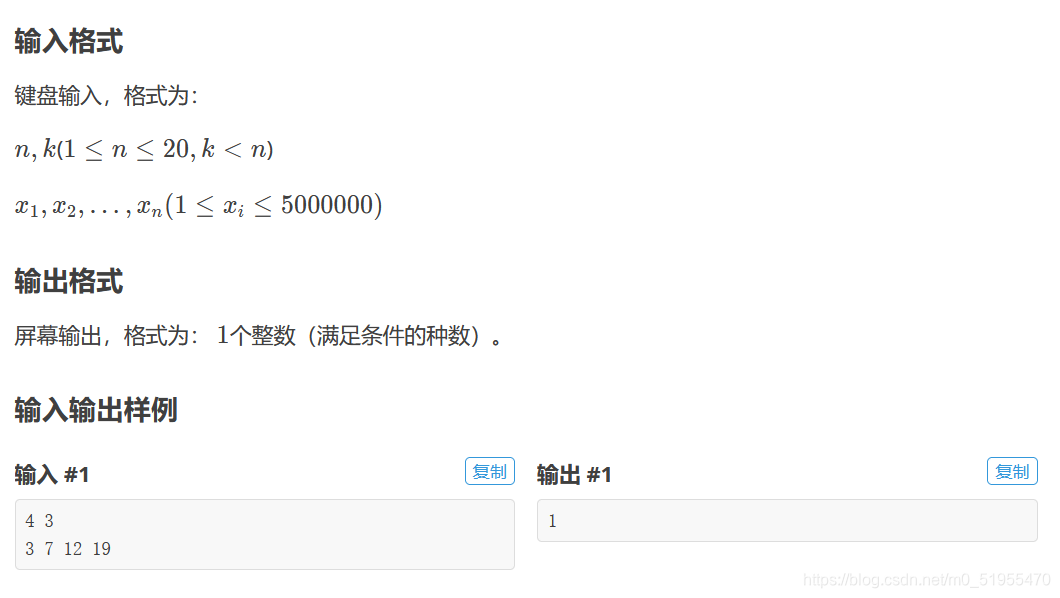
输入格式

一个整数 n。
输出格式

由 $1\sim n$ 组成的所有不重复的数字序列，每行一个序列。

每个数字保留 5 个场宽。
输入输出样例
输入

3

输出

1    2    3
1    3    2
2    1    3
2    3    1
3    1    2
3    2    1

说明/提示

$1\le n\le 9$

代码如下：

#include<bits/stdc++.h> 
using namespace std;
int n;
int ans[15];//保存当前的方案
int use[15];//表示每个数是否被用过
void dfs(int x){//X表示当前搜索到那个数if(x>n){//如果N位都搜索完了，就输出方案并返回for(int i=1;i<=n;i++)printf("% 5d",ans[i]);//输出方案 puts("");return;}for(int i=1;i<=n;i++)//从小到大枚举if(!use[i]){//判断这个数是否用过ans[x]=i;//保存到方案中use[i]=1;//标记这个数被使用了dfs(x+1);//进行下一步搜索use[i]=0;//撤销标记}
}
int main()
{scanf("%d",&n);//输入dfs(1);//从第一个数开始搜索；
}

题目2：

题目描述

已知 nnn 个整数 x1,x2,…,xnx_1,x_2,…,x_nx1​,x2​,…,xn​，以及111个整数kkk(k<nk<nk<n)。从nnn个整数中任选kkk个整数相加，可分别得到一系列的和。例如当n=4,k=3n=4,k=3n=4,k=3,444个整数分别为3,7,12,193,7,12,193,7,12,19时，可得全部的组合与它们的和为：

3+7+12=223+7+12=223+7+12=22

3+7+19=293+7+19=293+7+19=29

7+12+19=387+12+19=387+12+19=38

3+12+19=343+12+19=343+12+19=34。

现在，要求你计算出和为素数共有多少种。

例如上例，只有一种的和为素数：3+7+19=293+7+19=293+7+19=29。

解题思路：
水题！！！

代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N = 9999;
int a[N];
bool pd[N];
int haif[N];
int n, k, sum = 0, ans = 0;int f (int y) {if (y == 1)return false;if (y == 0)return false;for (int i = 2; i <= sqrt(y); i++) {if (y % i == 0)return false;}return y;
}void dfs (int x, int d) {if (x == k + 1) {sum = 0;for (int i = 1; i <= k; i++) {sum = sum + haif[i];}if (f(sum) != 0)ans++;return ;}for (int i = d + 1; i <= n; i++) {if (!pd[i]) {pd[i] = 1;haif[x] = a[i];dfs(x + 1, i);pd[i] = 0;}}
}int main () {cin >> n >> k;for (int i = 1; i <= n; i++) {cin >> a[i];}dfs(1, 0);cout << ans << endl;return 0;
}