递归的概念
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
我会写先介绍递归的基本思想,然后再以后的文章中介绍一下递归的衍生算法,比如:回溯算法、分治法、DFS等。
设计递归的思路
通常我们一提到递归就立马想到了递归的两个重要部分:终止条件与循环部分。递归的设计思路是很像我门做数学题:根据已知条件找规律,利用递推式求解未知变量。但是我们作为开发者面对的是计算机,我们需要用程序语言设计出递归的算法去解决问题。下面是递归设计的四个重要要素:
- 接收的参数
- 返回值
- 终止条件
- 递归拆解:如何递归下一层
递归实例
俗话说的好:”孰能生巧“,光说不练,假把式。光用文字去解释递归如何如何让地去设计,倒不如多花时间从易到难循序渐进做大量练习,通过大量的练习,去寻找其中的规律。
实例1:n的阶乘
# 递归实现N的阶乘
def fact_resursion(n):# 终止条件if n==1:return 1else:return n*fact_resursion(n-1) # 循环部分print(fact_resursion(5))
运行结果:120
实例2:斐波那契数列
这里简单的解释一下斐波那契数列:F(0) = 0 , F(1) = 1
F(N) = F(N-1) + F(N-2) , N>1 数列前几项如下:
0 1 1 2 3 5 8 13 …
# 递归实现斐波那契数列F(N)的计算
def fun(n):# 终止条件if n <=1:return nelse:return fun(n-1) + fun(n-2) # 循环部分
print(fun(8))
运行结果:21
实例3:小青蛙跳台阶
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
解析:
每次跳的时候,小青蛙可以跳一个台阶,也可以跳两个台阶,也就是说,每次跳的时候,小青蛙有两种跳法。
第一种跳法:第一次我跳了一个台阶,那么还剩下n-1个台阶还没跳,剩下的n-1个台阶的跳法有f(n-1)种。
第二种跳法:第一次跳了两个台阶,那么还剩下n-2个台阶还没,剩下的n-2个台阶的跳法有f(n-2)种。
所以,小青蛙的全部跳法就是这两种跳法之和了,即 f(n) = f(n-1) + f(n-2)。至此,等价关系式就求出来了。
def func(n):if n<=2:return nreturn func(n-1) + func(n-2)
print(func(4))
运行结果:5
实例3:列表反转
# 递归实现列表反转
def rev(alist,left,right):if left >= right: # 终止条件returnrev(alist,left+1,right-1)# 循环部分alist[left],alist[right] = alist[right],alist[left]
alist = [1,2,3,4,5,6]
left = 0
right = len(alist) - 1
rev(alist,left,right)
print(alist)
运行结果:[6, 5, 4, 3, 2, 1]
实例4:字符串反转
注意:有人可能会觉得字符串反转和列表反转难道不是一样的吗?
如果用反转列表的方法去反转字符串会出现一下错误:
TypeError: ‘str’ object does not support item assignment
在python中,字符串是不可变对象,不能通过下标的方式直接赋值修改。同样的不可变对象还有:数字、字符串和元组。
直观一点举个小例子:
s = “abcd”
x = s[2]
print(x) => ‘c’
但是直接赋值:s[2] = ‘h’ 却会报错
# 递归实现字符串的反转
def rvs(s):# 终止条件if len(s) == 1:return selse:return rvs(s[1:])+s[0] # 循环部分
print(rvs("abcdefg"))
运行结果:gfedcba
实例5:链表反转
注意:因为实现链表反转需要自己创建一个链表类和方法,比较麻烦我们就直接用leetcode的206题:链表反转。
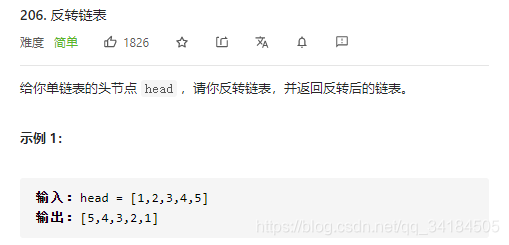
代码:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def reverseList(self, head: ListNode) -> ListNode:# 方法一:双指针# pre,cur = None,head# while cur:# next = cur.next# cur.next = pre# pre = cur# cur = next# return pre# 方法二: 递归# 边界条件 和 终止条件if head == None or head.next == None:return head# 循环部分 newhead = self.reverseList(head.next)head.next.next = headhead.next = Nonereturn newhead
实例6:汉诺塔游戏
汉诺塔问题是一个经典的问题。汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
假设三根柱子分别为:A,B,C。A柱子上有n个盘子,B,C为空。请问每一步该如何移动?
# 汉诺塔
count = 1
n = 4
def move(n,a,b,c):global countif n == 1:print(count,":",a, '-->', c)count += 1else:move(n-1, a, c, b)print(count,":",a, '-->', c)count += 1move(n-1, b, a, c)
print(f'把A柱子的{n}个盘子全部移到C柱子的顺序为:')
move(n, 'A', 'B', 'C')
运行结果:
把把A柱子的4个盘子全部移到C柱子的顺序为:
1 : A --> B
2 : A --> C
3 : B --> C
4 : A --> B
5 : C --> A
6 : C --> B
7 : A --> B
8 : A --> C
9 : B --> C
10 : B --> A
11 : C --> A
12 : B --> C
13 : A --> B
14 : A --> C
15 : B --> C
例子7:科赫雪花
利用python的turtle库绘制科赫雪花,如下图所示:

# 科赫雪花
# -*- coding: utf-8 -*-
import turtle
def koch(size,n):"""函数koch用递归思想绘制一段N阶曲线"""if n == 0:turtle.fd(size) #递归基例(终止条件),0阶曲线即为一条直线else:for i in [0,60,-120,60]: #通过改变方向,绘制四条线段turtle.left(i)koch(size/3,n-1) # 循环部分
def main():"""定义main函数调用koch""" turtle.setup(600,600)turtle.penup()turtle.goto(-250,100)turtle.pendown()turtle.pensize(2)n = 3for i in range(0,3):koch(500,n)turtle.right(120)turtle.hideturtle()turtle.done()
main()
运行结果:




)
)
--学习笔记...)
-分治法)
...)





)



- 数据库介绍与基础操作)
